Für diese Aufgabe benötigst Du folgendes Grundwissen: Mächtigkeit
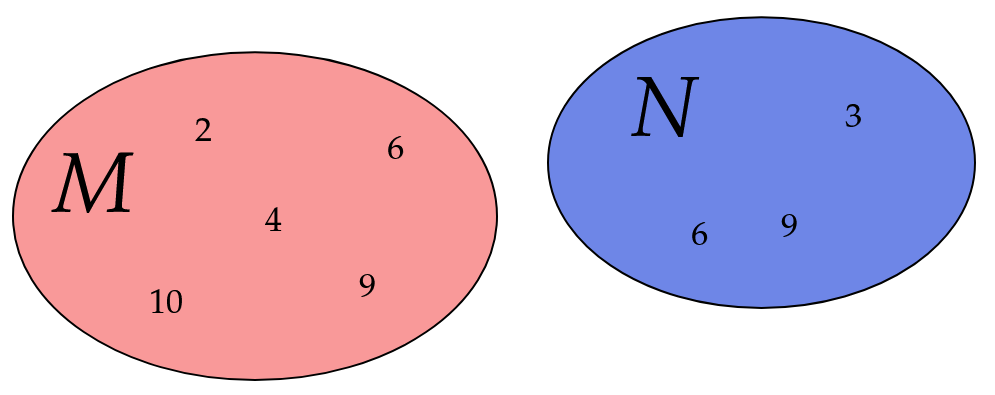
Mächtigkeiten von M und N
M besitzt ∣M∣=5 Elemente. N besitzt ∣N∣=3 Elemente.
Mächtigkeit der Vereinigungsmenge M∪N
Die Vereinigungsmenge besitzt die Elemente M∪N={2,3,4,6,9,10}. Es dürfen keine Elemente doppelt gezählt werden. Damit gilt ∣M∪N∣=6 .
Mit der Rechenregel muss man zuerst die Mächtigkeit von M∩N feststellen: die 6 und die 9 kommen in beiden Mengen vor, daher ist ∣M∩N∣=∣{6;9}∣=2.
Die Rechenregel sagt jetzt:
∣M∪N∣=∣M∣+∣N∣−∣M∩N∣=5+3−2=6, natürlich ist das dasselbe Ergebnis wie beim Abzählen.
Mächtigkeit des kartesischen Produkts M×N
Aufgezählt besteht das kartesische Produkt aus den Elementen
M×N={(2,3);(2,6);(2,9);M×N={(4,3);(4,6);(4,9);M×N={(6,3);(6,6);(6,9);M×N={(9,3);(9,6);(9,9);M×N={(10,3);(10,6);(10,9)}
Damit ist ∣M×N∣=15, sowie auch die Rechenregel ergibt:
∣M×N∣=∣M∣⋅∣N∣=5⋅3=15
