Aufgaben zum Thema Ergebnisraum oder Ergebnismenge
Hier findest du Aufgaben zur Ergebnismenge. Lerne, die Ergebnismenge eines Zufallsexperiments zu erkennen und anzugeben.
- 1
In einer Klinik wird eine Statistik über das Geschlecht von Neugeborenen geführt. Hierbei werden Kinder als weiblich (W), männlich (M) oder als divers (D) einsortiert.
Gib jeweils den Ergebnisraum und die Mächtigkeit an, und zwar bei:
Einzelkindern
Zwillingen, wenn auch die Reihenfolge der Geburt festgehalten wird.
Drillingen, wenn auch die Reihenfolge der Geburt festgehalten wird.
- 2
Münze und Würfel werden gleichzeitig geworfen. Wie lautet ein Ergebnisraum? Wie viele Elemente enthält er?
- 3
Der Gewinner bei einer Lotterie darf aus 5 DVDs (a,b,c,d,e) 3 auswählen. Gib den Ergebnisraum und seine Mächtigkeit an, wenn
beliebig ausgewählt werden darf.
grundsätzlich e gewählt werden muss.
bei Wahl von a stets auch b gewählt werden muss.
- 4
In einer Urne liegen vier mit 1 bis 4 nummerierte Kugeln. Man zieht zwei Kugeln auf einmal. Gib einen Ergebnisraum an!
- 5
Beim Werfen zweier Würfel bietet jemand die folgende Menge als Ergebnisraum an. Entscheide, ob wirklich ein Ergebnisraum vorliegt und gib die Mächtigkeit an.
- 6
Jemand hat drei Lose gekauft. Sie werden in Treffer (T) und Niete (N) unterschieden. Wie lautet der Ergebnisraum , wenn
die drei Lose unterscheidbar sind,
die drei Lose nicht unterschieden werden?
- 7
In den Spielregeln für ein Würfelspiel steht: „Man werfe beide Würfel und bilde aus den beiden oben liegenden Augenzahlen die größtmögliche Zahl.“ (Beispiel: Bei den Augenzahlen „2“ und „4“ ist das die Zahl „42“.)
Gib einen Ergebnisraum für dieses Spiel an.
Gib folgende Ereignisse in Mengenschreibweise an: A: Die gebildete Zahl besteht aus zwei gleichen Ziffern. B: Die Zahl enthält mindestens eine 4. C: Die Einerziffer ist halb so groß wie die Zehnerziffer. D: Die Zahl ist größer als 10. E: Die Quersumme der Zahl ist 6. F: Die Zahl ist eine Primzahl.
Untersuche die Ereignisse A bis F auf paarweise Unvereinbarkeit.
Beschreibe folgende Ereignisse in Worten: G = {11; 21; 22} H = {22; 42; 44; 62; 64; 66}
- 8
Ergebnismenge eines Glücksrads bestimmen
Auf einer Kirmes wird ein Glücksrad gedreht, welches unterschiedliche Farben als Gewinnfelder hat.
Bestimme die Ergebnismenge des Glücksrads.
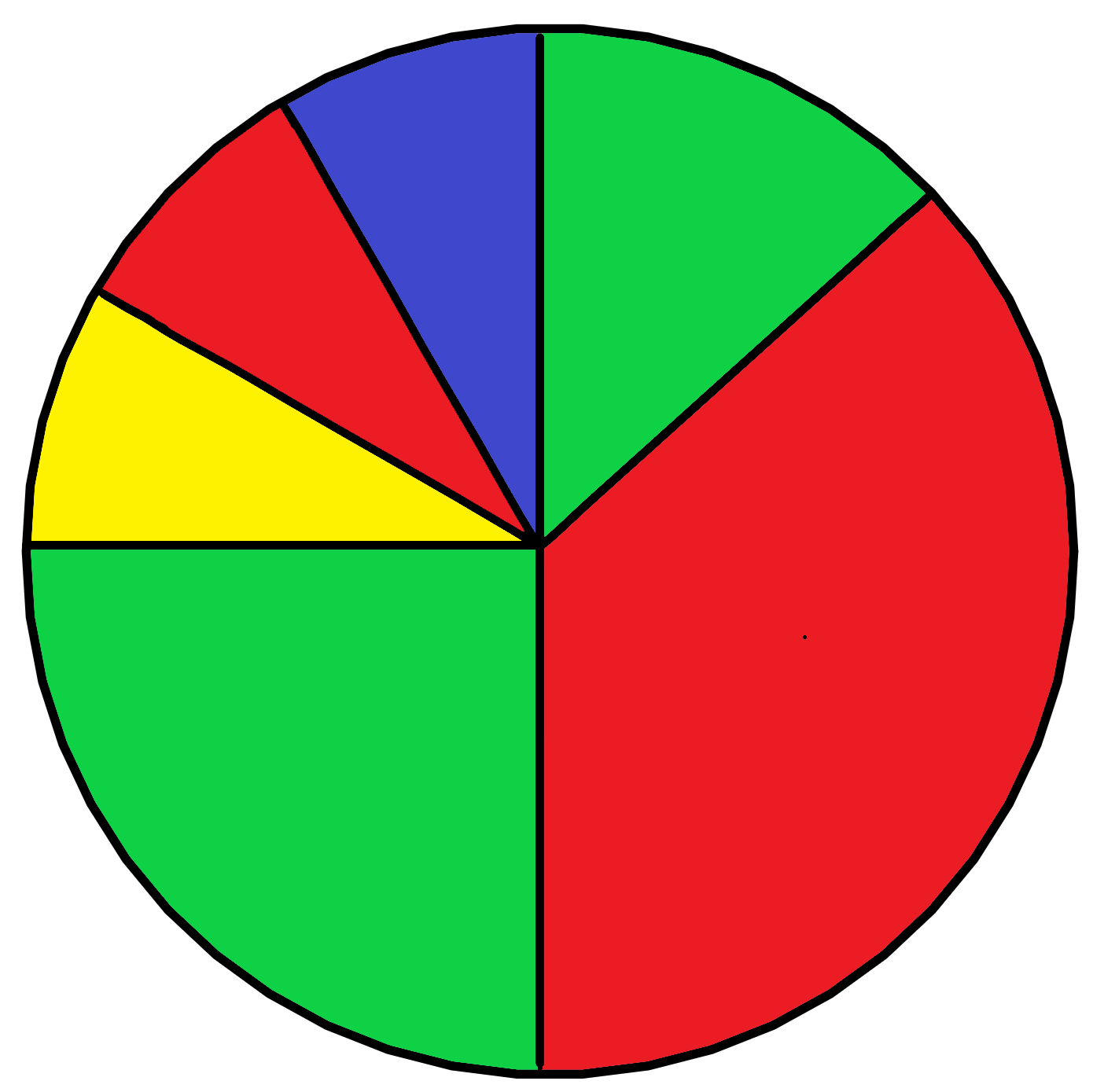
- 9
Mächtigkeit von Mengen
Gib die Mächtigkeiten der Mengen und , sowie und an.
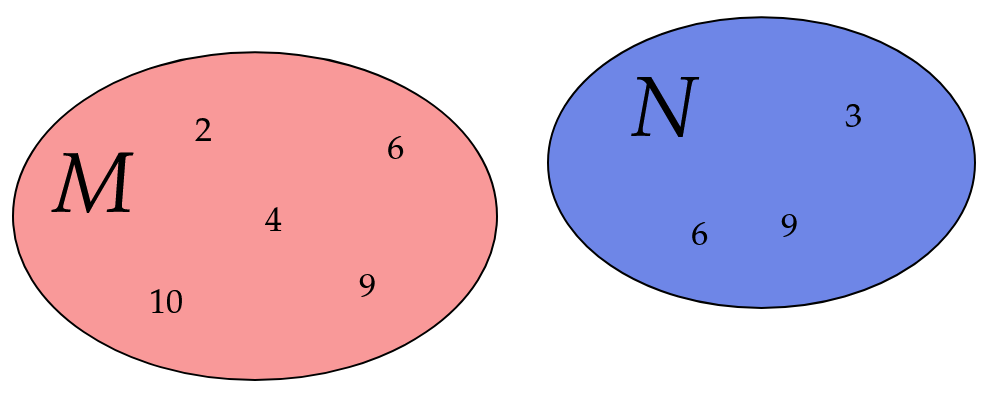
- 10
Gegeben sind
Wie viele Elemente besitzen die Mengen
und
?
- 11
Der Skat-Abend
Ein gewöhnliches Set von Skat-Karten hat 32 Karten. Gebe mindestens vier verschiedene Möglichkeiten von Ergebnisräumen für das Kartenset an.

- 12
3 gleiche Münzen werden gleichzeitig geworfen. Verschiedene Reihenfolge werden nicht unterschieden. Also sind zum Beispiel die Ereignisse und gleich.
Gib einen geeigneten Ergebnisraum an.
Gib die Mächtigkeit des Ereignisraums an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
