Beispiel: Würfel
Beim Mensch-Ärgere-Dich-Nicht muss eine 6 gewürfelt werden, damit man aus dem Haus ziehen darf.
Hier ist 6 das Ereignis und alle anderen Zahlen (1; 2; 3; 4; 5) das Gegenereignis.

Ereignismenge
Wir haben bereits gesehen, dass wir die Ergebnisse eines Zufallsexperiments als Ergebnismenge darstellen können. Genauso können wir auch die Ereignisse als Ereignismenge darstellen. Dafür schreiben wir alle günstigen Ereignisse als Menge .
"Günstig" steht für das in der Aufgabenstellung gesuchte Ereignis.
Beispiel: Würfel
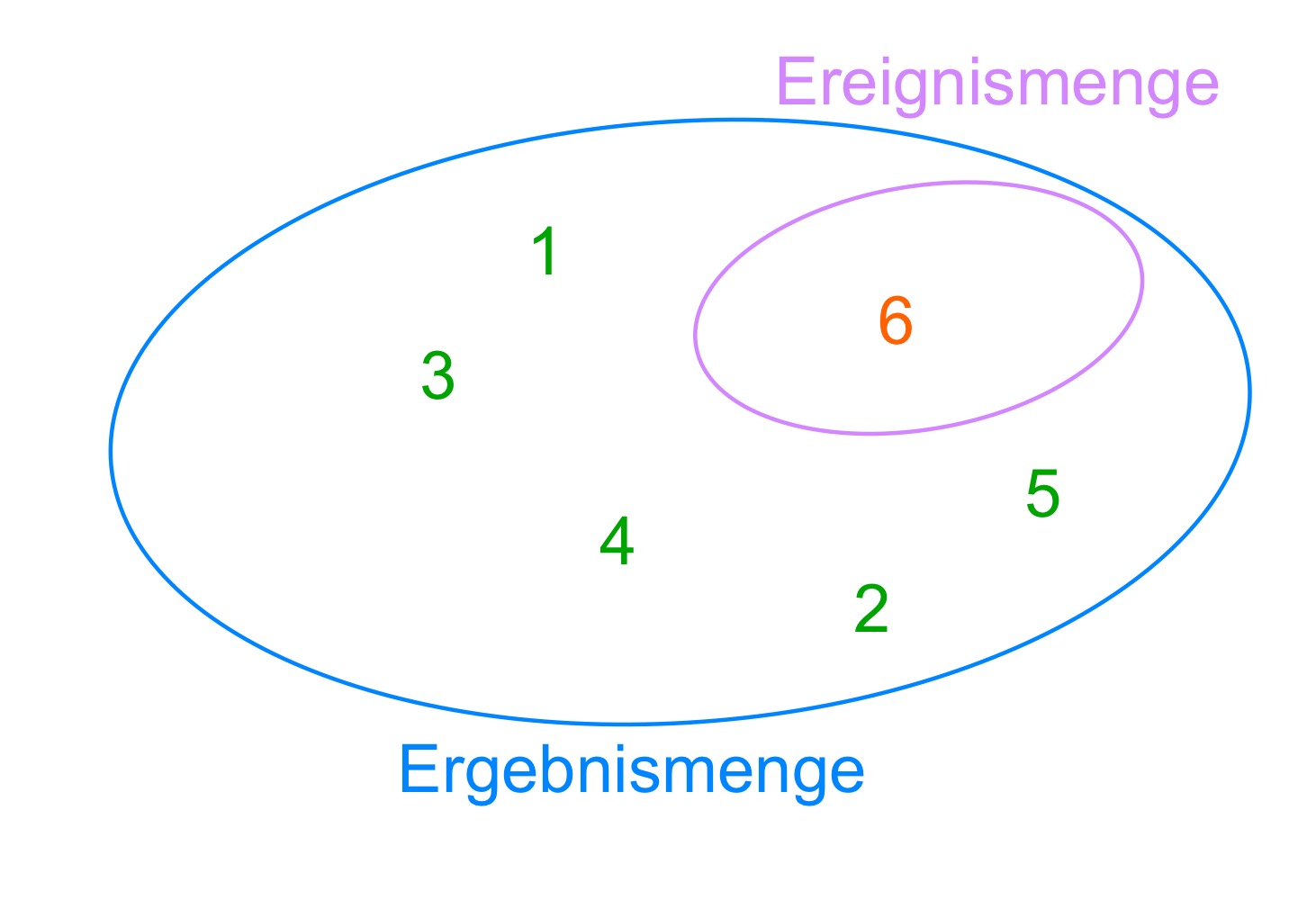
Es gibt sechs mögliche Ausgänge, die Ergebnismenge besteht also aus sechs Elementen:
{1; 2; 3; 4; 5; 6}.
Es gibt ein günstiges Element, die Ereignismenge besteht also aus einem Element:
{6}.
Berechnung der Wahrscheinlichkeit eines Ereignisses
Beispiel: Würfel
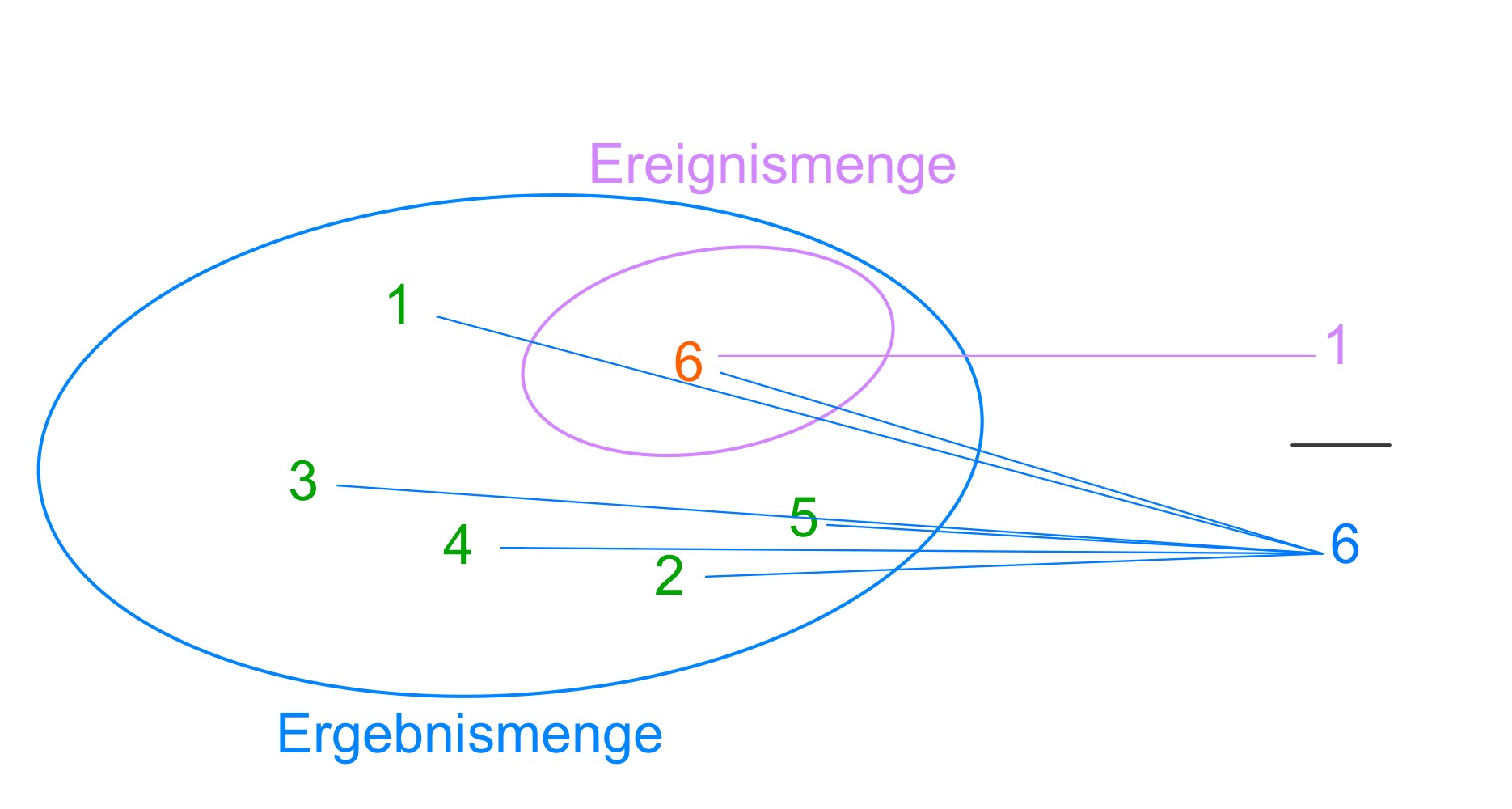
Es gibt einen günstigen Ausgang (6) und sechs mögliche Ausgänge (1; 2; 3; 4; 5; 6).
Die Wahrscheinlichkeit, eine 6 zu würfeln, beträgt also .
Eine ausführliche Erklärung zur Berechnung der Wahrscheinlichkeit findest du im Artikel Laplace-Experiment.
Berechnung der Wahrscheinlichkeit eines Gegenereignisses
Wir haben bereits bei der Ergebnismenge gesehen, dass alle Wahrscheinlichkeiten der Ergebnismenge zusammen immer ergeben. Weil sich die Ergebnismenge aus Ereignis und Gegenereignis zusammensetzt, müssen die Wahrscheinlichkeit des Ereignisses und die Wahrscheinlichkeit des Gegenereignisses zusammen auch ergeben:
Um die Wahrscheinlichkeit des Gegenereignisses zu bekommen, rechnen wir also:
Beispiel: Würfel
Das Gegenereignis ist "keine 6" und die Wahrscheinlichkeit ist:
ALT: Ereignis
Ein Ereignis ist ein Teil der Ergebnismenge . Die Menge im Bild ist eine Teilmenge des Ergebnisraumes beim Würfelexperiment.
Das Ereignis tritt ein, sobald ein Element, also oder gewürfelt wird. Es können auch mehrere Ereignisse gleichzeitig eintreten.

Beispiel zu Ereignissen
Betrachtet wird das Zufallsexperiment "Werfen eines Würfels" mit dem Ergebnisraum
Ereignisse sind zum Beispiel:
A: "Die Augenzahl ist gerade", in Mengenschreibweise:
B: "Die Augenzahl ist größer als 3". In diesem Fall wäre
Wenn nun z. B. eine 2 gewürfelt wird, ist A eingetreten, nicht aber B. Wenn eine 6 gewürfelt wird, sind sowohl A als auch B eingetreten.
Nicht jedes Ereignis muss eine "sinnvolle" Interpretation (wie "Augenzahl gerade" oder "Augenzahl größer als 3") haben.
Jede beliebige Teilmenge von ist ein Ereignis, ob man ihm nun einen "Sinn" zuschreiben kann oder nicht.
Darstellung in verschiedenen Schreibweisen
Ein Ereignis kann sowohl als Menge, als auch als Wortformulierung angegeben werden. Die Schreibweisen
und
: "Die Augenzahl ist gerade" bzw.
: "Die Augenzahl ist größer als 3".
sind hierbei vollkommen identisch für die Ereignisse und . Wenn in Aufgaben nach Interpretationen von Ereignissen gefragt wird, ist die Wortformulierung eines Ereignisses gesucht.
Ereignisraum
Die Menge aller Ereignisse bildet den Ereignisraum des Zufallsexperiments. Er ist die Menge aller möglichen Teilmengen des Ergebnisraums . Der Ereignisraum ist also nichts anderes als die Potenzmenge der Ergebnismenge und wird daher oft mit bezeichnet.
Wenn die Mächtigkeit ist, so ist die Mächtigkeit der Potenzmenge .
Mit anderen Worten: Wenn der Ergebnisraum aus Elementen besteht, so gibt es verschiedene Ereignisse.
Beispiel
In einer Urne befinden sich eine rote, eine gelbe und eine blaue Kugel. Man zieht eine Kugel aus der Urne. Der Ergebnisraum ist dann gegeben durch: . enthält 3 Elemente, also
Die Menge aller Ereignisse ist dann:
Beispielweise das Ereignis beschreibt "Die Farbe der Kugel ist entweder gelb oder blau".
Es gibt drei mögliche Farben für die gezogene Kugel. Der Ereignisraum enthält also Elemente.
Spezielle Ereignisse
Zu jedem Zufallsexperiment gibt es stets mindestens zwei Ereignisse:
die leere Menge (diese ist die Menge, die kein Element enthält),
und die gesamte Menge (also das Ereignis, das alle Elemente des Ergebnisraums enthält).
Das Ereignis nennt man das unmögliche Ereignis, denn es tritt niemals ein (da dieses Ereignis kein Element enthält, und das Ergebnis eines Zufallsexperiments immer ein Element der Ergebnismenge sein muss).
Das Ereignis nennt man das sichere Ereignis, denn es tritt immer ("mit Sicherheit") ein.
Ereignisse, die nur ein einziges Element enthalten (im obigen Beispiel also die Ereignisse ), nennt man Elementarereignisse
Bildung weiterer Ereignisse aus gegebenen Ereignissen
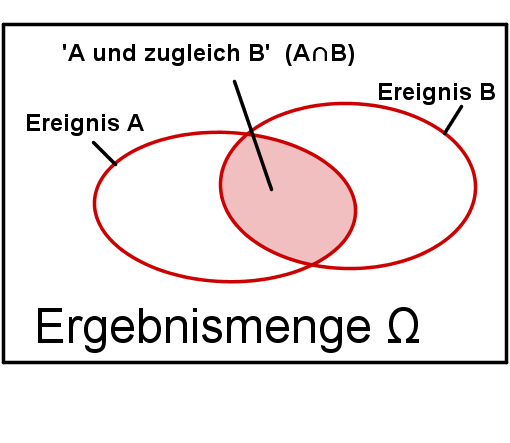
"A und B" (= "A und zugleich B" tritt ein)
Bildet man die Schnittmenge der beiden Ereignisse A und B, also das Ereignis , so erhält man dasjenige Ereignis, das genau dann eintritt, wenn sowohl A als auch B eintreten.
Sonderfall: Unvereinbare Ereignisse
Zwei Ereignisse heißen unvereinbar (disjunkt), wenn ist. Es gibt dann kein Element, dass sowohl in also auch in vorkommt.
Bleiben wir am Beispiel vom Werfen eines Würfels. Wenn beide Ereignisse
: "Die Augenzahl ist gerade", und : "Die Augenzahl ist größer als 3"
eintreten, muss die gewürfelte Augenzahl gerade und gleichzeitig größer als 3 sein. Die einzigen beiden Zahlen, die diese Bedingungen erfüllen sind 4 und 6.
Aus den Mengenschreibweisen und können wir die Schnittmenge ablesen. Die einzigen Elemente, die in beiden Mengen vorkommen sind (wieder) 4 und 6, also
Das Ereignis
: "Die Augenzahl ist ungerade",
ist mit dem Ereignis unvereinbar. Keine Zahl kann gleichzeitig gerade und ungerade sein. Die Mengenschreibweise von ist: . Wir können auch hier sehen, dass und kein gemeinsames Element enthalten und somit
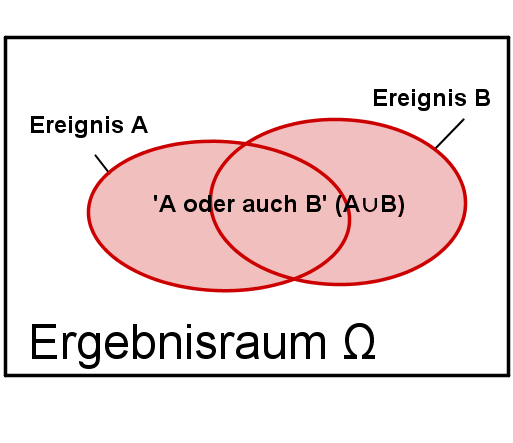
"A oder B" (= "A oder auch B" treten ein)
Bildet man die Vereinigungsmenge der beiden Ereignisse A und B, also das Ereignis , so erhält man das Ereignis, das genau dann eintritt, wenn A oder B (oder beide) eintreten.
(Das "oder" ist also nicht als "entweder - oder" zu verstehen.)
Man bezeichnet dieses Ereignis daher auch als das Ereignis "A oder B" (genauer oder besser: "A oder auch B").
Bleiben wir bei unseren bekannten Ereignissen und so ist das Ereignis A oder B: "Die Augenzahl ist gerade oder größer als 3". In Mengenschreibweise ist dieses Ereignis
"Nicht A" (= Gegenereignis zu A)
Das Gegenereignis von A besteht aus all den Elementen des Ergebnisraumes , die nicht in A sind. Dieses Gegenereignis wird oft mit (gelesen "nicht A") bezeichnet.
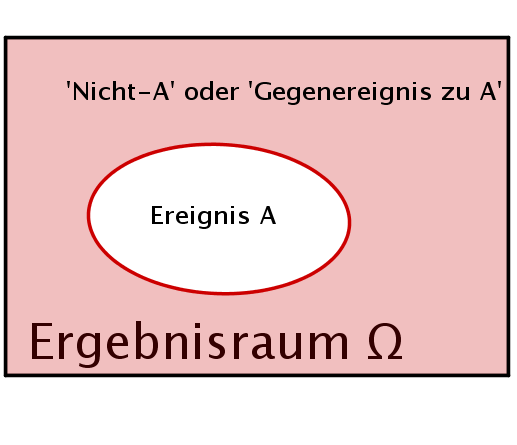
Bei unserem Würfelwurf wäre "Die Augenzahl ist nicht gerade" und damit ().
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Thema Ereignisse
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
