Das Gegenereignis zu einem Ereignis enthält alle Versuchsausgänge, die in nicht enthalten sind.
Beim Werfen eines Würfels wäre das Gegenereignis zu (Augenzahl höchstens ).

Darstellung der Mengen und Gegenereignis beim Werfen eines Würfels.
Das Gegenereignis allgemein
In unserem Beispiel war das Gegenereignis zu . Beide zusammen bilden den Ergebnisraum:
Allgemein ist das Gegenereignis immer die Teilmenge von , die keine Elemente mit gemeinsam hat. Damit bilden und zusammen immer :
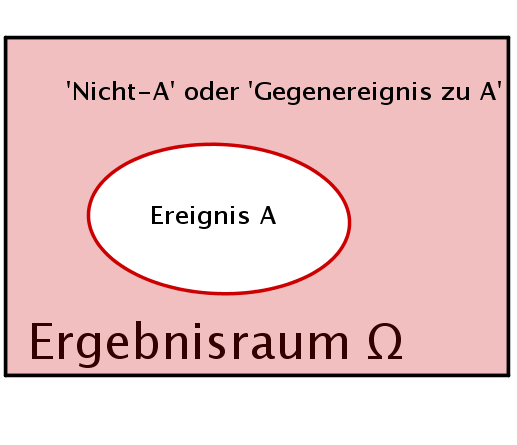
Darstellung der Mengen und Gegenereignis , die gemeinsam bilden.
Die Wahrscheinlichkeit eines Gegenereignisses (Gegenwahrscheinlichkeit) berechnet man, indem man die Wahrscheinlichkeit eines Ereignisses von der Gesamtwahrscheinlichkeit (meist 1) abzieht. In einigen Fällen kann man sich so komplizierte Rechnungen sehr einfach machen.
Beispiele zum Rechnen mit dem Gegenereignis
Beispiel 1
Zufallsexperiment: Ein Würfel wird einmal geworfen.
Ergebnisraum
Ereignis | Der Würfel zeigt die Zahlen 1, 2, 3 oder 4, also |
|---|---|
Wahrscheinlichkeit von | |
Gegenereignis | Der Würfel zeigt die Zahlen 5 oder 6, also |
Gegenwahrscheinlichkeit von |

Darstellung der Mengen und Gegenereignis , die gemeinsam bilden.
Beispiel 2
Zufallsexperiment: Ein Würfel wird zweimal geworfen. Man betrachtet die Summe der Augenzahlen der beiden Würfel.
Ergebnisraum
Ereignis | Die Augensumme beträgt , also |
|---|---|
Wahrscheinlichkeit von | |
Gegenereignis | Die Würfelsumme ist nicht , also |
Gegenwahrscheinlichkeit von |
Das Experiment ist kein Laplace-Experiment. Die Würfelsumme ergibt sich aus 36 verschiedenen Würfelkombinationen, wobei beispielsweise nur eine Kombination die Würfelsumme 2 ergibt und es 3 Kombinationen gibt, die die Würfelsumme 10 bilden.

Darstellung der Mengen und Gegenereignis , die gemeinsam bilden.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
