Vereinigungsmenge

Wenn $A$ und $B$ Mengen sind, dann ist die Vereinigungsmenge von $A$ und $B$ die Menge, die alle Elemente aus $A$ und alle Elemente aus $B$ enthält.

Man schreibt $A\cup B\;$ für die Vereinigungsmenge der Mengen $A$ und $B$ .

Der " $\cup$ " Operator gehört zu den Operatoren, die zwei oder mehrere Mengen verknüpft.

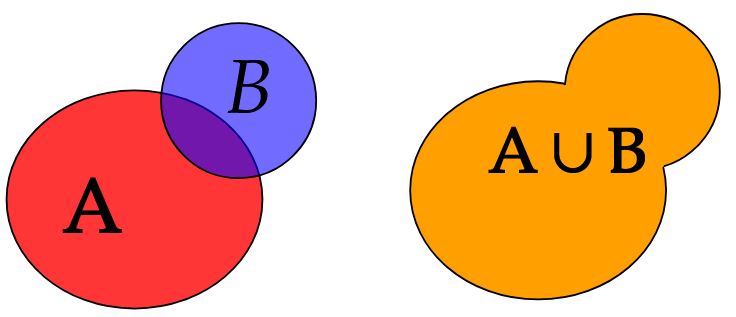
Beispiel zur Vereinigungsmenge

Gegeben sind die Mengen $A$ und $B$ mit

$A=\left\{2{,}3,\mathrm c,\mathrm d\right\}$

$B=\left\{3{,}7,\mathrm a,\mathrm b;\mathrm c\right\}$

Dann ist $A\cup B=\left\{2{,}3,7,\mathrm a,\mathrm b,\mathrm c,\mathrm d\right\}$ die Vereinigungsmenge von $A$ und $B$ .

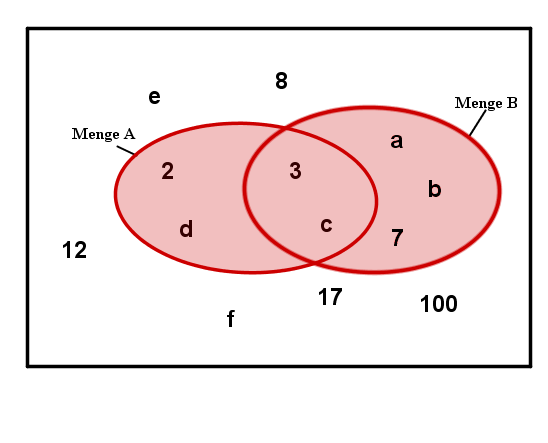
Die nebenstehende Abbildung veranschaulicht das Beispiel mithilfe eines Venn-Diagramms.

Rechenregeln

Der " $\cup$ " Operator ist:

Kommutativ: $A\cup B =B\cup A$
Assoziativ: $(A\cup B) \cup C=A\cup (B\cup C)$

verknüpft mit der Schnittmenge auch

Distributiv: $(A\cup B) \cap C=(A\cap C) \cup(B\cap C)$
- und $(A\cap B) \cup C=(A\cup C) \cap(B\cup C)$

und mit dem „ $\setminus$ “ Operator gilt auch die „De Morgan′sche Regel“:

\displaystyle A\setminus(B\cup C)=(A\setminus B)\cup(A\setminus C)

Übungsaufgaben

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Thema Ereignisse

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Schnittmenge

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?