Teilmenge einer Menge

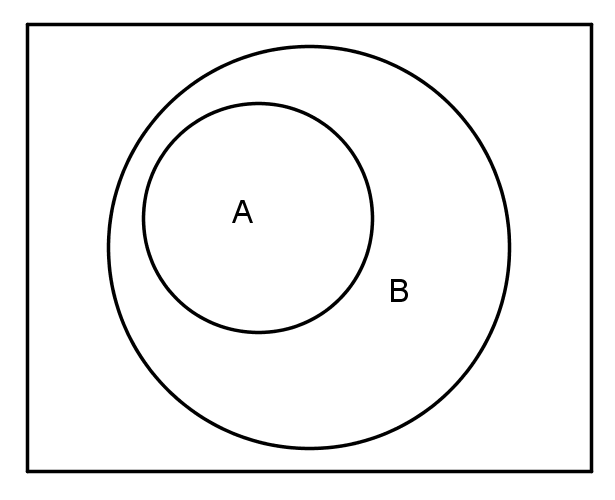
Eine Teilmenge heißt eigentliche oder echte Teilmenge, falls $A$ und $B$ nicht die gleichen Mengen sind, falls also $A \subseteq B$ und $A\ne B$ ist. Hierfür ist die Schreibweise $A\subsetneq B$ üblich.

Anmerkungen

• $\varnothing\subseteq A\subset G$

  Die leere Menge ist Teilmenge jeder Menge und jede Menge muss Teilmenge der Grundmenge sein.

• $A\subseteq A$

  Jede Menge ist (unechte) Teilmenge von sich selbst.

• Wenn $A\subseteq B$ und $B\subseteq A$, dann sind $A$ und $B$ die gleiche Menge: $A=B$

• Wenn $A\subseteq B$ und $B\subseteq C$, dann ist auch $A\subseteq C$.

• $A\subseteq\left(A\cup B\right)$

  Jede Menge ist Teilmenge der Vereinigung von sich mit einer anderen Menge

• $\left( A\cap B\right)\subseteq A$

  Der Schnitt einer Menge mit einer anderen Menge ist immer Teilmenge der ursprünglichen Menge

• Für die Mächtigkeit einer Teilmenge $A\subseteq B$ gilt: $\left| A\right|\leq\left| B\right|$

Potenzmenge

Als Potenzmenge  $\mathcal P\left( A\right)$ bezeichnet man die Menge aller Teilmengen von $A$.

Bei $A=\left(1,\;2,\;3\right)$  ist  $\mathcal P(A)\;=\;\left(\varnothing,\left\{1\right\},\left\{2\right\},\left\{3\right\},\left\{1{,}2\right\},\left\{1{,}3\right\},\left\{2{,}3\right\},\left\{1{,}2,3\right\}\right)$ .

Hierbei ist zu beachten, dass diese Menge selbst Mengen enthält.

$\left\{\left\{1\right\}\right\}$ und $\left\{1\right\}$ sind nicht das gleiche.

Die Mächtigkeit der Potenzmenge $\left|\mathcal P(A)\right|$ , kann berechnet werden durch  $\left| \mathcal P( A)\right|=2^{\left| A\right|}\;$ .

In jeder Teilmenge hat jedes Element 2 Möglichkeiten, es ist enthalten, oder eben nicht.

Im Beispiel ist also $\left|\mathcal P( A)\right|=2^{\left| A\right|}\;=2^3=8$.