Abgebildet ist ein Viertelzylinder (siehe Skizze). Berechne seinen Oberflächeninhalt.
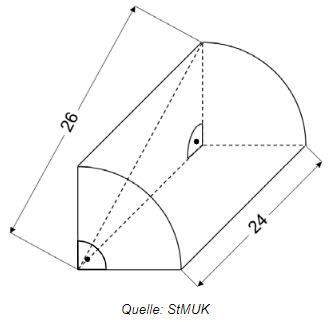
Viertelzylinder
Hinweise: Skizze nicht maßstabsgetreu. Maße in cm
Abgebildet ist ein Viertelzylinder (siehe Skizze). Berechne seinen Oberflächeninhalt.

Viertelzylinder
Hinweise: Skizze nicht maßstabsgetreu. Maße in cm