Teil 2 Analysis 2 - lernen mit Serlo!

Für den Hintergrund einer Modelleisenbahn soll mithilfe eines 3D-Druckers eine Berglandschaft gedruckt werden. Der Graph $G_{k}$ der Funktion $k$ mit der Gleichung $k (x) = a (x^{2} + 1) \cdot e^{- x}$ , $a \in ℝ$ und dem Definitionsbereich $D_{k} = [0; 10]$ beschreibt die obere Kontur der Berglandschaft. Die Variable $x$ gibt den Abstand vom linken Rand der Berglandschaft in cm und der Funktionswert $k (x)$ die Höhe der Konturlinie in cm über dem Boden an.

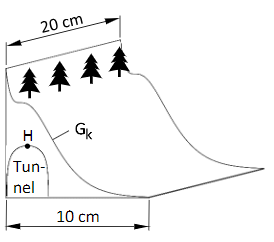
Auf die Mitführung von Einheiten während der Rechnungen kann verzichtet werden. Runden Sie Ihre Ergebnisse gegebenenfalls auf zwei Nachkommastellen.

Die Funktion $k$ ist im gesamten Definitionsbereich streng monoton abnehmend. Bestimmen Sie den Wert des Parameters $a$ , wenn die Berglandschaft an ihrem höchsten Punkt $9$ cm hoch sein soll.
Für die folgenden Teilaufgaben gilt: $k (x) = 9 \cdot (x^{2} + 1) \cdot e^{- x}$
An der Berglandschaft sollen Bäumchen befestigt werden. Damit diese aufrecht stehen, müssen sie an einer Stelle mit waagrechter Tangente angebracht werden. Berechnen Sie dazu die Koordinaten des Punktes auf der Konturlinie, der diese Bedingung erfüllt
Zeigen Sie, dass die Funktion $K$ mit $K (x) = - 9 \cdot (x^{2} + 2 x + 3) \cdot e^{- x}$ mit $D_{k} = [0; 10]$ eine Stammfunktion von $k$ ist.
Bestimmen Sie den Wert des Integrals $I = 20 \cdot \int_{0}^{10} k (x) d$ x
und interpretieren Sie Ihr Ergebnis im Sachzusammenhang.
[ Teilergebnis: $I \approx 539,00$ ]
Zur Herstellung der Berglandschaft wird Kunstharz zu einem Preis von $59,90$ € für $1000 c m^{3}$ benötigt. Ermitteln Sie den Materialpreis für eine Berglandschaft gleicher Form, die nicht $20 c m$ sondern ein Meter lang ist. Verluste an Kunstharz durch den Herstellungsprozess sollen dabei nicht berücksichtigt werden.
Nun wird zusätzlich die Funktion $h$ mit $h (x) = l n (- x^{2} + 4 x) + 2$ in dem maximalen Definitionsbereich $D_{h} =] 0; 4 [$ betrachtet. Der Teil des Graphen $G_{h}$ der Funktion $h$ , der über der x-Achse liegt, beschreibt die Begrenzungslinie eines Tunnels (siehe Aufgabenstellung), der nach der Herstellung durch den 3D-Drucker in die Berglandschaft gefräst werden soll.
1) Für die Kalibrierung der Fräse werden die Schnittpunkte von $G_{h}$ mit der x-Achse benötigt. Ermitteln Sie die x-Koordinaten dieser Schnittpunkte.
2) Der Punkt $H$ (siehe Aufgabenstellung) ist der höchste Punkt des Tunnels (Nachweis nicht erforderlich). Berechnen Sie die Koordinaten des Punktes $H .$

Dieses Werk wurde vom Bayerischen Staatsministerium für Unterricht und Kultus zur Verfügung gestellt. → Was bedeutet das?