In einem kartesischen Koordinatensystem des sind die Punkte , , und ) Eckpunkte der Pyramide mit der dreieckigen Grundfläche .
Zeichnen Sie die Pyramide in das unten abgebildete Koordinatensystem ein.
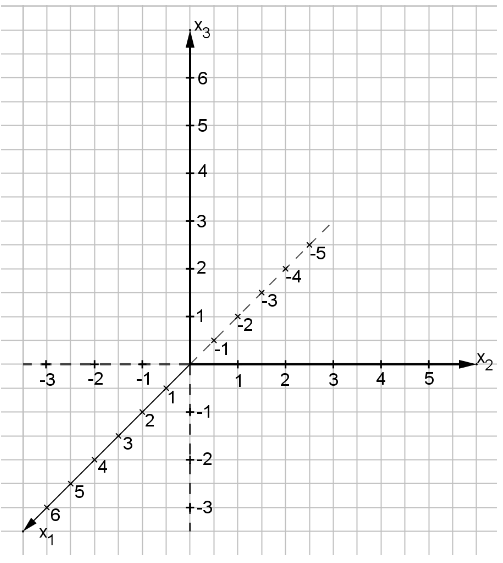
Die Gerade steht senkrecht auf der Grundfläche der Pyramide, verläuft durch den Punkt und schneidet die Grundfläche im Punkt Geben Sie die Gleichung der Geraden sowie die Koordinaten des Schnittpunktes an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

