Die Abbildung zeigt modellhaft einen Teil eines Klettergerüsts auf einem Spielplatz, das in einem kartesischen Koordinatensystem des beschrieben wird. Die Fußpunkte der Stützen des Klettergerüsts liegen in der -Ebene und dazu parallel die rechteckige Plattform . Über ein dreieckiges Netz, das an den Punkten , und fixiert ist, können die Kinder auf die Plattform klettern. Folgende Punkte sind gegeben: , und . Die Koordinaten der Punkte sind Längenangaben in der Einheit Meter. Auf die Mitführung der Einheiten kann verzichtet werden. Runden Sie Ihre Ergebnisse sinnvoll.
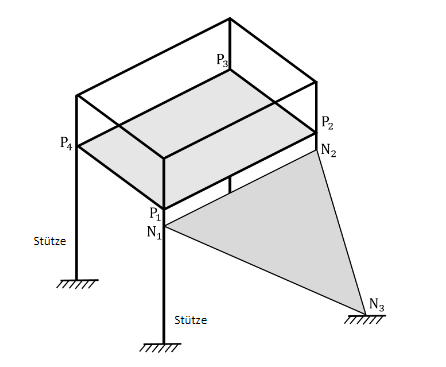
Geben Sie die Koordinaten des Punktes an. (2 BE)
Das Netz ist in den Punkten und befestigt, die jeweils senkrecht unter den Punkten und liegen. Berechnen Sie die Maßzahl des Flächeninhalts des Netzes. (4 BE)
Bestimmen Sie den Winkel zwischen dem Netz und der -Ebene. (3 BE)
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
