Teil 2 Lineare Algebra und analytische Geometrie I

🎓 Prüfungsbereich für Bayern

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

Die Aufgaben zum Ausdrucken als PDF findest du hier.

Bei der Bearbeitung der Aufgaben dürfen Hilfsmittel verwendet werden.

1
In einem kartesischen Koordinatensystem des $ℝ^{3}$ sind der Punkt $A (2 | – 1 | – 4)$ sowie die Geraden
g: $\vec{x} = (\begin{array}{c} 4 \\ 0 \\ - 3 \end{array}) + α (\begin{array}{c} 2 \\ 1 \\ 2 \end{array})$ und $h_{k}$ : $\vec{x} = (\begin{array}{c} 4,5 \\ 4 \\ - 1 \end{array}) + μ (\begin{array}{c} k \\ - 2 \\ 2 \end{array})$ mit $α, μ, k \in ℝ$ gegeben.
Es gilt $A \notin g$ . Somit legen der Punkt $A$ und die Gerade $g$ eine Ebene $E$ fest.
1. Ermitteln Sie je eine Gleichung der Ebene $E$ in Parameter-und Koordinatenform.
  [ Mögliches Teilergebnis: E: $x_{1} - 2 x_{2} - 4 = 0]$
2. Bestimmen Sie den Wert von $k$ so, dass sich die Geraden $g$ und $h_{k}$ in einem Punkt $S$ schneiden und berechnen Sie die Koordinaten dieses Schnittpunktes $S$ .
3. Für $k = - 4$ ergibt sich die Gerade $h_{4}$ : $\vec{x} = (\begin{array}{c} 4,5 \\ 4 \\ - 1 \end{array}) + μ (\begin{array}{c} - 4 \\ - 2 \\ 2 \end{array})$
  Zeigen Sie, dass die Gerade $h_{- 4}$ echt parallel zur Ebene $E$ verläuft. Fertigen Sie ohne Verwendung eines Koordinatensystems eine aussagekräftige Skizze an, aus der die gegenseitige Lage von $E$ sowie der beiden Geraden $h_{4}$ und $g$ klar hervorgeht. Formulieren Sie die Lagebeziehung zwischen $h_{4}$ und $g$ zusätzlich in Worten.
2
Die Abbildung zeigt modellhaft einen Teil eines Klettergerüsts auf einem Spielplatz, das in einem kartesischen Koordinatensystem des $ℝ^{3}$ beschrieben wird. Die Fußpunkte der Stützen des Klettergerüsts liegen in der $x_{1} x_{2}$ -Ebene und dazu parallel die rechteckige Plattform $P_{1} P_{2} P_{3} P_{4}$ . Über ein dreieckiges Netz, das an den Punkten $N_{1}$ , $N_{2}$ und $N_{3}$ fixiert ist, können die Kinder auf die Plattform $P_{1} P_{2} P_{3} P_{4}$ klettern. Folgende Punkte sind gegeben: $P_{1} (1,8 | 1,2 | 1,5)$ , $P_{2} (0 | 1,2 | 1,5$ ), $P_{3} (0 | 0 | 1,5)$ und $N_{3} (0,9 | 3,6 | 0)$ . Die Koordinaten der Punkte sind Längenangaben in der Einheit Meter.
Auf die Mitführung der Einheiten kann verzichtet werden. Runden Sie Ihre Ergebnisse sinnvoll.
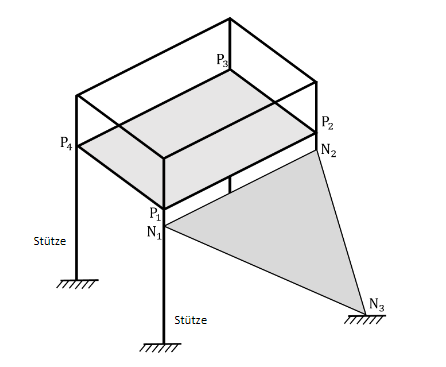
1. Geben Sie die Koordinaten des Punktes $P_{4}$ an.
2. Das Netz ist in den Punkten $N_{1}$ und $N_{2}$ befestigt, die jeweils $10 c m$ senkrecht unter den Punkten $P_{1}$ und $P_{2}$ liegen. Berechnen Sie die Maßzahl des Flächeninhalts des Netzes.
3. Bestimmen Sie den Winkel zwischen dem Netz und der $x_{1} x_{2}$ -Ebene.

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?