Eine Skulptur aus Leichtmetall in einer Kunsthalle hat die Form eines nicht symmetrischen Trapezes , aus dem ein Dreieck ausgeschnitten wurde. Das Trapez wird modellhaft in einem kartesischen Koordinatensystem des betrachtet. Der Hallenboden liegt in der -Koordinatenebene und der Punkt im Koordinatenursprung. Die Punkte , , und bilden die Eckpunkte des Trapezes. Die Koordinaten der Punkte sind Längenangaben in der Einheit Dezimeter. Auf die Mitführung von Einheiten während der Rechnungen kann verzichtet werden.
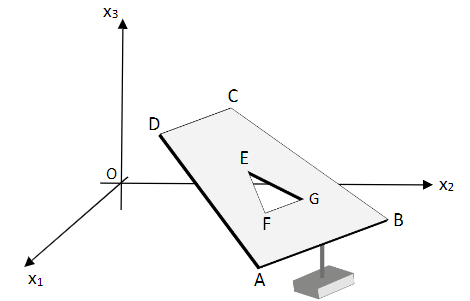
Die Punkte und legen die Ebene fest. Ermitteln Sie jeweils eine Gleichung von in Parameter- und Koordinatenform.
[ Mögliches Teilergebnis: ]
Berechnen Sie den Neigungswinkel der Trapezfläche gegenüber dem Hallenboden. Runden Sie Ihr Ergebnis auf zwei Nachkommastellen.
Erläutern Sie, wie Sie den Inhalt der Trapezfläche berechnen können, ohne diese Rechnung konkret durchzuführen. Hinweis: Die ausgeschnittene Dreiecksfläche ist bei der Erläuterung nicht zu berücksichtigen.
Der Punkt ist der Schnittpunkt der beiden Diagonalen und (siehe Skizze). Bestimmen Sie die Koordinaten des Punktes .
[Mögliches Ergebnis: ]
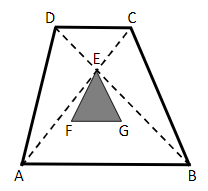
Für den Punkt des Dreiecks gilt: . Berechnen Sie die Maßzahl der Länge der Dreiecksseite und die Koordinaten des Punktes , wenn die Dreiecksseite parallel zu ist und gilt.
