Auf der Außenwand eines neuen Hallenbades soll dessen Logo, eine Welle, abgebildet werden. Der Architekt möchte ein großes Fenster in Form eines rechtwinkligen Dreiecks (siehe Skizze ) innerhalb der Welle anbringen.
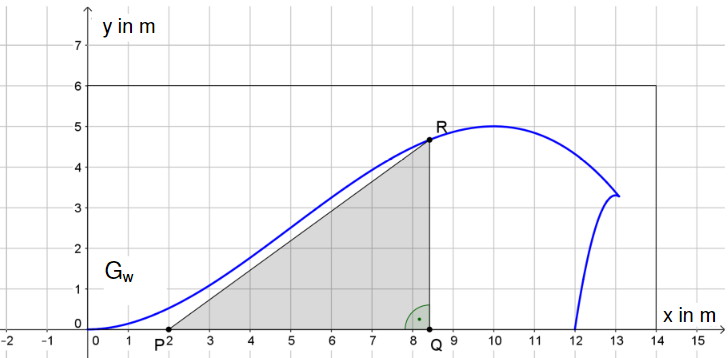
Das Fenster soll am Punkt beginnen. Seine Breite | | soll mindestens und höchstens betragen. Der Punkt soll auf der oberen Begrenzungslinie (Graph ) der Welle liegen, welche durch die Funktion beschrieben wird. Bei Berechnungen kann auf Einheiten verzichtet werden.
Zeigen Sie, dass die Maßzahl der Fläche des Fensters abhängig von der -Koordinate des Punktes durch die Funktionsgleichung beschrieben wird, und geben Sie für die Funktion einen Definitionsbereich an, der den Vorgaben von Aufgabe 4 entspricht.
Der Architekt möchte das Hallenbad möglichst hell gestalten. Aus diesem Grund soll die Fläche des Fensters möglichst groß sein. Bestimmen Sie die -Koordinate des Punktes , für welche die Maßzahl der Fläche maximal wird. Berechnen Sie für diesen Fall Breite, Höhe und Fläche des Fensters. Ermitteln Sie den prozentualen Anteil der Fensterfläche an der Logofläche, wenn diese beträgt. Runden Sie Ihre Ergebnisse auf zwei Nachkommastellen.
