Aufgabe 4
Die Aufgabe 4 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist .
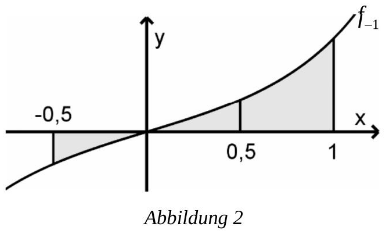
Begründen Sie unter Verwendung der Abbildung 2, dass gilt. (2 P)
Die Aufgabe 4 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist .
Begründen Sie unter Verwendung der Abbildung 2, dass gilt. (2 P)
