B5

🎓 Prüfungsbereich für Nordrhein-Westfalen

Weitere Bundesländer & Aufgaben:
Mathe- Prüfungen Startseite

Austausch & Hilfe:
Prüfungen-Discord

1
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 1
Gegeben ist die Schar der in $ℝ$ definierten Funktionen $f_{a}$ mit der Gleichung
$f_{a} (x) = x \cdot e^{- \frac{1}{2} \cdot a \cdot x^{2} + \frac{1}{2}} mit a \in ℝ$ .
Die zugehörigen Graphen sind symmetrisch bezüglich des Koordinatenursprungs. Zunächst werden einzelne Funktionen der Schar betrachtet.
Der Graph von $f_{1}$ hat den Hochpunkt $H_{1} (1 | 1)$ .
1. Weisen Sie nach, dass $f_{1}$ genau eine Nullstelle hat, und geben Sie den Grenzwert von $f_{1}$ für $x \to \infty$ an. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Nullstelle
  Weise nach, dass $f_{1}$ genau eine Nullstelle hat
  Gegeben ist $f_{a} (x) = x \cdot e^{- \frac{1}{2} \cdot a \cdot x^{2} + \frac{1}{2}}$ .
  Dann ist $f_{1} (x) = x \cdot e^{- \frac{1}{2} \cdot 1 \cdot x^{2} + \frac{1}{2}}$
  Ein Produkt ist null, wenn einer der Faktoren null ist (Satz vom Nullprodukt).
  $f (x) = 0 \Rightarrow 0 = x \cdot \underset{\neq 0}{\underset{⏟}{e^{- \frac{1}{2} x^{2} + \frac{1}{2}}}} \Rightarrow x = 0$
  Somit hat $f_{1}$ nur eine Nullstelle.
  Gib den Grenzwert von $f_{1}$ für $x \to \infty$ an
  $\lim_{x \to \infty} (\underset{\to \infty}{\underset{⏟}{x}} \cdot \underset{\to 0^{+}}{\underset{⏟}{e^{- \frac{1}{2} x^{2} + \frac{1}{2}}}}) = 0^{+}$
  Der Exponent der $e$ -Funktion hat den Grenzwert $- \infty$ . Die $e$ -Funktion geht dort stärker gegen $0$ , als $x \to \infty$ geht.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Ein Produkt ist null, wenn einer der Faktoren null ist (Satz vom Nullprodukt).
  Löse $f (x) = 0$ .
  Teil 2
  Beachte, wenn $x$ gegen unendlich geht, geht die Funktion $e^{- \frac{1}{2} x^{2} + \frac{1}{2}}$ stärker gegen null.
  Welchen Grenzwert erhält man dann?
2. Abbildung 1 zeigt den Graphen von $f_{1}$ ohne das zugrunde liegende Koordinatensystem.
  Zeichnen Sie die Koordinatenachsen mit der passenden Skalierung in die Abbildung ein. (2 P)
  Abbildung 1
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Das Koordinatensystem
  Zeichne die Koordinatenachsen mit der passenden Skalierung in die Abbildung ein
  Der Graph von $f_{1}$ ist punktsymmetrisch zum Koordinatenursprung und es gilt nach a) $\lim_{x \to \infty} f_{1} (x) = 0$ . Damit sind die beiden Achsen festgelegt.
  Weiterhin sind $f_{1} (1) = 1$ und $f_{1} (- 1) = - 1$ . Damit kann eine Skalierung vorgenommen werden.
  Abbildung 1
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Der Graph von $f_{1}$ ist punktsymmetrisch zum Koordinatenursprung und es gilt nach a) $\lim_{x \to \infty} f_{1} (x) = 0$ . Damit sind die beiden Achsen festgelegt.
  Weiterhin sind $f_{1} (1) = 1$ und $f_{1} (- 1) = - 1$ . Damit kann eine Skalierung vorgenommen werden.
3. Interpretieren Sie den folgenden Sachverhalt geometrisch:
  Für jede Stammfunktion $F_{1}$ von $f_{1}$ und für jede reelle Zahl $u > 2022$ gilt:
  $F_{1} (u) - F_{1} (0) \approx \int_{0}^{2022} f_{1} (x) d x$ . (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
  Interpretiere den Sachverhalt geometrisch
  Das Integral $\int_{0}^{2022} f (x) d x$ berechnet den Flächeninhalt zwischen $f (x)$ und der $x$ -Achse im Bereich von $0$ bis $2022$ (siehe Abbildung $1$ mit Koordinatenachsen).
  Entsprechend wird mit $F_{1} (u) - F_{1} (0)$ ebenfalls der Flächeninhalt zwischen $f (x)$ und der $x$ -Achse im Bereich von $0$ bis $u$ berechnet. Ist $u > 2022$ , dann unterscheiden sich die beiden Flächeninhalte nicht mehr wesentlich voneinander. Sie sind ungefähr gleich groß.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Was berechnet das Integral $\int_{0}^{2022} f (x) d x$ ?
  Was wird durch $F_{1} (u) - F_{1} (0)$ berechnet?
  Welche Aussage über die beiden Flächeninhalte wird getroffen, wenn $u > 2022$ ist?
2
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 2
Die Aufgabe 2 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist $f_{a} (x) = x \cdot e^{- \frac{1}{2} \cdot a \cdot x^{2} + \frac{1}{2}} mit a \in ℝ$ .
Der Graph von $f_{0}$ ist eine Gerade.
1. Geben Sie die Steigung dieser Geraden und die Koordinaten ihres Schnittpunktes mit der $y$ -Achse an. (2 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradensteigung
  Gib die Steigung dieser Geraden an
  Es ist $f_{0} (x) = x \cdot e^{- \frac{1}{2} \cdot 0 \cdot x^{2} + \frac{1}{2}} = x \cdot e^{\frac{1}{2}} = e^{\frac{1}{2}} \cdot x$ .
  Die Steigung der Geraden ist $e^{\frac{1}{2}}$ .
  Gib die Koordinaten ihres Schnittpunktes mit der $y$ -Achse an
  Es ist $f_{0} (x) = e^{\frac{1}{2}} \cdot x$ .
  Den Schnittpunkt mit der y-Achse erhält man für $x = 0 \Rightarrow f_{0} (0) = e^{\frac{1}{2}} \cdot 0 = 0$ .
  $S (0 | 0)$ ist der Schnittpunkt mit der $y$ -Achse.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Teil 1
  Setze $a = 0$ in $f_{a} (x)$ ein und fasse zusammen.
  Teil 2
  Den Schnittpunkt mit der y-Achse erhält man für $x = 0$ .
  Setze in $f_{0} (x)$ ein.
3
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 3
Die Aufgabe 3 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist $f_{a} (x) = x \cdot e^{- \frac{1}{2} \cdot a \cdot x^{2} + \frac{1}{2}} mit a \in ℝ$ .
Für einen Wert von $a$ liegt der Punkt $P (1 | e)$ auf dem Graphen von $f_{a}$ .
Bestimmen Sie diesen Wert von $a$ und die Steigung der Tangente an den Graphen von $f_{a}$ im Punkt $P$ . (3 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Tangente an Graph
Bestimme diesen Wert von $a$
Der Punkt $P (1 | e)$ liegt auf dem Graphen von $f_{a}$ .
$f_{a} (1) = 1 \cdot e^{- \frac{1}{2} \cdot a \cdot 1^{2} + \frac{1}{2}} = e^{- \frac{1}{2} \cdot a + \frac{1}{2}}$
$\Rightarrow e = e^{- \frac{1}{2} \cdot a + \frac{1}{2}} \Rightarrow - \frac{1}{2} \cdot a + \frac{1}{2} = 1 \Rightarrow a = - 1$
Der Wert von $a = - 1$ .
Bestimme die Steigung der Tangente an den Graphen von $f_{a}$ im Punkt $P$
Es ist $f_{- 1} (x) = x \cdot e^{\frac{1}{2} \cdot x^{2} + \frac{1}{2}}$ .
Die 1. Ableitung von $f_{- 1} (x)$ ist:
$f_{- 1}^{'} (x) = (1 + x^{2}) \cdot e^{\frac{1}{2} \cdot x^{2} + \frac{1}{2}} \Rightarrow f_{- 1}^{'} (1) = (1 + 1^{2}) \cdot e^{\frac{1}{2} \cdot 1^{2} + \frac{1}{2}} = 2 \cdot e^{1} = 2 \cdot e = m_{t}$
Die Steigung der Tangente an den Graphen von $f_{a}$ im Punkt $P$ ist $m_{t} = 2 \cdot e$ .
Teil 1
Der Punkt $P (1 | e)$ liegt auf dem Graphen von $f_{a}$ .
Setze die Koordinaten des Punktes in $f_{a} (x)$ ein und löse nach $a$ auf.
Teil 2
Setze $- 1$ in $f_{- 1}^{'} (x)$ ein.
4
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Aufgabe 4
Die Aufgabe 4 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist $f_{a} (x) = x \cdot e^{- \frac{1}{2} \cdot a \cdot x^{2} + \frac{1}{2}} mit a \in ℝ$ .
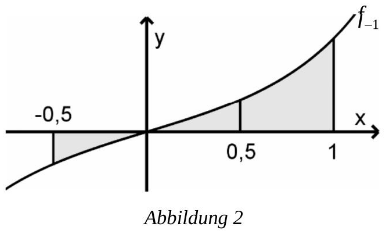
Begründen Sie unter Verwendung der Abbildung 2, dass $\int_{- 0,5}^{1} f_{- 1} (x) d x = \int_{0,5}^{1} f_{- 1} (x) d x$ gilt. (2 P)
Für diese Aufgabe benötigst Du folgendes Grundwissen: Flächenberechnung mit Integralen
Begründe unter Verwendung der Abbildung 2, dass $\int_{- 0,5}^{1} f_{- 1} (x) d x = \int_{0,5}^{1} f_{- 1} (x) d x$ gilt
Da der Graph punktsymmetrisch zum Koordinatenursprung verläuft, ist das Flächenstück zwischen dem Graphen von $f_{1}$ und der x-Achse für das Intervall $[- 0,5; 0]$ genauso groß wie das Flächenstück für das Intervall $[0; 0,5]$ . Da das erste Flächenstück unterhalb und das zweite Flächenstück oberhalb der x-Achse liegt, muss $\int_{- 0,5}^{0,5} f_{- 1} (x) d x = 0$ gelten.
Demnach ist $\int_{- 0,5}^{1} f_{- 1} (x) d x = \underset{= 0}{\underset{⏟}{\int_{- 0,5}^{0,5} f_{- 1} (x) d x}} + \int_{0,5}^{1} f_{- 1} (x) d = \int_{0,5}^{1} f_{- 1} (x) d$
Beachte die beiden Flächen unterhalb und oberhalb der x-Achse. Sie sind gleich groß.
Was bedeutet das für das Integral $\int_{- 0,5}^{0,5} f_{- 1} (x) d x$ ?
5
Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen (Gilt für: Aufgabenstellung)Diese Aufgabe stammt vom Ministerium für Schule und Bildung des Landes Nordrhein-Westfalen --- Die Nutzung könnte vielleicht strengeren Regeln unterliegen als bei unseren anderen Inhalten.
Die Aufgabe 5 ist eine Fortsetzung der Aufgabe 1.
Gegeben ist $f_{a} (x) = x \cdot e^{- \frac{1}{2} \cdot a \cdot x^{2} + \frac{1}{2}} mit a \in ℝ$ .
Nun werden alle Funktionen der gegebenen Schar betrachtet.
1. Die folgenden Aussagen gelten für alle reellen Zahlen $a, a_{1}$ und $a_{2}$ :
  I) $f_{a} (0) = 0$
  II) $f_{a}^{'} (0) = f_{0}^{'} (0)$
  III) $f_{a_{1}} (x) = f_{a_{2}} (x) \Leftrightarrow a_{1} = a_{2} \lor x = 0$
  Geben Sie an, was sich aus diesen Aussagen hinsichtlich des Verlaufs der Graphen der Schar folgern lässt. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Graph einer Funktion
  Gib an, was sich aus diesen Aussagen hinsichtlich des Verlaufs der Graphen der Schar folgern lässt
  I) Alle Graphen der Schar schneiden sich im Koordinatenursprung.
  II) Im Koordinatenursprung haben alle Graphen der Schar die gleiche Steigung.
  III) Keiner der Graphen hat einen weiteren Punkt mit einem anderen Graphen der Schar gemeinsam.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  I) Was gilt für $x = 0$ ?
  II) Was gilt für die Steigung an der Stelle $x = 0$ ?
  III) Gibt es außer dem Koordinatenursprung noch einen weiteren Punkt, den ein Graph der Schar mit einem anderen Graphen der Schar gemeinsam hat?
2. Für alle $a \neq 0$ stimmen die Wendestellen von $f_{a}$ mit den Lösungen der Gleichung $(a \cdot x^{2} - 3) \cdot x = 0$ überein.
  Geben Sie für alle Werte von $a \in ℝ$ die Anzahl der Wendestellen von $f_{a}$ an und begründen Sie Ihre Angabe. (1 P + 4 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Wendepunkte und Terrassenpunkte
  Gib für alle Werte von $a \in ℝ$ die Anzahl der Wendestellen von $f_{a}$ an und begründe Deine Angabe
  Für $a = 0$ gilt: Da der Graph von $f_{0}$ eine Gerade ist, hat $f_{0}$ keine Wendestellen.
  Für $a \neq 0$ gilt: $(a \cdot x^{2} - 3) \cdot x = 0 \Rightarrow x = 0 \lor x^{2} = \frac{3}{a}$
  Ist $a < 0$ , dann hat die Gleichung nur die Lösung $x = 0$ und $f_{a}$ hat nur eine Wendestelle.
  Ist $a > 0$ , dann hat die Gleichung drei Lösungen und $f_{a}$ hat in diesem Fall drei Wendestellen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Für $a = 0$ betrachte die Lösung der Aufgabe 2.
  Für $a \neq 0$ löse die Gleichung $(a \cdot x^{2} - 3) \cdot x = 0$ und unterscheide die Fälle $a < 0$ und $a > 0$ .
3. Alle Extrempunkte der Graphen der Schar liegen auf einer Geraden.
  Begründen Sie, dass es sich dabei um die Gerade mit der Gleichung $y = x$ handelt. (3 P)
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Symmetrie von Graphen
  Begründe, dass es sich dabei um die Gerade mit der Gleichung $y = x$ handelt
  Nach Aufgabe 1 hat der Graph von $f_{1}$ (Abbildung 1) einen Hochpunkt $H P (1 | 1)$ und einen $T P (- 1 | - 1)$ (aufgrund der Symmetrie zum Ursprung).
  Die Gerade muss also durch diese beiden Punkte verlaufen. Dies ist nur für die Gerade mit der Gleichung $y = x$ der Fall.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Nach Aufgabe 1 hat der Graph von $f_{1}$ (Abbildung 1) einen Hochpunkt $H P (1 | 1)$ und einen $T P (- 1 | - 1)$ .
  Welche Gerade verläuft durch diese beiden Punkte?

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

B5

Aufgabe 1

Weise nach, dass f1 genau eine Nullstelle hat

Gib den Grenzwert von f1 für x→∞ an

Hast du eine Frage oder Feedback?

Zeichne die Koordinatenachsen mit der passenden Skalierung in die Abbildung ein

Hast du eine Frage oder Feedback?

Interpretiere den Sachverhalt geometrisch

Hast du eine Frage oder Feedback?

Aufgabe 2

Gib die Steigung dieser Geraden an

Gib die Koordinaten ihres Schnittpunktes mit der y-Achse an

Hast du eine Frage oder Feedback?

Aufgabe 3

Bestimme diesen Wert von a

Bestimme die Steigung der Tangente an den Graphen von fa im Punkt P

Aufgabe 4

Begründe unter Verwendung der Abbildung 2, dass ∫−0,51f−1(x)dx=∫0,51f−1(x)dx gilt

Gib an, was sich aus diesen Aussagen hinsichtlich des Verlaufs der Graphen der Schar folgern lässt

Hast du eine Frage oder Feedback?

Gib für alle Werte von a∈ℝ die Anzahl der Wendestellen von fa an und begründe Deine Angabe

Hast du eine Frage oder Feedback?

Begründe, dass es sich dabei um die Gerade mit der Gleichung y=x handelt

Hast du eine Frage oder Feedback?

Weise nach, dass $f_{1}$ genau eine Nullstelle hat

Gib den Grenzwert von $f_{1}$ für $x \to \infty$ an

Gib die Koordinaten ihres Schnittpunktes mit der $y$ -Achse an

Bestimme diesen Wert von $a$

Bestimme die Steigung der Tangente an den Graphen von $f_{a}$ im Punkt $P$

Begründe unter Verwendung der Abbildung 2, dass $\int_{- 0,5}^{1} f_{- 1} (x) d x = \int_{0,5}^{1} f_{- 1} (x) d x$ gilt

Gib für alle Werte von $a \in ℝ$ die Anzahl der Wendestellen von $f_{a}$ an und begründe Deine Angabe

Begründe, dass es sich dabei um die Gerade mit der Gleichung $y = x$ handelt