Der Graph einer Funktion ist eine Zeichnung in der Ebene, die die Funktion visualisiert (= graphisch darstellt).
Er kann formal als die Menge von Punkten gesehen werden, bei denen
die x-Koordinate aus dem Definitionsbereich der Funktion ist und
die y-Koordinate der Funktionswert der x-Koordinate ist.
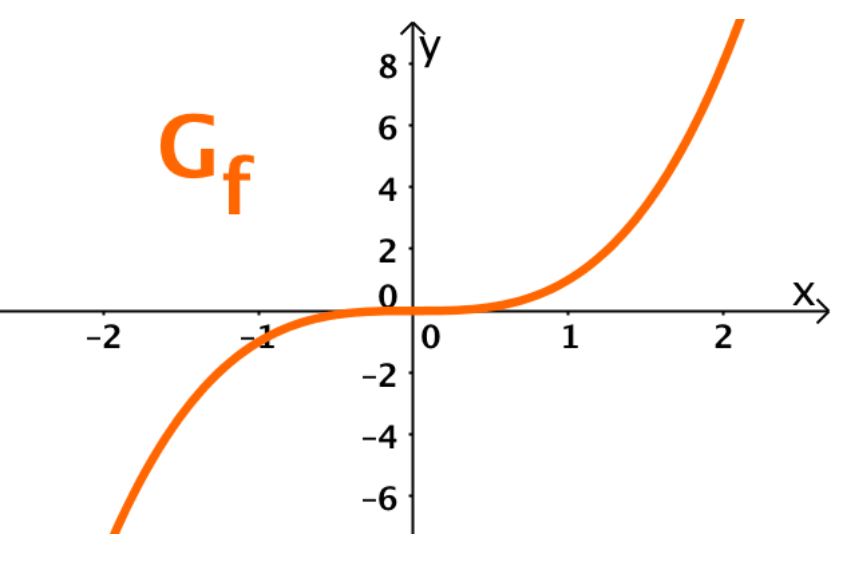
Symbole und Mengenschreibweise
Für den Graphen einer Funktion schreibt man . Als Menge lässt sich wie folgt schreiben:
oder
Graphen mit einer Wertetabelle zeichnen
Die direkteste Methode, einen Graphen zu zeichnen, ist, möglichst viele Punkte des Graphen zu berechnen. Dies geht so:
Eine beliebige Zahl als x-Koordinate wählen
x-Koordinate in den Funktionsterm einsetzen
das Ergebnis f(x) ist dann die y-Koordinate
den Punkt (x, f(x)) in ein Koordinatensystem eintragen
Wenn man einige Punkte des Graphen eingezeichnet hat, kann man den durchgängigen Graphen zeichnen.
Beispiel
Einige Punkte werden hier in eine Wertetabelle eingetragen:
|
| ||||||||
|
|
Nun kann man den Graphen zeichnen, indem man sich an diesen Punkten orientiert. Er sieht wie folgt aus.
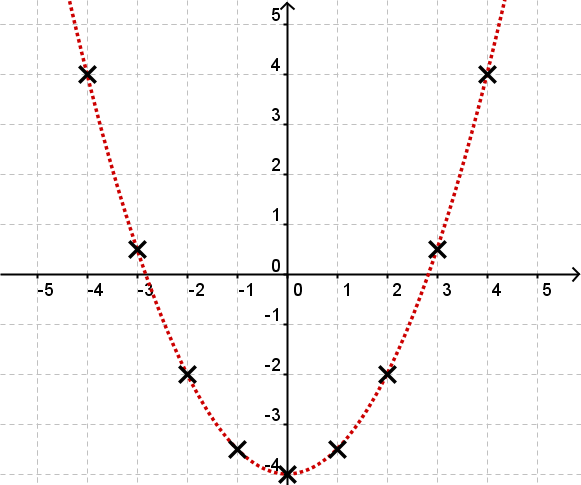
Graphen nach Kurvendiskussion zeichnen
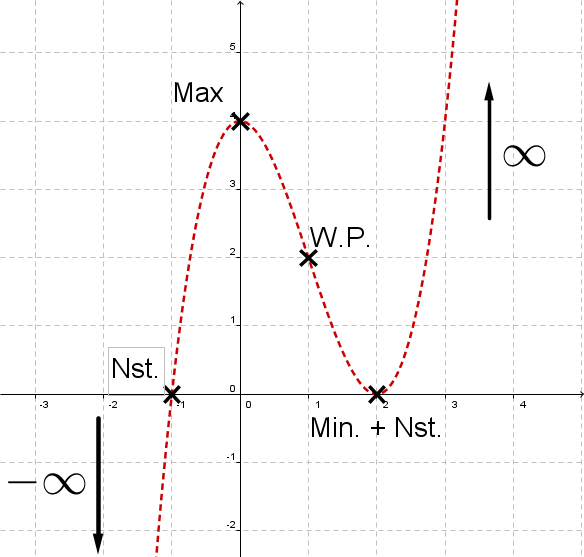
Hat man zuvor schon eine Kurvendiskussion der Funktion ausgeführt, ist es ratsam, die wichtigen Punkte (Minima, Maxima, Nullstellen, Wende- und Terrassenpunkte) des Graphen einzuzeichnen. Mit diesen Punkten als Stützstellen und den Grenzwerten gegen lässt sich der Graph meistens viel leichter nachzeichnen als mit beliebig ausgewählten Punkten.
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu Funktionen und Relationen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
