Ebene

Eine Ebene ist ein Objekt der analytischen Geometrie im dreidimensionalen Raum. Allgemein handelt es sich um ein unbegrenzt ausgedehntes flaches zweidimensionales Objekt.

Darstellungsformen

Ebenen kann man auf verschiedene Weisen darstellen. Hier wird auf die Parameterform, die Koordinatenform, die Normalenform und die Hessesche-Normalenform eingegangen.

Parameterform

Die Parameterform beschreibt die Ebene durch einen Stützvektor und zwei Richtungsvektoren. Jeder Punkt der Ebene wird durch einen Parameter s und t dargestellt.

Parameterform: $E : \vec{x} = \vec{p} + s \cdot \vec{u} + t \cdot {\vec{v}}_{}^{}$

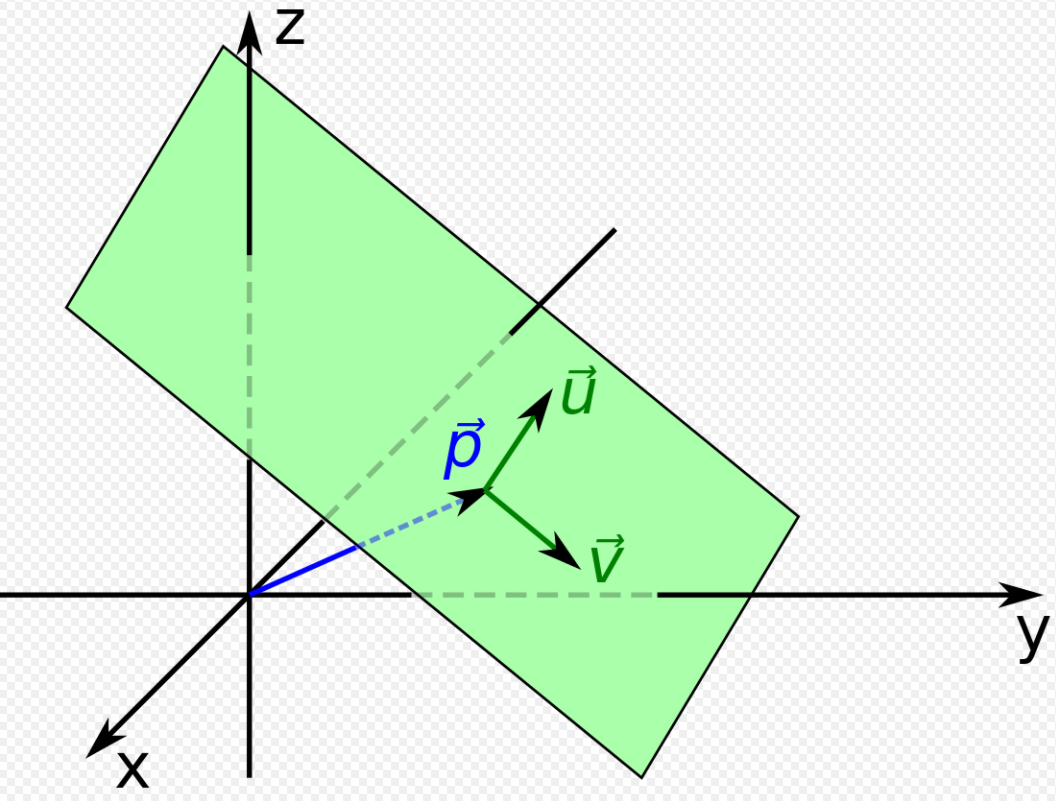
Darstellung der Parameterform einer Ebene — Abb. 1: Ebene aus 2 Richtungsvektoren

Koordinatenform

Die Koordinatenform stellt eine Ebene als lineare Gleichung dar. Jeder Punkt der Ebene erfüllt die lineare Gleichung.

Koordinatenform: $E : a x + b y + c z = d$

Normalenform (auch Normalform)

Um eine Ebene in der Normalenform auszudrücken, benötigt man den Ortsvektor eines Punktes auf der Ebene $\vec{p}$ und einen Normalvektor $\vec{n}$ der Ebene. Jeder Punkt der Ebene erfüllt dann die Gleichung (mit $\circ$ ist hier das Skalarprodukt gemeint).

Normalenform: $E : (\vec{x} - \vec{p}) \circ \vec{n} = 0$

Hessesche Normalenform

Die Hesse-Normalenform (oft mit $HNF (E)$ bezeichnet) ist ein Spezialfall der Normalenform, bei der zusätzlich folgende Bedingungen für $\vec{n}$ erfüllt sind:

$| \vec{n} | = 1$ , d. h. der Normalenvektor ist normiert
$\vec{n} \circ \vec{p} \geq 0$ , d. h. der Normalenvektor zeigt vom Ursprung in Richtung der Ebene

$\vec{n}$ wird dann oft als $\vec{n_{0}}$ gekennzeichnet. $d = \vec{p} \circ {\vec{n}}_{0}$ ist dann der Abstand der Ebene vom Ursprung.

Hessesche Normalenform: $E : (\vec{x} - \vec{p}) \circ {\vec{n}}_{0} = 0$ oder $\vec{x} \circ {\vec{n}}_{0} = d$

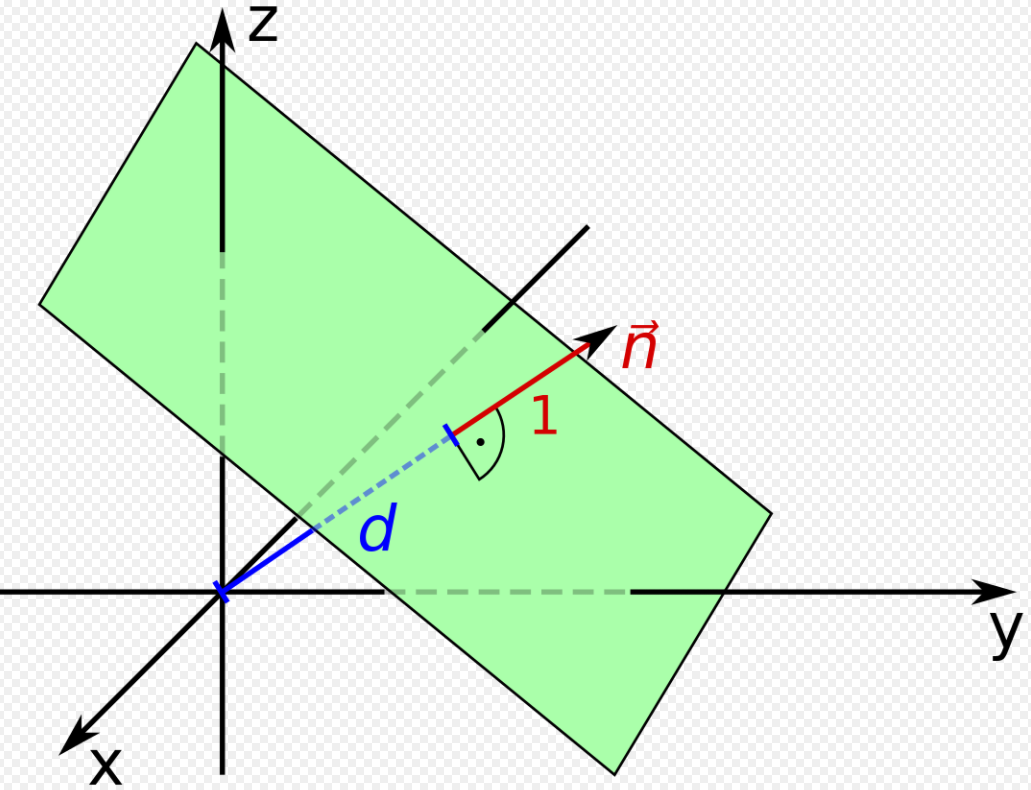
Hessesche Normalenform einer Ebene — Abb. 2: Ebene aus normierten Normalenvektor

Umformungen

In den folgenden Artikeln kannst du nachlesen, wie du die Ebenen von einer Darstellungsform in eine andere umwandeln kannst:

Spurpunkte-Spurgeraden

Als Spurpunkte einer Ebene bezeichnet man die Schnittpunkte mit den Koordinatenachsen, als Spurgeraden die Schnittgeraden mit den Koordinatenebenen. Die Spurgeraden erhält man auch als Verbindungsgeraden der Spurpunkte.

Koordinatenebenen

Die Koordinatenebenen sind die Ebenen, in denen jeweils eine Koordinate gleich null ist. Sie werden je von zwei Standardbasisvektoren aufgespannt:

x-y-Ebene

Parameterform	$\vec{x} = (\begin{array}{c} 0 \\ 0 \\ 0 \end{array}) + s (\begin{array}{c} 1 \\ 0 \\ 0 \end{array}) + t (\begin{array}{c} 0 \\ 1 \\ 0 \end{array}) = (\begin{array}{c} s \\ t \\ 0 \end{array})$
Koordinatenform	$z = 0$
Hessesche Normalenform	$[(\begin{array}{c} x \\ y \\ z \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 0 \end{array})] \circ (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) = 0$

y-z-Ebene

Parameterform	$\vec{x} = (\begin{array}{c} 0 \\ 0 \\ 0 \end{array}) + s (\begin{array}{c} 0 \\ 1 \\ 0 \end{array}) + t (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} 0 \\ s \\ t \end{array})$
Koordinatenform	$x = 0$
Hessesche Normalenform	$[(\begin{array}{c} x \\ y \\ z \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 0 \end{array})] \circ (\begin{array}{c} 1 \\ 0 \\ 0 \end{array}) = 0$

x-z-Ebene

Parameterform	$\vec{x} = (\begin{array}{c} 0 \\ 0 \\ 0 \end{array}) + s (\begin{array}{c} 1 \\ 0 \\ 0 \end{array}) + t (\begin{array}{c} 0 \\ 0 \\ 1 \end{array}) = (\begin{array}{c} s \\ 0 \\ t \end{array})$
Koordinatenform	$y = 0$
Hessesche Normalenform	$[(\begin{array}{c} x \\ y \\ z \end{array}) - (\begin{array}{c} 0 \\ 0 \\ 0 \end{array})] \circ (\begin{array}{c} 0 \\ 1 \\ 0 \end{array}) = 0$

Übungsaufgaben

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Aufstellung von Ebenengleichung

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Kurse

Quellen

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?