Der Definitionsbereich (auch: die Definitionsmenge) gibt an, welche x-Werte in eine Funktion eingesetzt werden dürfen.
Darstellung mit Beispielen
Es gibt verschiedene Möglichkeiten, den Definitionsbereich darzustellen
"Der Definitionsbereich besteht aus , , usw…"
"Der Definitionsbereich sind alle Zahlen von bis "
"Der Definitionsbereich sind alle reellen Zahlen außer "
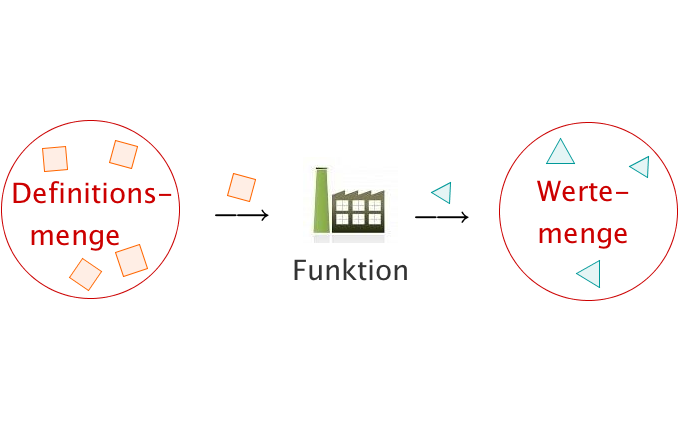
Video zum Definitions- und Wertebereich
Definitionslücken
Um den Definitionsbereich einer Funktion zu bestimmen, muss man sie auf Definitionslücken prüfen.
Definitionslücken sind Werte, die in eine Funktion nicht eingesetzt werden dürfen. Man muss also prüfen, ob durch einen bestimmten x-Wert
der Nenner eines Bruches 0 würde
etwas Negatives unter einer Wurzel stünde
das Argument eines Logarithmus kleiner oder gleich 0 wäre.
Mögliches Verhalten des Funktionsgraphen an der Definitionslücke
An einer Definitionslücke kann sich eine Polstelle, eine hebbare Definitionslücke oder eine Sprungstelle befinden.
Definitionsränder
Soll das Verhalten an den Definitionsrändern untersucht werden, so muss man das Verhalten des Graphen links und rechts der Definitionslücken betrachten sowie meistens das Verhalten des Graphen im Unendlichen. Dies funktioniert mithilfe der Grenzwertbetrachtung.
Übungsaufgaben: Definitionsbereich einer Funktion
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Bestimmung von Definitionsmengen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
