Eine Nullstelle einer Funktion ist der x-Wert eines Schnittpunktes vom Graphen von mit der x-Achse.
Das sind also gerade die -Werte, an denen ist.
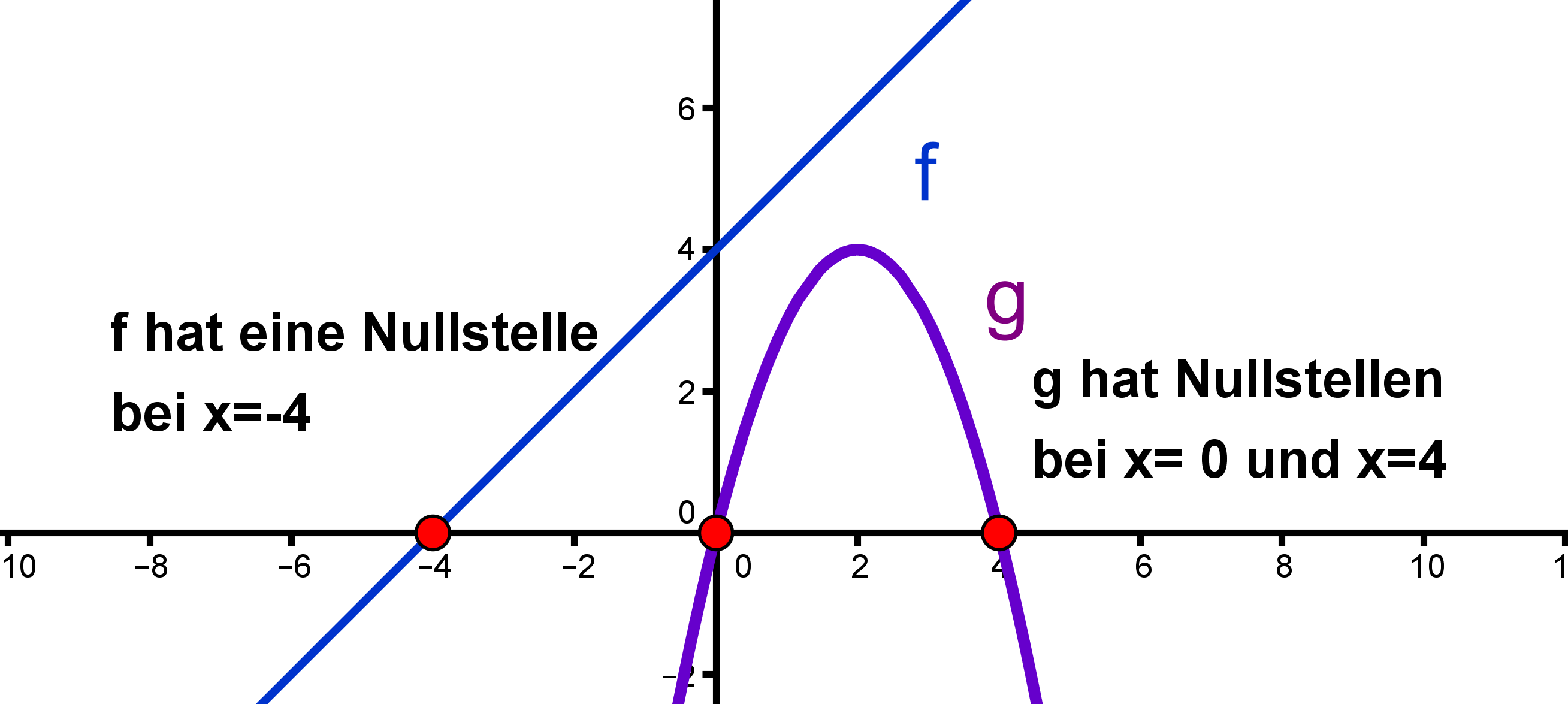
Hier sind die Nullstelle(n) der linearen Funktion mit und der quadratischen Funktion mit eingezeichnet.
Veranschaulichung an einem Applet
Nullstellen berechnen
Wie du Nullstellen berechnen kannst, wird dir im Artikel Nullstellen berechnen erklärt.
Vielfachheiten
Manchmal wirst du auch nach der Vielfachheit gefragt. Wie du diese bestimmst, kannst du im Artikel Vielfachheit von Nullstellen nachlesen.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
