Manche Schnittstellen mit der x-Achse sehen anders aus als andere. Das liegt an der Vielfachheit der jeweiligen Nullstelle.
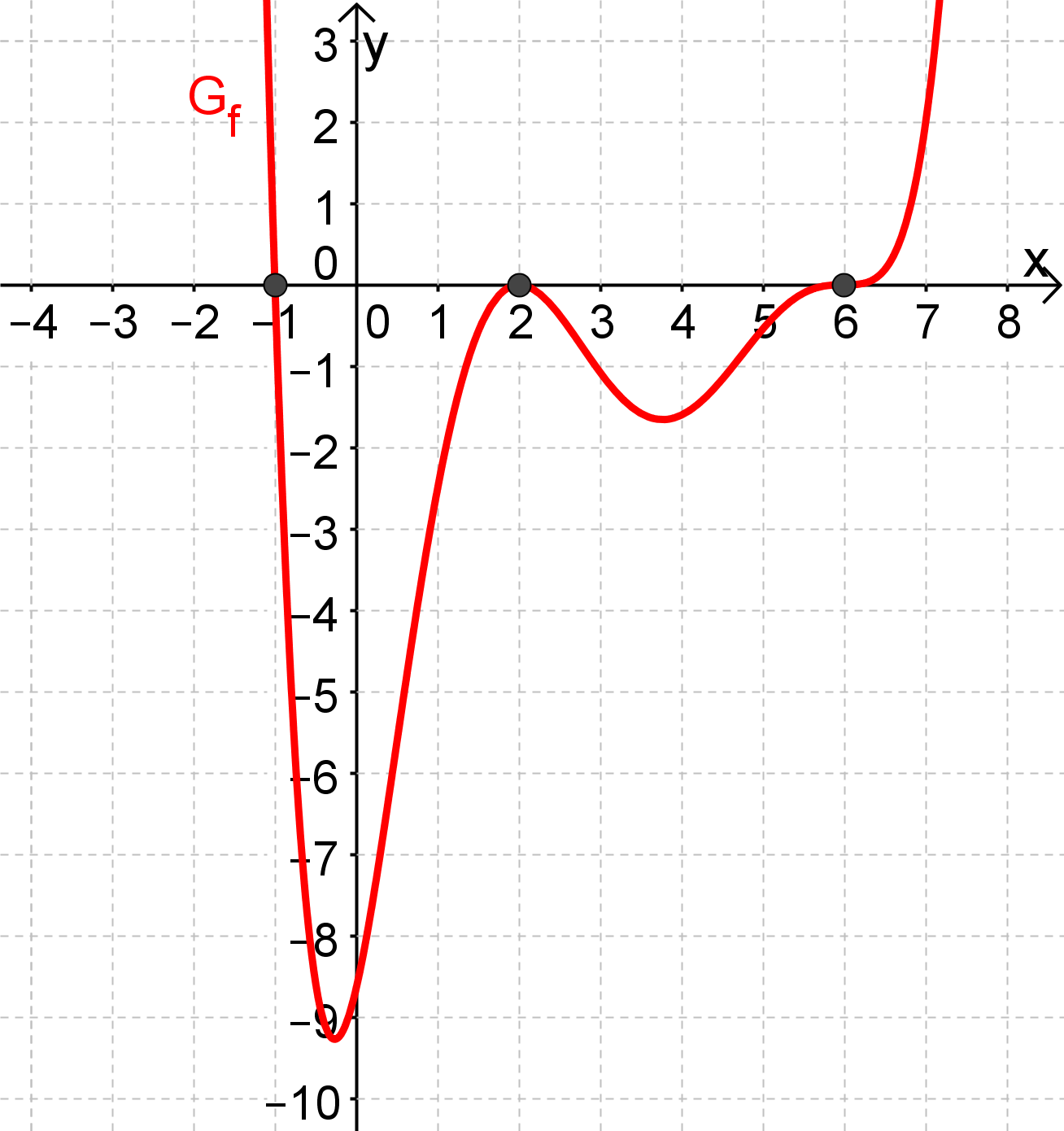
Im Graph ist zum Beispiel
eine Nullstelle mit Vielfachheit 1,
eine Nullstelle mit Vielfachheit 2 und eine Nullstelle mit Vielfachheit 3.
Vielfachheit aus dem Funktionsterm ermitteln
Berechnest du die Nullstellen einer Funktion, so kann es passieren, dass du einzelne Nullstellen mehrmals rausbekommst. Bekommst du das Ergebnis bei der Berechnung zum Beispiel zweimal heraus, so handelt es sich um eine Nullstele mit Vielfachheit 2 (oder doppelte Nullstelle).
Graphische Bedeutung der Vielfachheit
Bei Nullstellen mit geraden Vielfachheiten berührt der Graph die x-Achse, ohne dass dieser das Vorzeichen wechselt. Er "prallt" von der x-Achse ab.
Bei Nullstellen mit ungerader Vielfachheit schneidet der Graph die x-Achse. Er wechselt dort das Vorzeichen.
Je höher die Vielfachheit der Nullstelle, desto länger hält sich der Graph in der Nähe der x-Achse auf. Die Nullstelle wird zunehmend "platter".
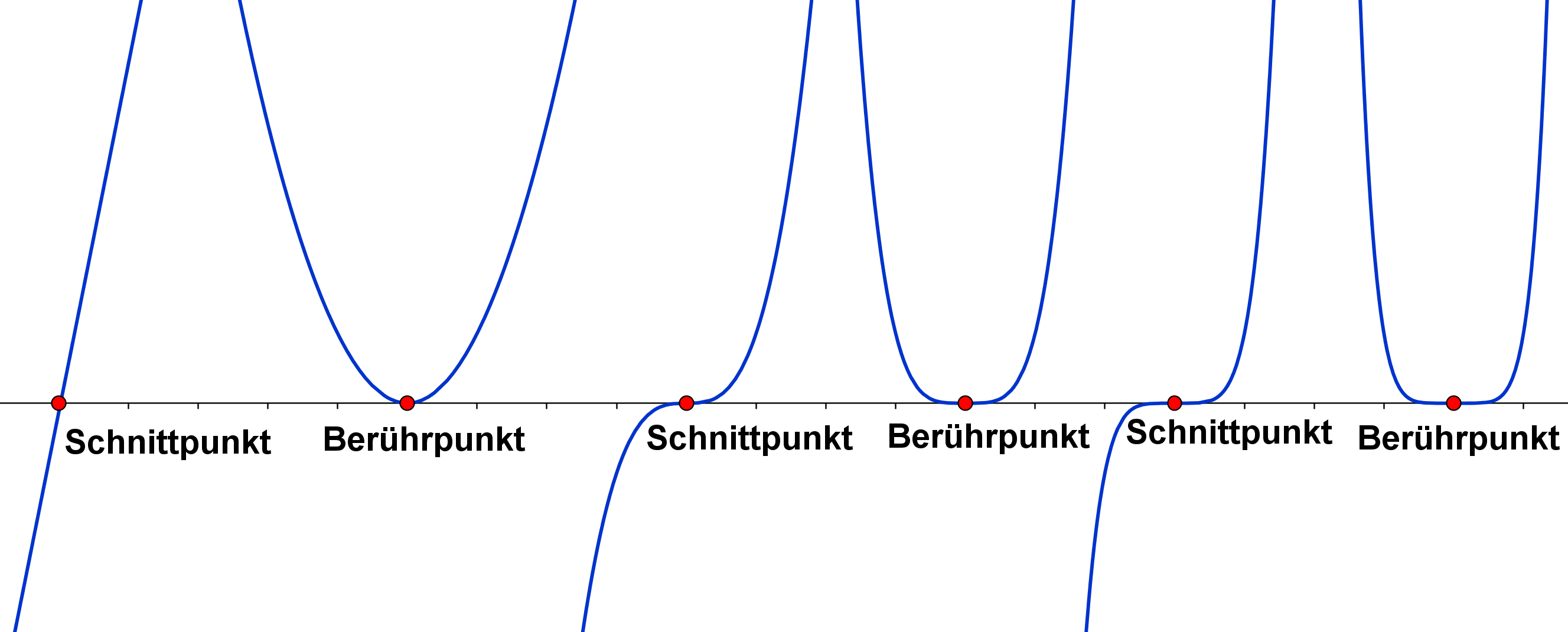
Nullstellen mit Vielfachheit 1 bis Vielfachheit 6
Laden
Übungsaufgaben: Vielfachheit von Nullstellen
Laden
