Aufgaben zu Funktionen und Relationen

Hier findest du Aufgaben zu Funktionen und Relationen. Lerne, funktionale Zusammenhänge und Funktionen zu erkennen!

1
Welche der folgenden fünf Graphen gehören sicher nicht zu einer Funktion?
$G_3$ und $G_4$
$G_1, G_3$ und $G_5$
$G_2$ und $G_4$
$G_2$ und $G_5$
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktion
Die Auswahlmöglichkeit $G_1$ , $G_3$ und $G_5$ führt zu Funktionen. Danach war aber in der Aufgabenstellung nicht gefragt.
Der Graph $G_1$ berührt die $y$ -Achse einmal im Punkt $A$ .
Jede weitere beliebige Parallele zur $y$ -Achse darf den Graphen dabei höchstens einmal schneiden; hier beispielsweise im Punkt $B$ .
$G_1$ gehört also zu einer Funktion.
Der Graph $G_3$ schneidet die $y$ -Achse einmal im Punkt $A$ .
Jede beliebige Parallele zur $y$ -Achse kann den Graphen dabei genau einmal schneiden; hier im Punkt $B$ .
$G_3$ gehört also zu einer Funktion.
Der Graph $G_5$ schneidet die $y$ -Achse einmal im Punkt $A$ .
Jede beliebige Parallele zur $y$ -Achse kann den Graphen dabei genau einmal schneiden; hier im Punkt $B$ .
$G_5$ gehört also zu einer Funktion.
Die Auswahlmöglichkeit $G_2$ und $G_4$ ist die gesuchte Antwort aus der Fragestellung.
Der Graph $G_2$ schneidet die $y$ -Achse im Punkt $A$ und im Punkt $B$ .
Damit wird aber gegen die Funktionseigenschaft verstoßen, dass jedem $x$ -Wert genau ein $y$ -Wert zugeordnet wird. $G_2$ gehört also nicht zu einer Funktion.
Der Graph $G_4$ schneidet die $y$ -Achse im Punkt $A$ und im Punkt $B$ .
Damit wird aber gegen die Funktionseigenschaft verstoßen, dass jedem $x$ -Wert genau ein $y$ -Wert zugeordnet wird. $G_4$ gehört also nicht zu einer Funktion.
Bei den Auswahlmöglichkeit $G_3$ und $G_4$ bzw. $G_2$ und $G_5$ war jeweils eine Funktion und jeweils einmal keine Funktion dabei.
Am Graphen kannst Du sehr gut ablesen, ob die Funktionseigenschaft erfüllt ist, ob also jedem $x$ -Wert genau ein $y$ -Wert zugeordnet wird. Jede Parallele zur $y$ -Achse kann den Graphen dabei genau einmal schneiden.
2
Wähle alle richtigen Aussagen aus:
Der Graph einer Funktion schneidet die $y$ -Achse höchstens einmal.
Eine zur $x$ -Achse parallele Gerade ist ein Funktionsgraph.
Der Graph einer Funktion schneidet die $x$ -Achse mindestens einmal.
Der Graph einer Funktion schneidet die $x$ -Achse höchstens einmal.
Der Graph einer Funktion schneidet die $y$ -Achse mindestens einmal.
Eine zur $y$ -Achse parallele Gerade ist ein Funktionsgraph.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen
Bei dieser Aufgabe sind sechs Aussagen angegeben, von denen man jeweils herausfinden soll, ob sie richtig sind.
Beachte dabei: Du darfst eine Aussage nur dann als richtig werten, wenn sie auch wirklich immer stimmt, und nicht schon dann, wenn es irgendwelche Fälle gibt, in denen sie mal richtig ist.
Sobald es auch nur ein einziges Gegenbeispiel gibt, ist die Aussage falsch.
Wahr sind nur die Aussagen, die "im allgemeinen Fall" richtig sind.
Falsche Aussagen
Folgende Aussagen sind für den allgemeinen Fall nicht richtig:
"Der Graph einer Funktion schneidet die $x$ -Achse mindestens einmal."
"Der Graph einer Funktion schneidet die $x$ -Achse höchstens einmal."
"Der Graph einer Funktion schneidet die $y$ -Achse mindestens einmal."
Und die folgende Aussage ist sogar immer falsch:
"Eine zur $y$ -Achse parallele Gerade ist ein Funktionsgraph."
Richtige Aussagen
Richtig sind die folgenden Aussagen:
"Eine zur $x$ -Achse parallele Gerade ist ein Funktionsgraph."
"Der Graph einer Funktion schneidet die $y$ -Achse höchstens einmal."
Begründungen
Zur Aussage "Der Graph einer Funktion schneidet die x-Achse mindestens einmal."
Betrachte zum Beispiel den folgenden Funktionsgraphen:
Dieser Graph schneidet die $x$ -Achse nicht.
Anmerkung:
Die Funktion, zu der der Graph im Bild gehört, ist: $f:x \mapsto 0{,}5x²+1$
Die Aussage ist also im Allgemeinen falsch, da es eine Funktion gibt, für die sie nicht erfüllt ist.
("Im Allgemeinen falsch" heißt: Für eine bestimmte Funktion kann sie schon richtig sein, aber sie stimmt nicht für jede Funktion, also nicht "allgemein").
Zur Aussage "Der Graph einer Funktion schneidet die $x$ -Achse höchstens einmal."
Betrachte zum Beispiel den folgenden Funktionsgraphen:
Dieser Graph schneidet die $x$ -Achse mehr als einmal.
Anmerkung:
Die Funktion, zu der der Graph im Bild gehört, ist: $g:x \mapsto x²-2$
Die Aussage ist also im Allgemeinen falsch, da es eine Funktion gibt, für die sie nicht erfüllt ist.
Zur Aussage "Der Graph einer Funktion schneidet die $y$ -Achse mindestens einmal."
Betrachte zum Beispiel den folgenden Funktionsgraphen:
Dieser Graph hat keinen Schnittpunkt mit der $y$ -Achse. da der $x$ -Wert $0$ nicht im Definitionsbereich der Funktion ist.
Anmerkung:
Die Funktion, zu der der Graph im Bild gehört, ist: $h:x \mapsto \frac{1}{x}$
Die Aussage ist also im Allgemeinen falsch, da es eine Funktion gibt, für die sie nicht erfüllt ist.
Zur Aussage "Eine zur $y$ -Achse parallele Gerade ist ein Funktionsgraph."
Betrachte zum Beispiel den folgenden Graphen:
Dieser Graph gehört nicht zu einer Funktion.
Eine zur $y$ -Achse parallele Gerade kann nicht Graph einer Funktion sein, weil diese Funktion dann einem einzigen $x$ -Wert unendlich viele $y$ -Werte (und nicht nur einen!) zuordnen würde.
Die Aussage ist sogar immer falsch, es gilt nämlich:
Eine zur y-Achse parallele Gerade ist kein Graph einer Funktion $f: x\mapsto f(x)$ .
Zur Aussage "Eine zur $x$ -Achse parallele Gerade ist ein Funktionsgraph."
Diese Aussage ist richtig.
Wenn eine Gerade parallel zur $x$ -Achse bei $y=a$ verläuft, dann haben alle ihre Punkte den $y$ -Wert $a$ .
Daher ist die Gerade Graph der Funktion
$f:x\mapsto a$ ,
die jedem $x$ den Wert $a$ zuordnet.
(Die Gerade im Bild hier zum Beispiel ist Graph der Funktion $f: x\mapsto 1$ . )
Zur Aussage "Der Graph einer Funktion schneidet die $y$ -Achse höchstens einmal."
Die Aussage ist richtig.
Wenn ein Graph die $y$ -Achse mehr als einmal schneidet, kann er nicht Graph einer Funktion $f: x \mapsto f(x)$ sein.
Denn dem $x$ -Wert $x=0$ müsste dann mehr als nur ein $y$ -Wert zugeordnet sein.
3
Zeichne die Graphen folgender Relationen und untersuche, ob es sich um Funktionen handelt:
1. Die folgende Relation $R\subseteq \mathbb{N} \times \mathbb{N}$ ist folgendermaßen definiert:
  $R = \{ (x, y) \mid y$ ist Nachfolger von $x \}$
  Ist $R$ eine Funktion?
  Ja
  Nein
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relationen
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Ja, denn jedes Element $n \in \mathbb{N}$ hat einen eindeutig bestimmten Nachfolger. Zum Beispiel hat die natürliche Zahl 1 den Nachfolger 2, die 2 die 3 usw.
2. Die Relation $R \in \mathbb{N} \times \mathbb{N}$ ist folgendermaßen definiert:
  $R = \{(x, y) \mid y$ ist Vorgänger von $x \}$
  Ist R eine Funktion?
  Ja
  Nein
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relationen
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Nein, R ist keine Funktion. Denn die Zahl 1 hat keinen Vorgänger. Die Funktion ist also nicht total definiert.
3. $f=\left\{\left(x\vert y\right)\vert x^2+y^2=4 \wedge x\in\left[-2;2\right]\right\}$
  Ist $f$ eine Funktion?
  Ja
  Nein
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relationen
  Dies ist ein Kreis um (0|0) mit Radius r = 2. Deshalb gibt es für x= 0 zwei y-Werte, woraus folgt, dass f keine Funktion ist.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $f=\left[2;5\left[\, \times\, \right]1;3\right]$
  Ist $f$ eine Funktion?
  Ja
  Nein
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Relationen
  Wäre f eine Funktion, müsste es für jedes x genau ein y geben. Hier ist das Kreuzprodukt zweier Mengen gegeben. Beim Kreuzprodukt wird jedes x mit jedem y kombiniert, also gibt es für jedes x mehrere y.
  Es ist also eine Relation, aber keine Funktion.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Begründe, ob es sich bei der gegebenen Relation $f$ um eine Funktion handelt und beantworte die Zusatzfragen.

\displaystyle f

=

\displaystyle \left\{\left(x\vert y\right)\;\vert\;x^2=y^2\;;\;{\mathit D}_\mathit f=\left[-2{,}2\right]\right\}

Zusatzfrage: Zeichne den Graphen zu der Funktion.

\displaystyle f

=

\displaystyle \left\{\left(x\vert y\right)\;\vert\;x=y^3\;;\;{\mathit W}_\mathit f=\left[-2;2\right]\right\}

Zusatzfrage 1: Wie lautet der Definitionsbereich von $f$ ?

Zusatzfrage 2: Für welches x ist $f\left(x\right)=1{,}2$ ?

5
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Gegeben ist die Punktemenge $A=\left\{\left(\left.1\;\right|\;3\right);\left(\left.2\;\right|\;\frac32\right);\;\left(\left.3\;\right|\;1\right);\;\left(\left.4\;\right|\;\frac34\right);…\;\right\}$
Geben Sie drei weitere Elemente von $A$ an und tragen Sie die Punkte in ein Koordinatensystem ein. Gibt es einen Zusammenhang zwischen $x$ - und $y$ - Koordinate?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Relationen
Gegeben sind die Punkte $A(1\vert3)$ , $B(2\vert\dfrac{3}{2})$ , $C(3\vert1)$ und $D(4\vert\dfrac{3}{4}).$
Schreibst Du die $y$ -Werte der Punkte $A$ und $C$ als unechte Brüche, so erhälst Du die folgende Darstellung: $A(1\vert\dfrac{3}{1})$ , $B(2\vert\dfrac{3}{2})$ , $C(3\vert\dfrac{3}{3})$ und $D(4\vert\dfrac{3}{4})$ .
Gesucht sind drei weitere Punkte, die zu der Menge $A$ gehören.
Bei allen Punkten erkennst Du jeweils eine $3$ im Zähler des Bruches des $y$ -Wertes. Bei allen Punkten ist außerdem der $x$ -Wert des Punktes gleich dem Nenner des Bruches des $y$ -Wertes.
Somit könnten weitere Punkte mit folgenden Koordinaten zur Menge $A$ gehören:
$E(5\vert\dfrac{3}{5})$ , $F(6\vert\dfrac{3}{6})$ und $G(7\vert\dfrac{3}{7})$
Abbildung der Punkte $A$ bis $G$ im Koordinatensystem.
In der Aufgabe war nach einem Zusammenhang zwischen der $x$ - und $y$ - Koordinate gefragt.
Vermutet wird ein funktionaler Zusammenhang: $f(x)= \dfrac{3}{x}$ .
Trägt man diese Funktion in das obige Koordinatensystem ein, erkennt man, dass alle Punkte auf dem Funktionsgraphen liegen.
Antwort: Die Punkte $E$ , $F$ und $G$ gehören zu der Menge A und es gibt einen funktionalen Zusammenhang zwischen der $x$ - und $y$ - Koordinate: $f(x)= \dfrac{3}{x}$ .
Es handelt sich hier um eine mit dem Faktor $3$ in $y$ -Richtung gestreckte Hyperbel.
6
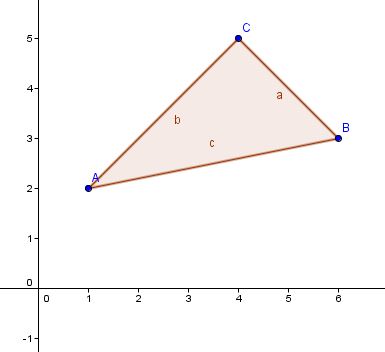
Der Graph der Relation f ist die Fläche des Dreiecks ABC mit A( 1 | 2 ), B( 6 | 3 ) und C( 4 | 5 ). Die Seite [AB] gehört zum Graphen, die beiden anderen Seiten nicht. Schreiben Sie f als Menge hin.
Für diese Aufgabe benötigst Du folgendes Grundwissen: Relationen
Um das Dreieck als Menge zu schreiben, zeichne zuerst das Dreieck in ein Koordinatensystem, um herauszufinden welche Werte x und y annehmen darf.
Nun siehst du an dieser Zeichnung, dass der Funktionswert zwischen den drei Geraden liegen soll, die die Seiten des Dreiecks darstellen.
Stellst du diese drei Geradengleichungen auf, so bekommst du:
[AB]= $\frac{1}{5}x+ \frac{9}{5}$
[BC]= $-x+9$
[AC]= $x+1$
Also erhälst du für die Mengenschreibweise:
$f=\{ y \geq \frac{1}{5}x+ \frac{9}{5} \wedge y < -x+9 \wedge y<x+1\}$
Das $\geq$ in der ersten Bedingung der Menge kommt daher, dass die Seite [AB] zu der Menge dazugehören soll. Bei den anderen beiden Bedingungen schreibt man deswegen ein <, da die Seiten nicht dazugehören sollen.
7
Der Graph der Relation f ist eine offene Kreisscheibe (ohne Rand) um den Mittelpunkt M( 1 | 2 ) mit dem Radius r = 3. Schreiben Sie f als Menge hin.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Kreise
Ein Kreis lässt sich in der Mengenschreibweise darstellen als $\{(x|y)|(x-x_M)^2+(y-y_M)^2 < r^2 \}$
Also lässt sich der gegebene Kreis darstellen als:
$f=\left\{(x\vert y\right) \vert \left(x-1\right)^2+ \left(y-2 \right)^2 < 9 \}$
8
Gegeben sind
$F=\left\{x\vert x\in ℕ\;\mathrm{und}\;1\leq x\leq80\right\},\\G=\left\{x\vert x\in\mathbb{N}_0\;\mathrm{und}\;0\leq x\leq\mathrm{180}\right\}.\\$
Wie viele Elemente besitzen die Mengen
$H=F\times\left(G\times F\right)$ und
$K=G\times \left(G\times F\right)$ ?
Für diese Aufgabe benötigst Du folgendes Grundwissen: Mächtigkeit
1) Die Anzahl der Elemente des kartesischen Produkts lässt sich durch Multiplikation der einzelnen Mächtigkeiten der Mengen berechnen. $|H|=|F|\cdot |G| \cdot |F| =80 \cdot 181 \cdot 80 =1.158.400$
2) Auch hier lässt sich die Anzahl der Elemente auf die gleiche Weise berechnen. $|K|= |G| \cdot |G| \cdot |F|= 181 \cdot 181 \cdot 80 = 2.620.880$
9
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Gegeben ist der Punkt $P\left(\left.t\;\right|\;\frac t2+3\right)$ mit $t\in\mathbb{R}$
Wählen Sie für t einige Werte und tragen Sie die dazugehörigen Punkte in ein Koordinatensystem ein.
Wie liegen die Punkte im Koordinatensystem? Für welche t- Werte gilt: x- Koordinate ist gleich y- Koordinate des Punktes P?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Punkte in ein Koordinatensystem zeichnen
Setze beispielsweise $t=\left\{0;1;2;3;4\right\}$ ein und berechne die zugehörigen y-Werte. Auch andere Zahlen für $t$ sind zulässig.
$t=0:\;y=\frac02+3$
$\hphantom{t=0:.;}y=3$
$\Rightarrow\;A(0\;|\;3)$
$t=1:\;y=\frac12+3$
$\hphantom{t=1::.}y=3{,}5$
$\Rightarrow\;B(1\;|\;3{,}5)$
$t=2:\;y=\frac22+3$
$\hphantom{t=2;;.}y=4$
$\Rightarrow\;C(2\;|\;4)$
$t=3:\;y=\frac32+3$
$\hphantom{t=3::.}y=4{,}5$
$\Rightarrow\;D(3\;|\;4{,}5)$
$t=4:\;y=\frac42+3$
$\hphantom{t=4;;.}y=5$
$\Rightarrow\;E(4\;|\;5)$
Zeichne die Punkte A, B, C, D und E in ein Koordinatensystem.
$\;\;\Rightarrow\;\;$ Alle Punkte liegen auf einer Geraden. Diese hat die Gleichung $y=\dfrac t2+3$ .
Berechne, wann die x - und y - Koordinate den gleichen Wert haben.
Setze dafür y mit t gleich.
$t=y$
Ersetze $y$ durch den Term $\dfrac t2+3$ .
$t=\dfrac t2+3 \qquad \qquad \left|\cdot2\right.$
$2t=t+6 \qquad \qquad \left|-t\right.$
$t=6$
$\;\;\Rightarrow\;\;$ Die x - und y - Koordinate haben den gleichen Wert, wenn $t= 6$ ist. Der zugehörige Punkt ist $P\left(6\;|\;6\right)$ .
10
Handelt es sich um eine Funktion oder nur um eine Zuordnung?
1. Einer Sängerin hat besonders erfolgreiche Lieder, auch Nummer 1 Hits genannt. Jedem Jahr wird die Anzahl dieser Nummer 1 Hits zugeordnet.
  eine Funktion
  nur eine Zuordnung
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen
  Zu jedem Jahr gibt es eine eindeutige Zahl an Nummer 1 Hits. Deshalb handelt es sich um eine Funktion
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Diesmal wird die umgedrehte Richtung angeschaut:
  Anzahl der Nummer 1 Hits $\mapsto$ Jahr
  Es ist eine Funktion
  Es ist nur eine Zuordnung
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen
  Dies ist nur eine Zuordnung. 0 Hits hat sie zum Beispiel in jedem Jahr, in dem sie keine Musik produziert.
  Es gibt also keinen eindeutigen Wert, der der Anzahl 0 Hits zugeordnet wird und deshalb ist es nur eine Zuordnung, keine Funktion
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Du kaufst Äpfel und zahlst jeden einzelnen davon. Die betrachete Zuordnung ist: Anzahl Äpfel $\mapsto$ Preis
  Es ist eine Funktion
  Es handelt sich nur um eine Zuordnung
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen
  Es handelt sich um eine Funktion, denn jeder Stückzahl kann an diesem Tag eindeutig der zugehörige Preis zugeordnet werden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. Wieder kaufst du Äpfel. Diesmal interessiert dich aber der Zusammenhang Preis $\mapsto$ Anzahl Äpfel
  Es handelt sich um eine Funktion
  Es ist lediglich eine Zuordnung
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Funktionen
  Auch dies ist eine Funktion. Zahlt man einen bestimmten Preis bekommt man an diesem Tag dafür auch immer eine bestimmte Anzahl an Äpfeln
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉

Damit Familie Dippet an Halloween nicht permanent an die Tür muss, um den Kindern Süßigkeiten zu geben, haben sie vor ihrer Tür ein Glas mit 200 Süßigkeiten aufgestellt. Sven ist neugierig und läuft immer wieder zum Türspion, um zu schauen, wie voll das Glas noch ist.

Er stellt fest: "Jede Stunde werden es genau 25 Stück weniger!"

Begründe, warum es sich bei der Zuordnung Zeit in Stunden $\mapsto$ Menge der Süßigkeiten um eine Funktion handelt.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Was ist eine Funktion?
Es handelt sich um eine Funktion, denn zu jedem Zeitpunkt gibt es genau eine Anzahl an Süßigkeiten.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Bei einer Funktion wird jedem x aus der Definitionsmenge X genau einem y aus der Wertemenge y zugeordnet. Es darf also für keinen x-Wert mehrere oder keine y-Werte geben.
Es handelt sich um eine lineare Funktion. Finde eine Funktionsgleichung zu dieser Situation.

Für diese Aufgabe benötigst Du folgendes Grundwissen: lineare Funktion
Der y-Achsenabschnitt liegt bei 200, da dies die maximale Anzahl der Süßigkeiten ist bzw. die Anfangsanzahl. -25x, da es jede Stunde 25 Stück weniger wird.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Welche Bedeutung haben y-Achsenabschnitt und Steigung in dieser Situation?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Was ist eine Funktion
Steigung: -25x, da es jede Stunde 25 Stück weniger wird,
y-Achsenabschnitt: 200 für den Anfangsmenge der Süßigkeiten
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Ludwig meint: "Ich glaube nach 3,5 Stunden sind noch 145 Süßigkeiten im Glas". Stimmt das?
- Richtig
- Falsch
Setze den Zeitpunkt 3,5 für x in die Funktionsgleichung ein:
$y=-25\ \cdot3{,}5\ +200=112{,}5$
Nach 3,5 Stunden sind also ca 112 Stücke im Glas, nicht 145
Hast du eine Frage oder Feedback?
Kommentiere hier 👉
Ina sagt: "Nach 5 Stunden sind sicher nur noch 100 oder weniger Süßigkeiten im Glas". Hat sie Recht?
- Ja, hat sie
- Nein, hat sie nicht
Für diese Aufgabe benötigst Du folgendes Grundwissen: Was ist eine Funktion
Setze 5 für x in den Funktionsterm ein.
$f\left(5\right)=-25\cdot5+200=75$
Sie hat also recht, denn es sind weniger als 100 Süßigkeiten im Glas.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Sven überlegt: "Aber nach wie vielen Stunden ist das Glas leer, wenn es draußen so weitergeht?" Bestimme diesen Zeitpunkt!

12
Familie Kwo hat um 17 Uhr ein Glas mit Süßigkeiten aufgestellt. Die Anzahl der vorhandenen Süßigkeiten in Abhängigkeit von der vergangenen Zeit in Stunden lässt sich mit folgendem Graphen darstellen:
1. Wie häufig wurde bei der Erstellung des Graphen die Menge der Süßigkeiten erfasst?
  10 mal
  12 mal
  20 mal
  15 mal
  
  Zählt man alle Punkte zwischen 0 und 7, so kommt man auf 15 Stück, also 15 Messungen.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Jeder Punkt, der im Graphen durch ein kleines x markiert ist, entspricht einer Messung.
2. Beschreibe, wie sich die Menge der Süßigkeiten im Verlauf des Abends entwickelt.
  
  Um 17 Uhr enthält das Glas 60 Süßigkeiten.
  In der ersten halben Stunde werden keine Süßigkeiten entnommen.
  Nach einer Stunde sind noch 30 Süßigkeiten im Glas,
  nach 1,5 Stunden noch 10.
  Das Glas wird nun wieder aufgefüllt, so dass nach 2 Sunden 90 Süßigkeiten im Glas sind. Nach 2,5 Stunden sind 40 Süßigkeiten im Glas,
  nach 3 Stunden 20 und
  nach 3,5 Stunden ist das Glas leer.
  Nun wird das Glas wieder aufgefüllt und enthält nach 4 Stunden wieder 60 Süßigkeiten,
  nach 4,5 Stunden sind es 40,
  nach 5 Stunden 30,
  nach 5,5 Stunden 26 und
  nach 6 Stunden 24 Süßigkeiten.
  Nach 6,5 Stunden enthält das Glas 20 und
  nach 7 Stunden ebenfalls 20 Süßigkeiten.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. Erkläre, warum es sich bei Familie Kwo und der Zuordnung Süßigkeitenmenge $\mapsto$ Uhrzeit nicht um eine Funktion handelt.
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Was ist eine Funktion
  Es handelt sich nicht um eine Funktion, da die Anzahl der Süßigkeiten nicht eindeutig einem Zeitpunkt zugeordnet werden kann. Nach 3 und nach 6 Stunden gibt es zum Beispiel die gleiche Menge Süßigkeiten im Glas.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
  Bei einer Funktion darf es zu jedem x der Definitionsmenge nur ein y der Wertemenge geben.
13
Ordne den Sätzen die entsprechende Zuordnungsvorschrift zu.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Was ist eine Funktion?

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle 0$	$=$	$\displaystyle -25x\ +200$	$\displaystyle -200$
	↓	Bringe 200 durch - auf die andere Seite
$\displaystyle -200$	$=$	$\displaystyle -25x$	$\displaystyle :\left(-25\right)$
	↓	Teile -200 durch :(-25)
$\displaystyle 8$	$=$	$\displaystyle x$

Aufgaben zu Funktionen und Relationen

Falsche Aussagen

Richtige Aussagen

Begründungen

Zur Aussage "Der Graph einer Funktion schneidet die ﻿x-Achse mindestens einmal."

Zur Aussage "Der Graph einer Funktion schneidet die xxx-Achse höchstens einmal."

Zur Aussage "Der Graph einer Funktion schneidet die yyy-Achse mindestens einmal."

Zur Aussage "Eine zur yyy-Achse parallele Gerade ist ein Funktionsgraph."

Zur Aussage "Eine zur xxx-Achse parallele Gerade ist ein Funktionsgraph."

Zur Aussage "Der Graph einer Funktion schneidet die ﻿yyy-Achse höchstens einmal."

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Zur Aussage "Der Graph einer Funktion schneidet die x-Achse mindestens einmal."

Zur Aussage "Der Graph einer Funktion schneidet die $x$ -Achse höchstens einmal."

Zur Aussage "Der Graph einer Funktion schneidet die $y$ -Achse mindestens einmal."

Zur Aussage "Eine zur $y$ -Achse parallele Gerade ist ein Funktionsgraph."

Zur Aussage "Eine zur $x$ -Achse parallele Gerade ist ein Funktionsgraph."

Zur Aussage "Der Graph einer Funktion schneidet die $y$ -Achse höchstens einmal."