Lineare Funktion

Eine lineare Funktion hat die Form $f(x)=m\cdot x+b$. Ihr Graph ist eine Gerade.

Der Graph einer linearen Funktion sieht zum Beispiel für $f(x)=2x+4$ so aus:

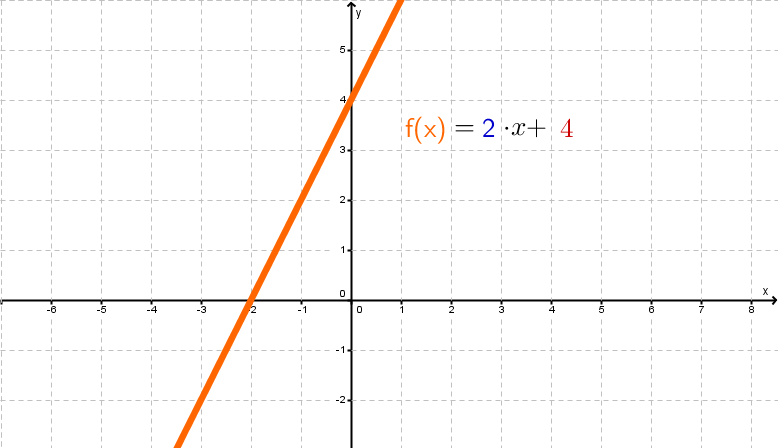
Die Steigung m

Die Zahl $m$ vor der Variablen $x$ gibt die Steigung der Funktion an.

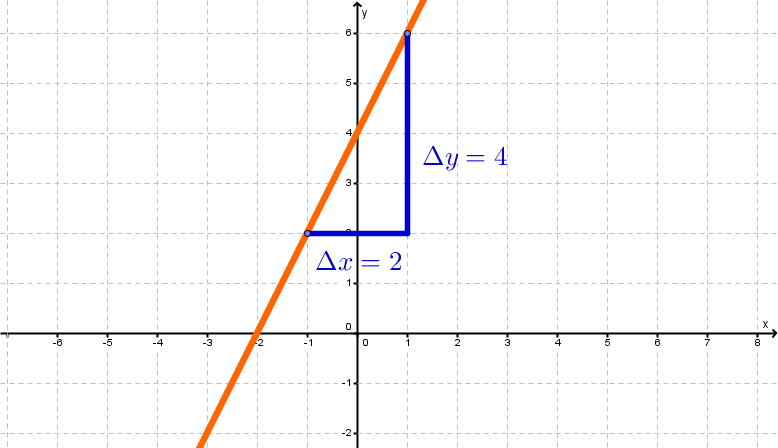
Die Steigung kann man an dem Graphen anhand des Steigungsdreiecks ablesen:

Der y-Achsenabschnitt b

Die Zahl $b$ gibt den $y$-Achsenabschnitt der Funktion an. Der $y$-Achsenabschnitt ist der Funktionswert bei $x=0$.

Oft wird statt dem $b$ auch ein $n$ oder ein $t$ benutzt.

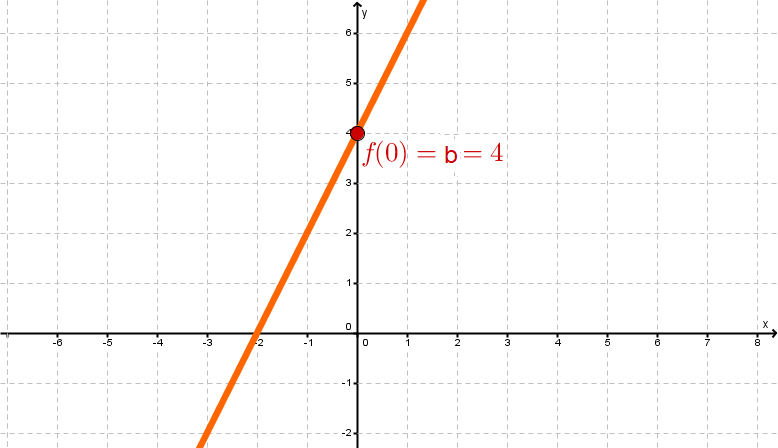
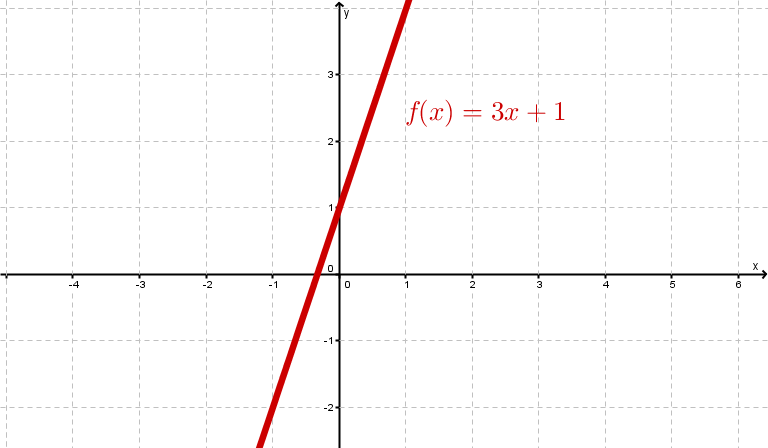
Beispiele

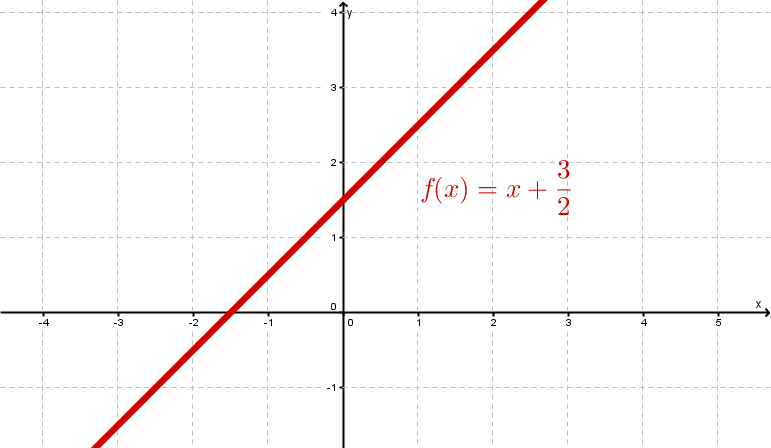
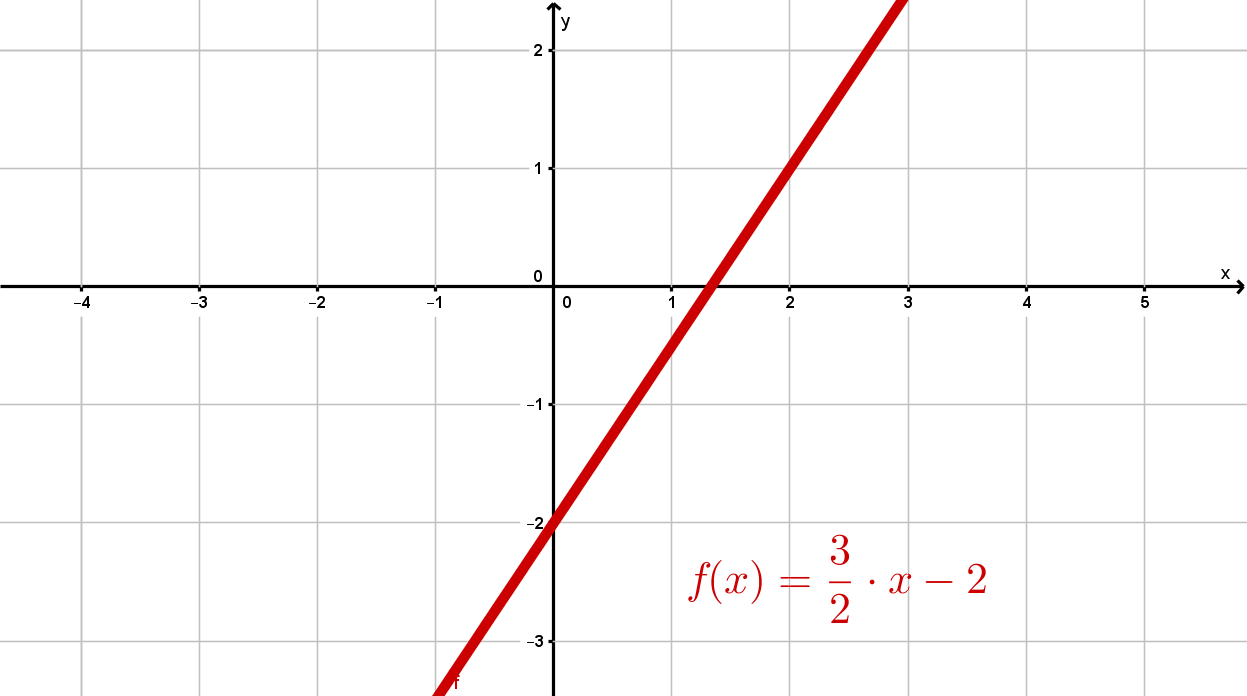
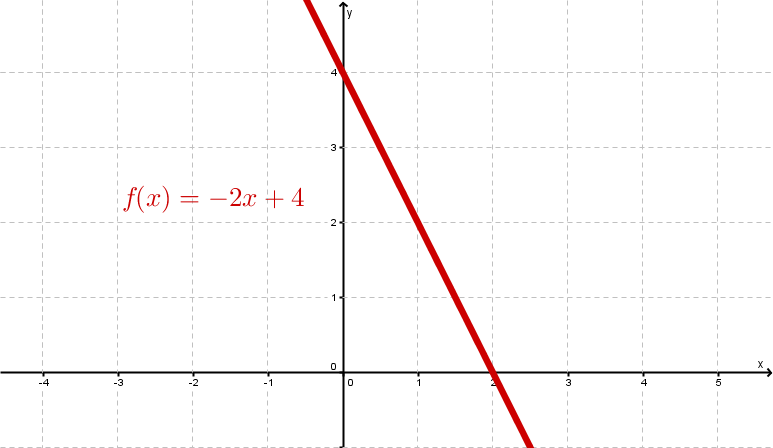
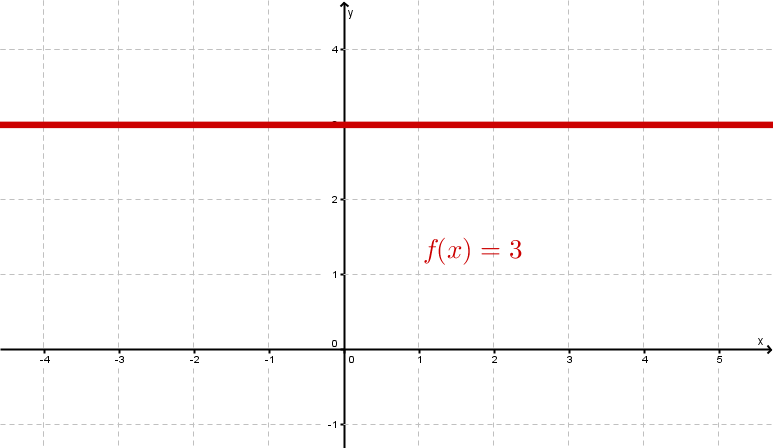
Video zum Thema „Lineare Funktionen“