Wendepunkte und Terrassenpunkte

In diesem Artikel lernst du die Eigenschaften von Wendepunkten und deren Spezialfällen, den Sattel- bzw. Terrassenpunkten, kennen.

Ein Wendepunkt $P\left(x_P\mid f(x_P)\right)$ ist ein Punkt auf einem Funktionsgraphen, an dem sich die Krümmungsrichtung des Graphen ändert. Ist die Tangente durch diesen Punkt horizontal, so nennen wir ihn einen Terrassen- oder Sattelpunkt.

Anmerkung: In diesem Artikel wird $f$ als dreimal differenzierbar angenommen.

Wendepunkt

Definition

Ein Wendepunkt (WP) einer Funktion $f$ ist ein Punkt, an dem sich die Krümmungsrichtung des Graphen von $f$ ändert.

Dies ist gleichbedeutend dazu, dass sich das Vorzeichen der zweiten Ableitung in $x_0$ ändert.

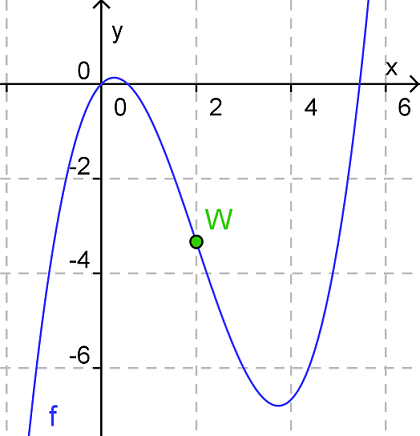
Berechnung

Notwendiges Kriterium

Für jeden Wendepunkt $x_0$ einer Funktion $f$ gilt, dass $f''(x_0)=0$ . Die zweite Ableitung von $f$ gleich null zu setzen, liefert also Kandidaten für Wendepunkte.

Beachte

Wenn man weiß, dass die zweite Ableitung einer Funktion $f$ an der Stelle $x_0$ gleich null ist, kann man nicht darauf schließen, dass $f$ dort einen Wendepunkt hat. Als Beispiel betrachten wir $f(x)=x^4$ . Die zweite Ableitung ist von der Form $f''(x)=12 \cdot x^2$ . Bei $x_0=0$ hat $f''$ eine Nullstelle, allerdings hat $f$ keinen Wendepunkt bei null.

Hinreichendes Kriterium

Wenn

$f''(x_0)=0$ und zusätzlich
$f'''(x_0)\neq 0$

gelten, dann besitzt $f$ an der Stelle $x_0$ einen Wendepunkt.

Beachte

Gelten diese Bedingungen nicht, so schließt dies nicht aus, dass bei $x_0$ ein Wendepunkt vorliegt. Zum Beispiel hat $f$ , gegeben durch $f(x)=x^5$ einen Wendepunkt bei $x_0=0$ , allerdings ist $f'''(0)=60\cdot0^2=0$ .

Vorgehen

Um die Wendepunkte nun tatsächlich zu berechnen, geht man wie folgt vor:

Berechne die ersten 3 Ableitungen $f'$ , $f''$ und $f'''$ von $f$ .
Finde alle Nullstellen $x_i$ von $f''$ .
Für jede Nullstelle $x_i$ von $f''$ prüfe, ob $f'''(x_i) \neq 0$ .
- Wenn ja $\Rightarrow x_i$ ist ein Wendepunkt.
- Wenn nicht: Prüfe, ob $f''$ bei $x_0$ das Vorzeichen wechselt.
Gib die Wendepunkte in der Form $P_i\left(x_i \mid f(x_i)\right)$ an.

Terrassenpunkt oder Sattelpunkt

Definition

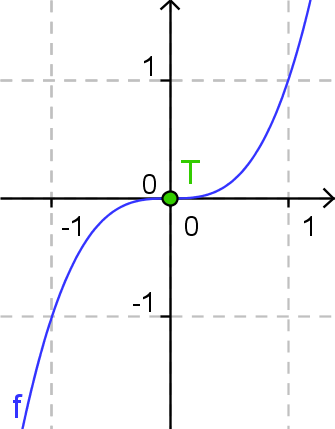
Ein Terrassenpunkt (TEP) oder Sattelpunkt (STP) ist ein Wendepunkt, in dem die Steigung einer Funktion $0$ wird.

Berechnung

Zusätzlich zu den Bedingungen des Wendepunkts ist bei einem Terrassenpunkt auch noch die erste Ableitung $0$ .

$f'(x_\mathrm{STP})=0$
$f''(x_\mathrm{STP})=0$
$f''$ wechselt bei $x_\mathrm{STP}$ das Vorzeichen (gilt z.B., wenn $f'''(x_\mathrm{STP})\neq0$ )

Übungsaufgaben: Wendepunkte und Terrassenpunkte

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zur Berechnung von Wendepunkten und Bestimmung des Krümmungsverhaltens

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?