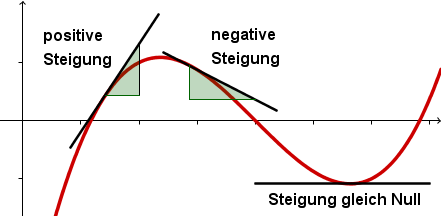
Die Ableitung einer Funktion an einer Stelle gibt die Steigung des Graphen der Funktion an dieser Stelle an.
Bezeichnet wird sie zumeist mit .

Ist , so steigt der Graph von an der Stelle .
Ist , so fällt der Graph von an der Stelle .
An den Extremstellen der Funktion und an Terrassenpunkten gilt:
.
Die Ableitung spielt daher eine wichtige Rolle bei der Berechnung der Extrema und bei der Untersuchung der Monotonie einer Funktion.
Funktionen, die an jeder Stelle der Definitionsmenge eine Ableitung besitzen, nennt man differenzierbar. Das Berechnen der Ableitung nennt man Differenzieren.
Für die Berechnung der Ableitung existieren entsprechende Ableitungsregeln.
Definition
Die Ableitung an einem Punkt
Die Ableitung ist zunächst nur für einen Punkt auf dem Graphen einer Funktion bzw. für eine Stelle definiert. Sie ist gegeben durch
oder alternativ
Anschaulich erhält man durch den Differenzenquotienten die Steigung der Sekante durch den Punkt und einen anderen Punkt auf dem Funktionsgraphen. Die Idee bei beiden Definitionen ist, dass man die Tangente durch Sekanten annähert, indem man den x-Wert des zweiten Punktes immer näher an wählt.
Was bedeutet diese Definition anschaulich?
Die Bilderfolge veranschaulicht die Bildung des Grenzwerts mit der Definition
Im Folgenden wird die Ableitung der Funktion an der Stelle berechnet. Der Punkt ist der entsprechende Punkt auf dem roten Funktionsgraphen.
Nun wähle man einen zweiten Punkt , dessen x-Koordinate um größer ist als , also . Dieser Punkt besitzt also die Koordinaten . Durch diese zwei Punkte und lässt sich die zugehörige Sekante bestimmen.
Wird nun der Punkt auf dem Graphen in Richtung von "geschoben" (d.h. die x-Koordinate von immer weiter an die x-Koordinate von angenähert, also immer weiter verringert), so wird die Sekante im Grenzfall zur Tangente. Die mithilfe des Differenzenquotienten ermittelbare Sekantensteigung wird somit zur Tangentensteigung, die wiederum dem Wert der Ableitung der Funktion an der Stelle entspricht.
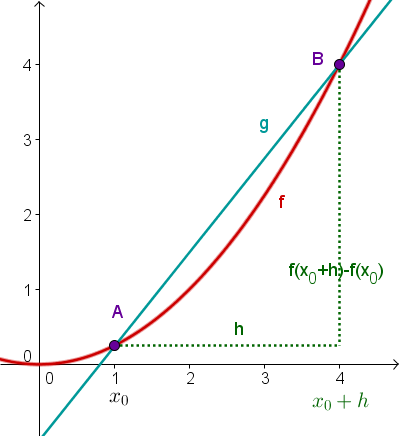
und liegen weit auseinander. Die türkise Gerade schneidet gut sichtbar den roten Graphen. Man erhält also eine Sekante.
Die Steigung der Sekante ist mit einem Steigungsdreieck (vgl. Differenzenquotient) zu bestimmen.
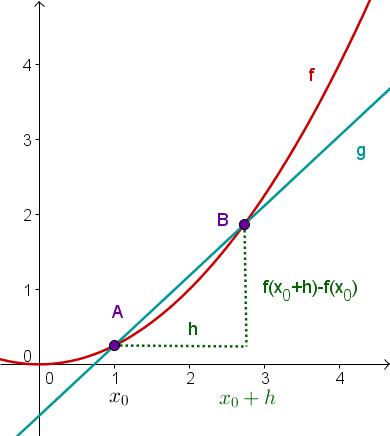
Nun wird der Grenzwert gebildet.
bedeutet, dass der Wert von immer kleiner wird. Das bedeutet wiederum, dass und , also und immer näher aneinander kommen, bis…
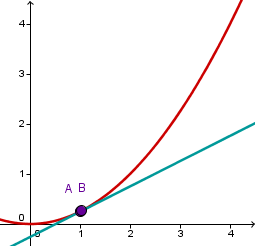
… die Differenz ganz verschwindet, also ist. Die türkise Gerade berührt den roten Graphen an dieser Stelle. Wir bekommen also eine Tangente.
Die Steigung dieser Tangente ist gleich der Ableitung an der Stelle .
Existiert die Ableitung für alle Werte des Definitionsbereichs?
Nicht jede Funktion besitzt in jedem Punkt eine Ableitung. Das kann zum Beispiel daran liegen, dass die Funktion an einer Stelle einen Knick besitzt oder unstetig ist. So ist zum Beispiel die Betragsfunktion an der Stelle 0 nicht differenzierbar. Der Artikel „Differenzierbarkeit“ liefert zu diesem Thema genauere Informationen.


Die Ableitung als Funktion
Von der Ableitung an einem bestimmten Punkt ist es nur ein kleiner Schritt zur Ableitung auf dem ganzen Definitionsbereich. Denn alle "normalen" Funktionen (die in der Schule behandelt werden) besitzen für alle den gleichen Differenzenquotienten in Abhängigkeit von . In dem Fall kann man die Ableitungen mithilfe der Ableitungsregeln bestimmen.
Höhere Ableitungen
Wenn die erste Ableitung nochmal abgeleitet wird, wird das Ergebnis zweite Ableitung genannt. Die Ableitung der zweiten Ableitung heißt dritte Ableitung und so weiter. Zumeist werden für die Kurvendiskussion nur die ersten drei Ableitungen benötigt.
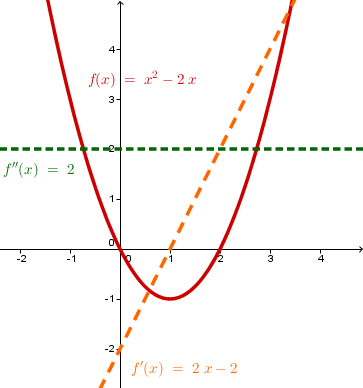
Im Bild erkennt man auch wieder, dass die Ableitung die Steigung der Funktion ist:
Die Ableitung von ist negativ bis 1, und danach positiv. Dementsprechend fällt bis und steigt danach.
Des Weiteren ist eine Gerade mit konstanter Steigung und ist konstant.
Notation
Die Ableitung einer Funktion wird mit einem Strich ( ) nach der Bezeichnung der Funktion gekennzeichnet. Bei höheren Ableitungen fügt man weitere Striche hinzu. Der Übersichtlichkeit halber verwendet man ab der vierten Ableitung statt der jeweiligen Anzahl an Strichen die entsprechende Zahl hochgestellt und eingeklammert.
Funktion
1. Ableitung
2. Ableitung
n-te Ableitung
Wofür braucht man Ableitungen?
Die erste Ableitung gibt die Steigung einer Funktion an.
Hat man eine Funktion gegeben, dann kann man aus der Ableitung zum Beispiel ablesen, wann die Funktion am stärksten steigt bzw. gar nicht steigt und kann dadurch Rückschlüsse ziehen, wie der Funktionsgraph aussieht. Diese Methode dient unter anderem der Bestimmung von Extremstellen bzw. Extremwerten.
Bildet man die Ableitung der Ableitung, so erhält man die zweite Ableitung, sozusagen die Steigung der Steigung. Die zweite Ableitung ist die Krümmung des Funktionsgraphen.
Die zweite Ableitung ermöglicht z.B. eine Antwort auf die Frage: Wann ist die Steigung konstant?
Ableitungen in der Kurvendiskussion
Beispiel | Bedeutung | |
|---|---|---|
Ausgangsfunktion | ||
Erste Ableitung | Steigung von | |
Zweite Ableitung | Krümmung von |
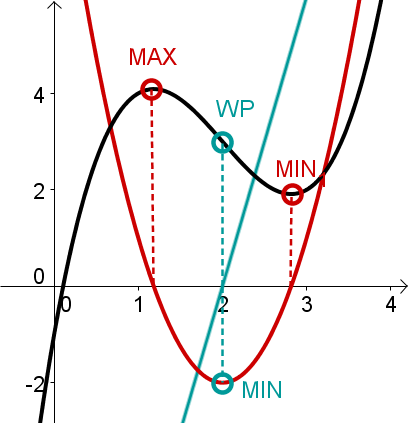
Jeder x-Wert eines Extremums der Funktion ist eine Nullstelle der Ableitung.
Jeder x-Wert eines Wendepunktes einer Funktion ist ein x-Wert eines Extremums der Ableitung.
Jeder x-Wert eines Wendepunktes einer Funktion ist eine Nullstelle der zweiten Ableitung.
Achtung: Die Rückrichtung dieser Aussagen muss nicht richtig sein.
Ableitung und Integral
Das Integral ist das Gegenstück zur Ableitung. Leitet man eine integrierte Funktion ab, erhält man die ursprüngliche Funktion und ebenso umgekehrt (abgesehen von einer Konstante, die hier noch hinzukommen kann). Dieser Zusammenhang ist die Aussage des Hauptsatzes der Differential- und Integralrechnung (HDI).
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum graphischen Differenzieren
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
