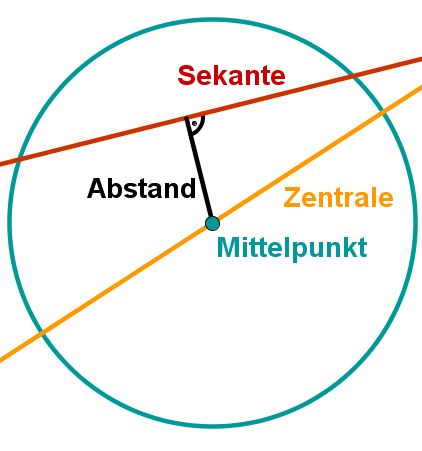
Eine Sekante ist eine Gerade, die eine Kurve in zwei verschiedenen Punkten schneidet.
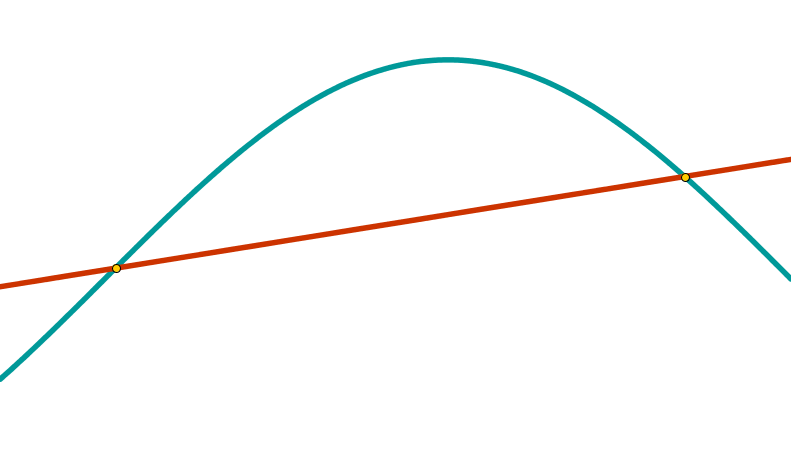
Kreissekante
Sekantensatz
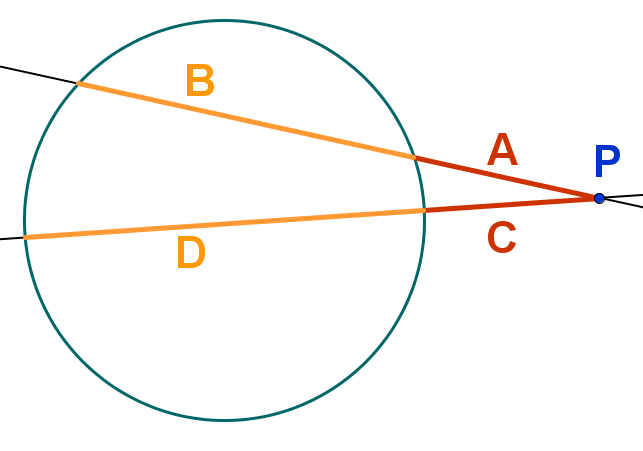
Angenommen, zwei Sekanten schneiden sich außerhalb des Kreises in einem Punkt P.
Dann ist das Größenverhältnis der beiden Strecken von P bis zum Kreis das gleiche wie das Verhältnis der beiden Gesamtstrecken
Im Bild:
Sekanten-Tangenten-Satz
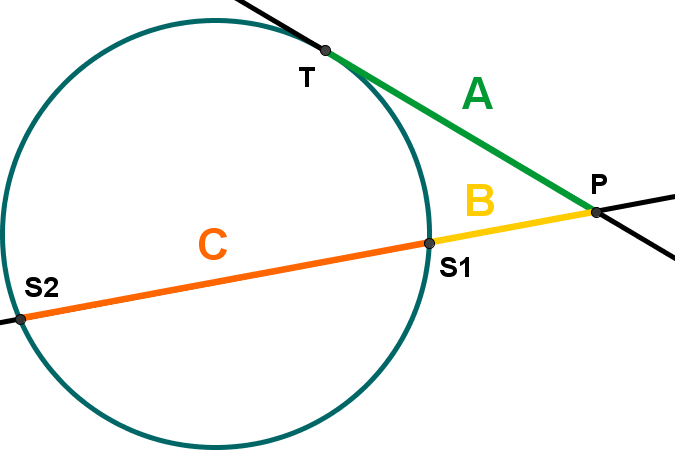
Gegeben sind ein Kreis sowie eine Tangente und eine Sekante, die sich außerhalb des Kreises in einem Punkt P schneiden.
T sei der Berührpunkt der Tangente mit dem Kreis und S1 und S2 die beiden Schnittpunkte der Sekante mit dem Kreis (wobei S1 näher bei P liegt).
Dann verhält sich der Abstand von P und S1 zum Abstand von P und T genauso wie der Abstand von P und T zum Abstand von P und S2.
Im Bild:
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: