Tangente an Kreis

Eine Kreistangente ist eine Gerade, die den Kreis nur in einem Punkt, dem Berührpunkt, berührt. Eine Tangente schneidet im Gegensatz zu einer Sekante den Kreis nicht.

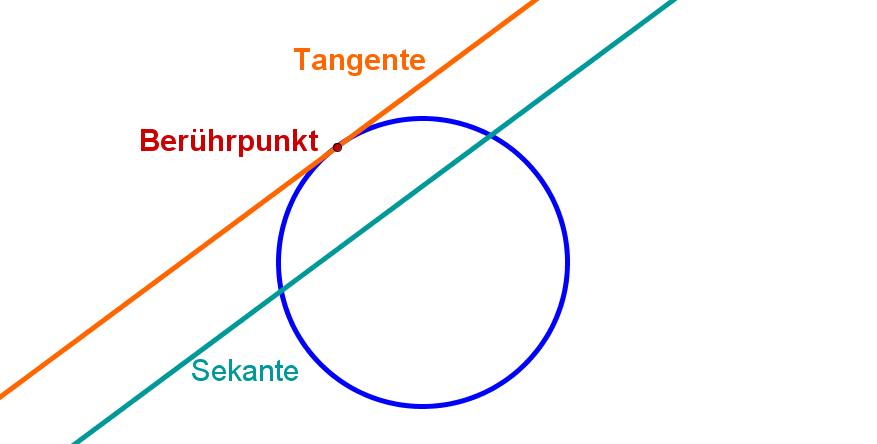
Die Kreistangente $t$ berührt den Kreis im Berührpunkt $B$ . Die Tangente steht immer senkrecht auf dem Radius des Kreises:

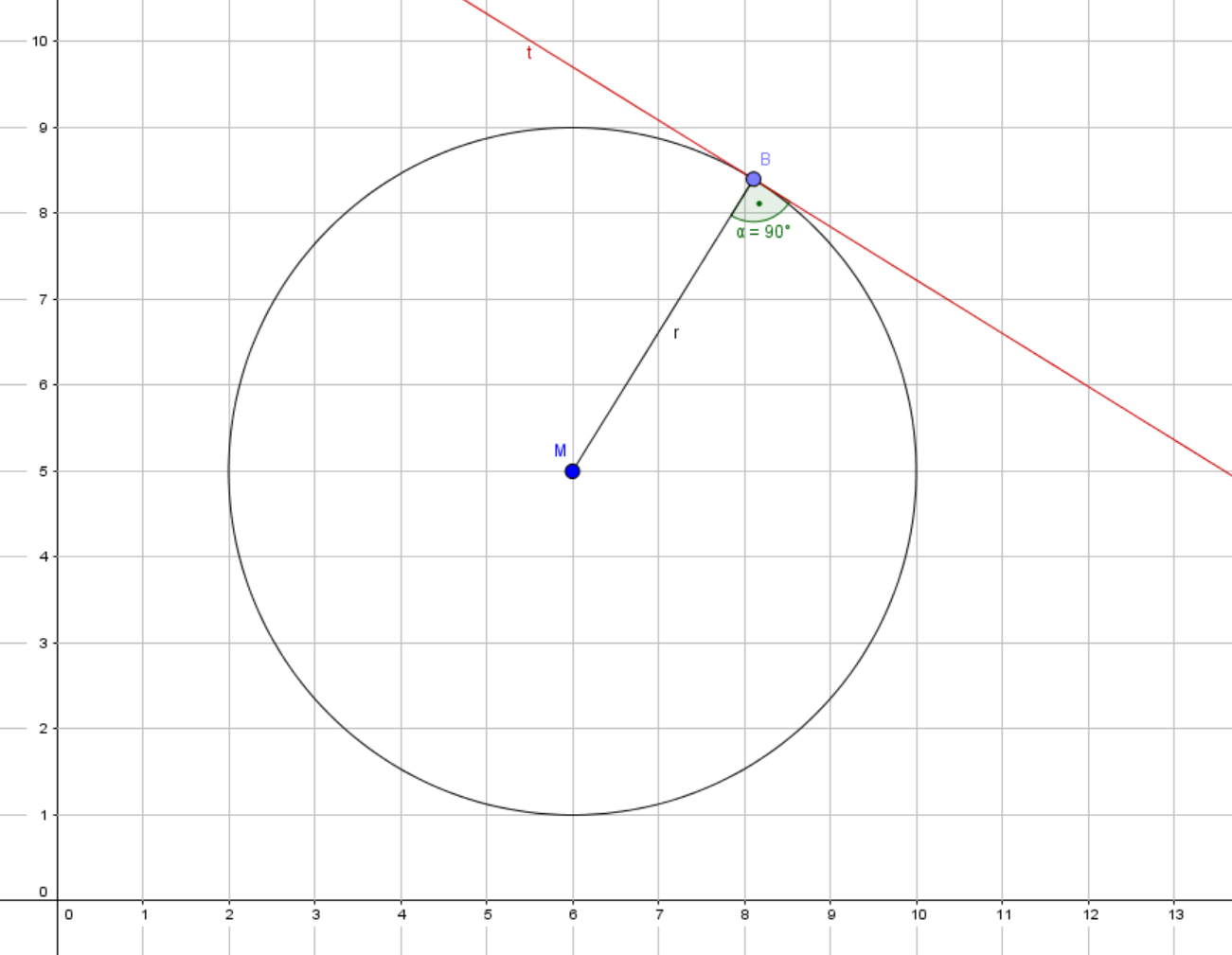
Tangente steht immer senkrecht auf Kreis

Tangente an Kreis berechnen

Wir wollen die Tangentengleichung an einen Kreis durch einen Punkt berechnen. Gegeben ist der Mittelpunkt des Kreises und ein weiterer Punkt. Wir unterscheiden zwei Fälle:

Der gegebene Punkt liegt auf dem Kreis. Der Punkt ist also der Berührpunkt der Tangente mit dem Kreis.
Der gegebene Punkt liegt außerhalb des Kreises. Die Tangente soll durch diesen Punkt verlaufen und zugleich den Kreis berühren.

Der gegebene Punkt liegt auf dem Kreis

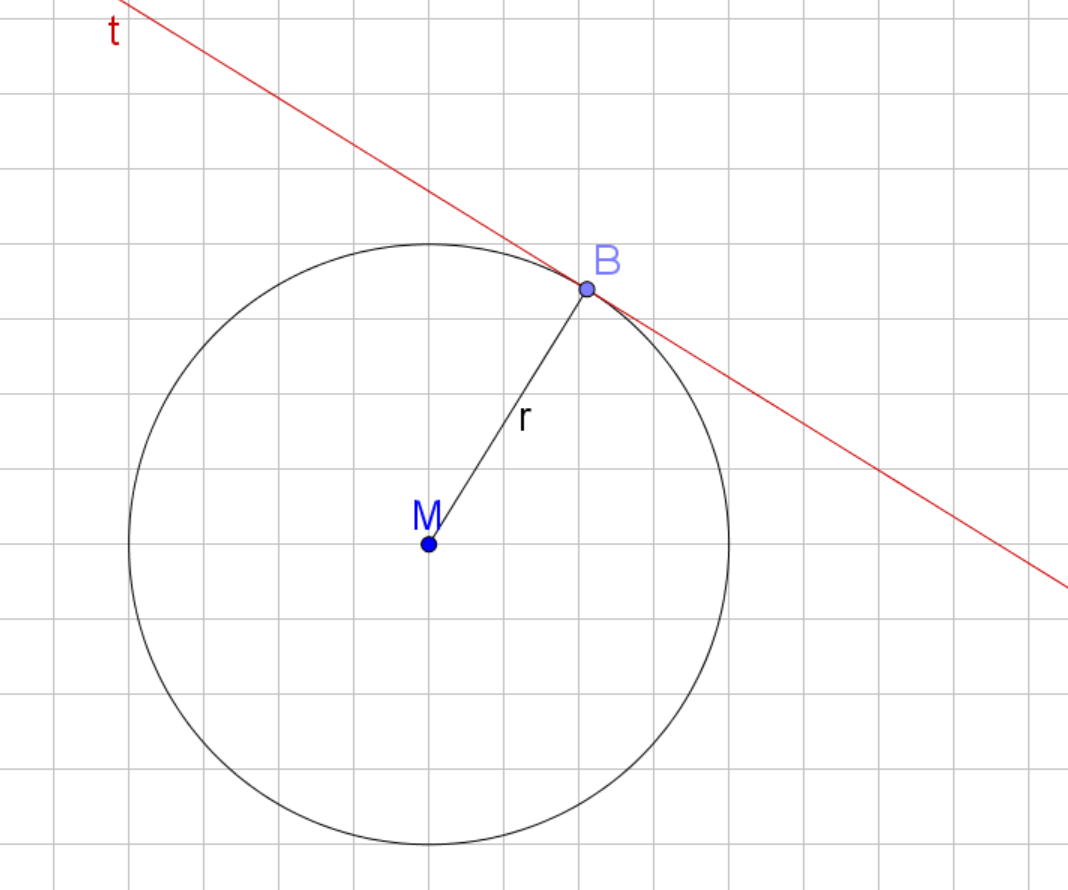
Berührpunkt einer Tangente an einen Kreis

Gegeben ist der Mittelpunkt $M (x_{M}, y_{M})$ sowie der Berührpunkt $B (x_{B}, y_{B})$ . Die Tangentengleichung kannst du mit diesen Schritten bestimmen:

Berechne die Steigung $m_{g}$ der Geraden, die durch $M$ und $B$ verläuft.
Die Steigung $m_{t}$ der Tangente erhältst du durch $m_{t} = - \frac{1}{m_{g}}$ , weil für senkrechte Geraden das Produkt ihrer Steigungen immer $- 1$ ergibt.
Setze den Punkt $B$ in die Tangentengleichung $t (x) = m_{t} \cdot x + k$ ein und löse nach $k$ auf.
Jetzt kannst du $m_{t}$ und $k$ in die Tangentengleichung einsetzen.

Beispiel:

Bestimme die Gleichung der Tangente, die den Kreis mit dem Mittelpunkt $M (3 | 1)$ im Punkt $P (6 | 3,65)$ berührt.

Wir berechnen die Steigung der Geraden $g$ , die durch $M$ und $P$ verläuft. Dafür machen wir uns das Steigungsdreieck zunutze:

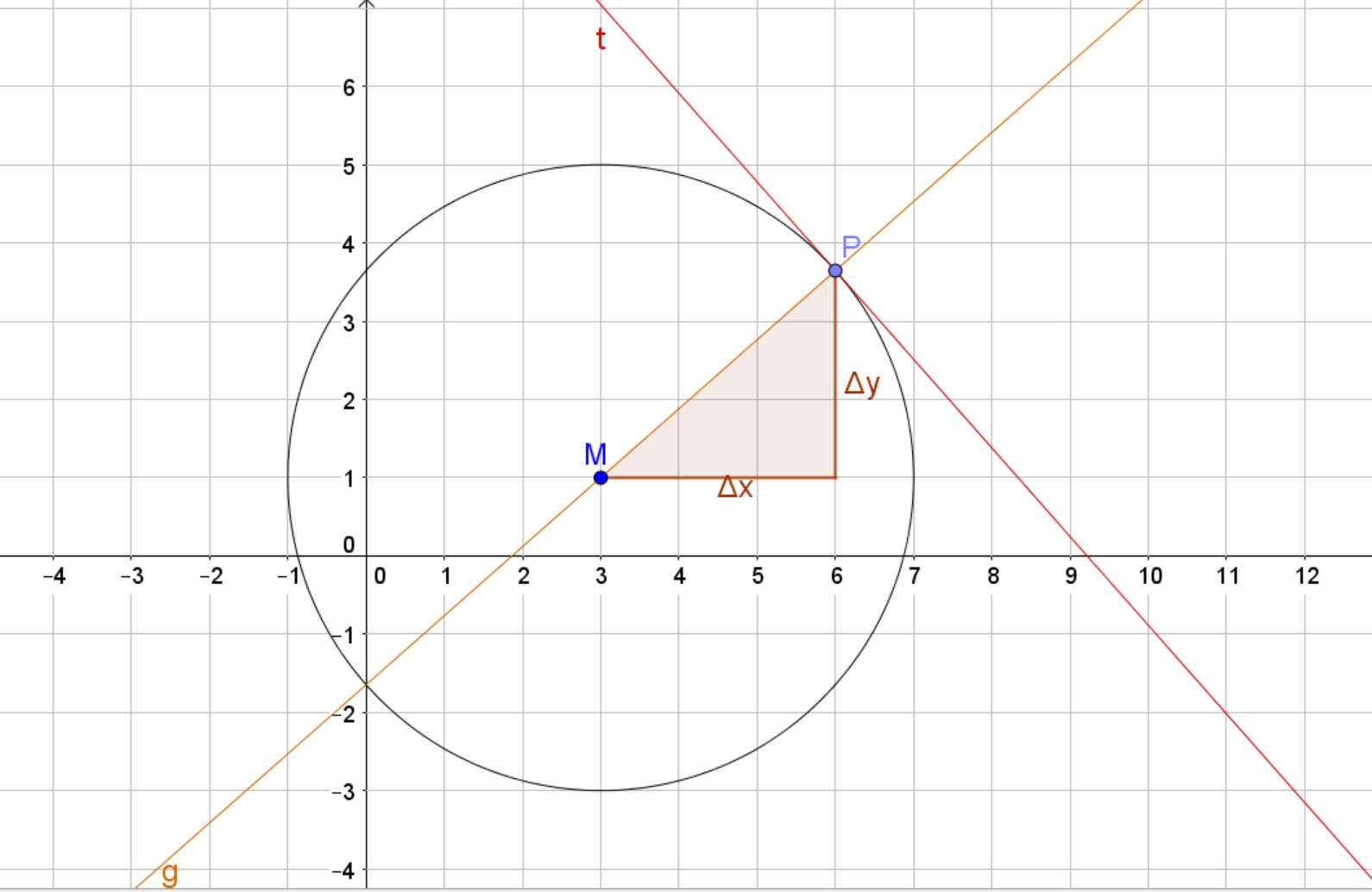
Steigungsdreieck der Geraden, die durch Mittelpunkt und Berührpunkt verläuft

Die Steigung $m_{g}$ der Geraden $g$ ist demnach die Differenz der $y$ -Koordinaten von $P$ und $M$ geteilt durch die Differenz ihrer $x$ -Koordinaten:

m_{g} = \frac{Δ y}{Δ x} = \frac{y_{P} - y_{M}}{x_{P} - x_{M}} = \frac{3,65 - 1}{6 - 3} = \frac{2,65}{3} \approx 0,883

Die Tangente $t$ steht senkrecht auf dieser Geraden $g$ . Für senkrechte Geraden ergibt das Produkt ihrer Steigungen immer $- 1$ :

m_{g} \cdot m_{t} = - 1

Wenn wir durch $m_{g}$ teilen, erhalten wir die Formel für die Steigung der Tangente:

m_{t} = - \frac{1}{m_{g}} = - \frac{1}{0,883} \approx - 1,13

Nun haben wir bereits die Steigung der Tangente berechnet. Für die Tangentengleichung $t (x) = m_{t} \cdot x + k_{t}$ müssen wir also jetzt noch den $y$ -Achsenabschnitt $k_{t}$ der Tangente berechnen. Hierfür setzen wir den Punkt $P$ , der auf der Tangente liegt, in die Tangentengleichung ein und lösen nach $k_{t}$ auf:

$t (x)$	$=$	$- 1,13 x + k_{t}$
	↓	Setze $P$ in die Gleichung ein
$3,65$	$=$	$- 1,13 \cdot 6 + k_{t}$
	↓	Ausrechnen
$3,65$	$=$	$- 6,78 + k_{t}$	$+ 6,78$
$10,43$	$=$	$k_{t}$

Der $y$ -Achsenabschnitt der Tangente ist also $k_{t} = 10,43$ .

Damit haben wir alles ausgerechnet und müssen nun nur noch die vollständige Tangentengleichung notieren:

$t (x) = - 1,13 x + 10,43$

Der gegebene Punkt liegt außerhalb des Kreises

Gegeben ist der Mittelpunkt $M (x_{M}, y_{M})$ und der Radius $r$ des Kreises sowie ein Punkt $Q (x_{Q}, y_{Q})$ außerhalb des Kreises. Graphisch können wir erkennen, dass es zwei Kreistangenten gibt, die durch den Punkt $Q$ verlaufen.

zwei Tangenten an einen Kreis durch einen Punkt außerhalb des Kreises

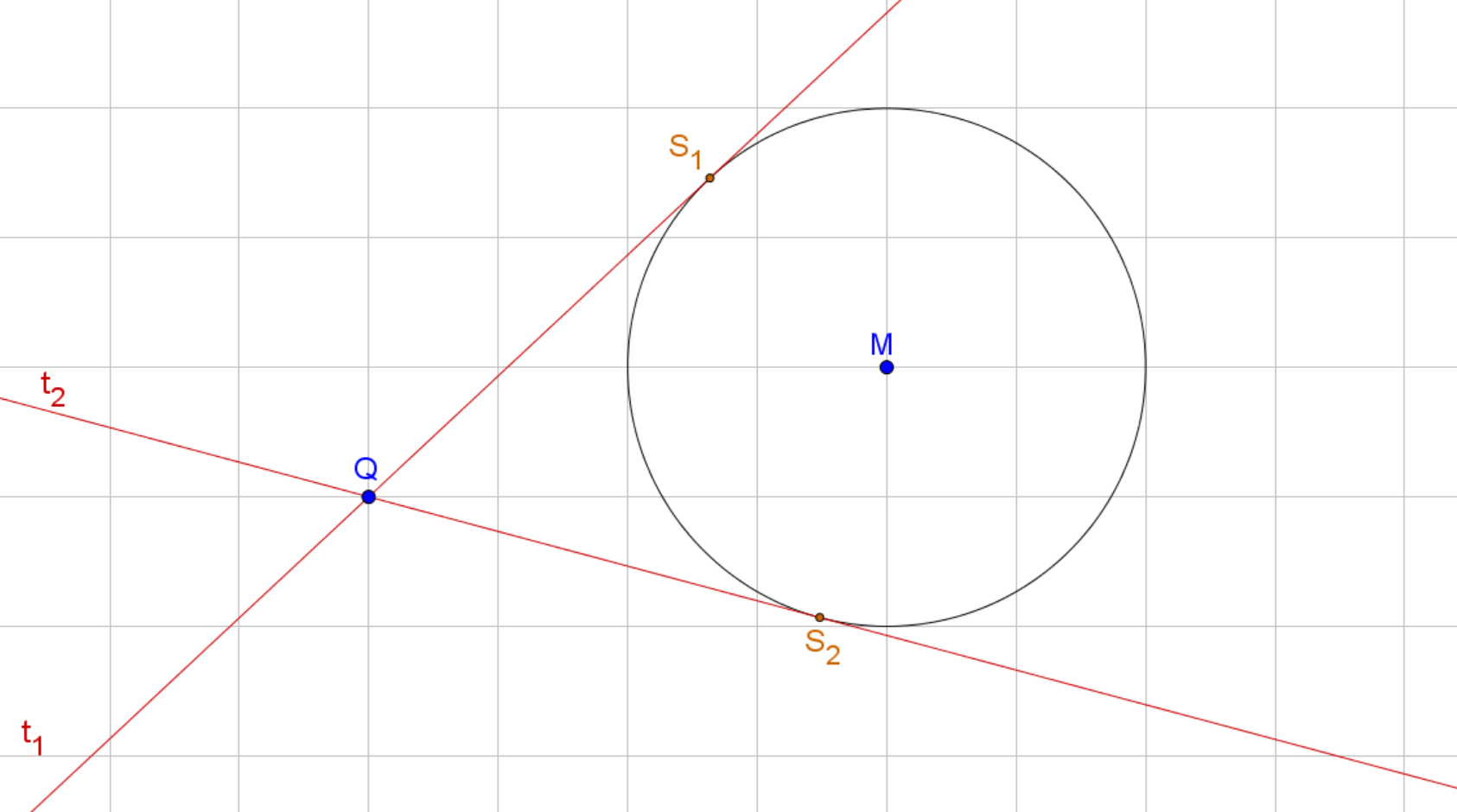
Wir wissen, dass die Tangente senkrecht auf dem Radius des Kreises steht. Deshalb können wir sowohl für $S_{1}$ und $S_{2}$ ein rechtwinkliges Dreieck konstruieren.

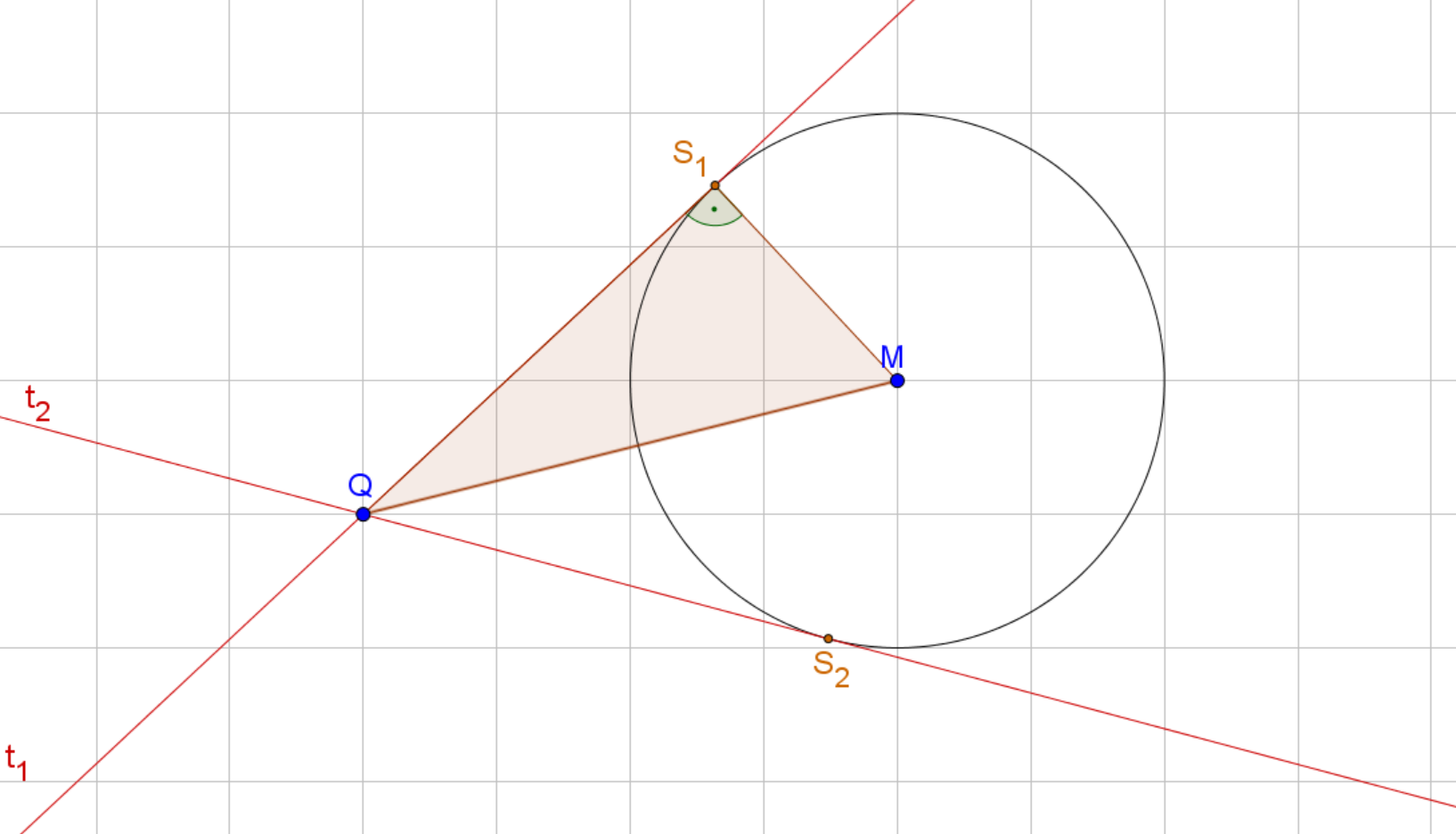
rechtwinkliges Dreieck durch Mittelpunkt, Punkt außerhalb des Kreises und Berührpunkt. Rechter Winkel liegt im Berührpunkt

Dieses rechtwinklige Dreieck besitzt seinen rechten Winkel immer im Berührpunkt $S_{1}$ mit dem Kreis. Deshalb können wir über die Strecke $Q M$ einen Thaleskreis legen. $S_{1}$ liegt auf diesem Thaleskreis. Deshalb hat das Dreieck mit der Hypotenuse $Q M$ in $S_{1}$ einen rechten Winkel.

Der Mittelpunkt $T$ dieses Thaleskreises liegt genau auf der Hälfte der Strecke $Q M$ .

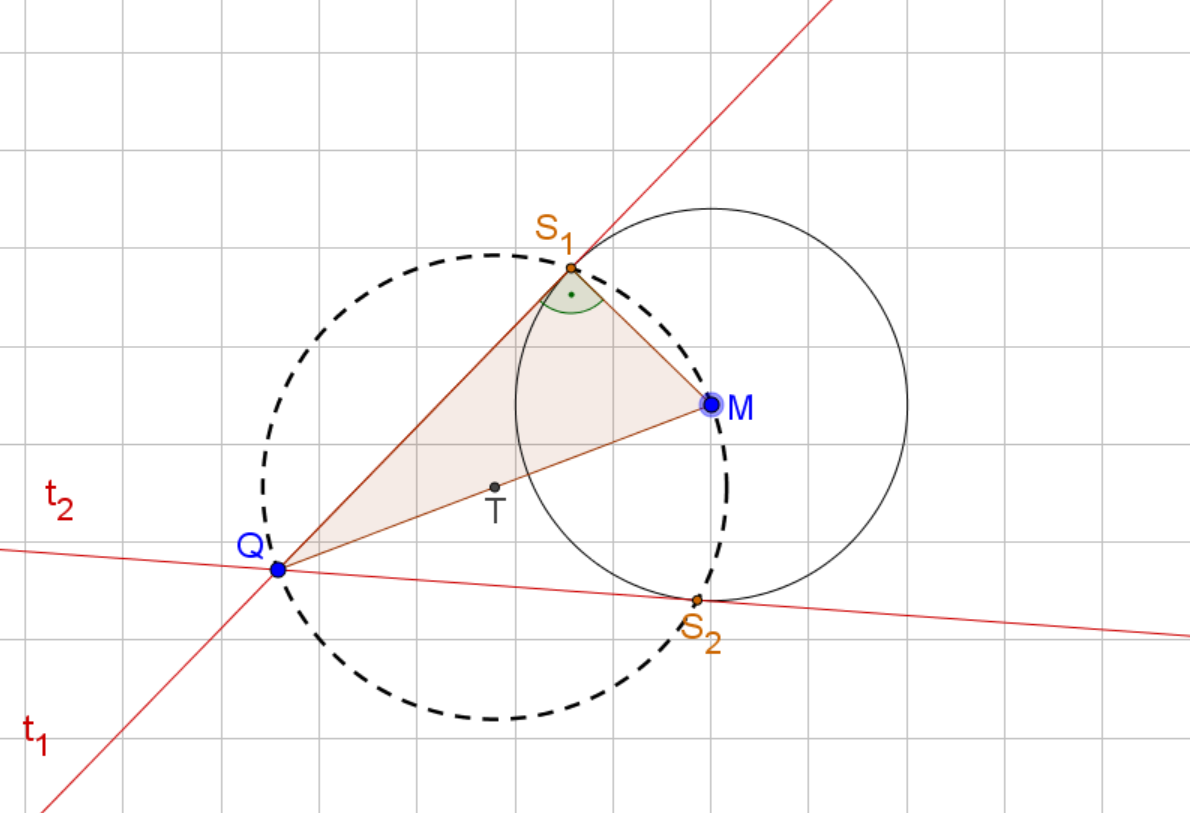
Thaleskreis, wobei die Strecke vom Mittelpunkt des ursprünglichen Kreises zum Punkt außerhalb des Kreises den Durchmesser bilden

Um die Tangenten durch $Q$ an den Kreis zu berechnen, kannst du die folgenden Schritte befolgen:

Stelle die Kreisgleichung für den Kreis $k_{1}$ mit Mittelpunkt $M$ auf:

k_{1} : (x - x_{M})^{2} + (y - y_{M})^{2} = r^{2}

Berechne die Koordinaten des Mittelpunktes $T$ des Thaleskreises. Dieser befindet sich genau in der Mitte der Strecke $Q M$ . Deshalb sind die Koordinaten von $T$ die "durchschnittlichen" $x$ - bzw. $y$ -Koordinaten von $Q$ und $M$ . $T (\frac{1}{2} (x_{M} + x_{Q}); \frac{1}{2} (y_{M} + y_{Q}))$

Stelle die Kreisgleichung für den Thaleskreis $k_{2}$ mit Mittelpunkt $T$ auf:

k_{2} : (x - x_{T})^{2} + (y - y_{T})^{2} = {(\frac{Q M}{2})}^{2}

Berechne die Schnittpunkte der beiden Kreise. Das entspricht $S_{1}$ und $S_{2}$ , also den Berührpunkten der Tangenten an $k_{1}$ . Du kannst die Schnittpunkte berechnen, indem du eine der beiden Gleichungen nach $x$ oder $y$ auflöst und dann in die andere Gleichung einsetzt. Du erhältst dann sowohl für $x$ , als auch für $y$ zwei Lösungen, die den beiden Punkten $S_{1}$ und $S_{2}$ entsprechen.

Wenn du $S_{1}$ und $S_{2}$ berechnet hast, hast du die beiden Berührpunkte der Tangenten an den Kreis. Du hast das kompliziertere Problem dann auf das obige Problem zurückgeführt: Nämlich wie man eine Tangente an den Kreis berechnet, wenn der gegebene Punkt auf dem Kreis liegt. Du kannst dann vorgehen, wie oben beschreiben.

Anmerkung: Die hier beschriebene Rechnung kann sich als sehr kompliziert und langwierig erweisen. Meistens wird die Rechnung in der Schule nicht gefordert.

Tangente an Kreis berechnen mit Vektoren

Der gegebene Punkt liegt auf dem Kreis

Wenn du bereits mit Vektoren und vektoriell dargestellten Geradengleichungen umgehen kannst, findest du hier eine alternative Lösungsmethode zu der oben dargestellten.

Gegeben ist der Mittelpunkt $\vec{M} = (\begin{array}{c} M_{x} \\ M_{y} \end{array})$ und der Berührpunkt der Tangente an den Kreis $\vec{B} = (\begin{array}{c} B_{x} \\ B_{y} \end{array})$ .

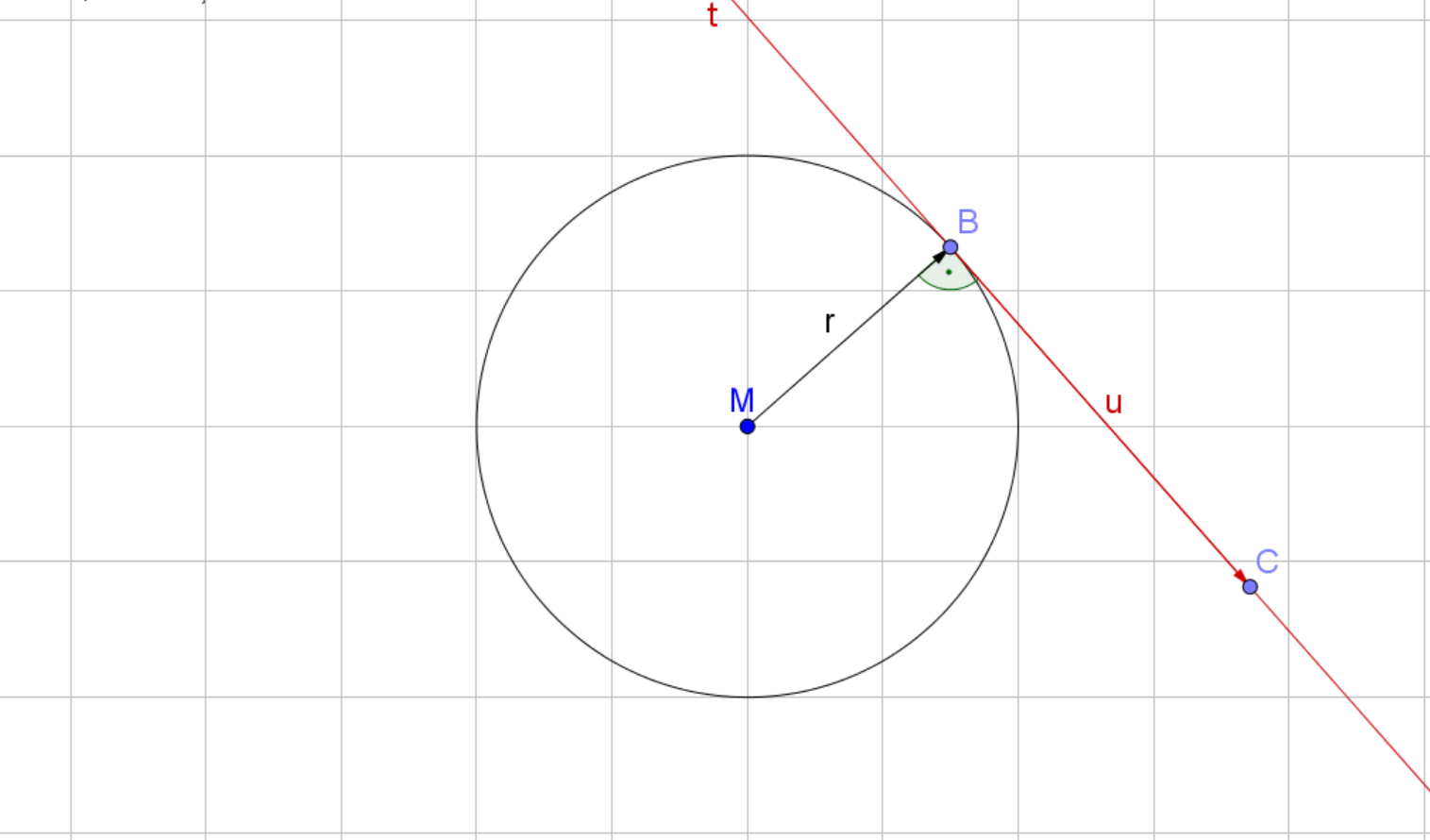
Kreis mit Berührpunkt und Richtungsvektor der Tangente

Die Tangentengleichung $t$ kannst du mit diesen Schritten bestimmen:

Berechne den Radiusvektor $\vec{r} = \vec{B} - \vec{M}$
Finde einen Vektor $\vec{u}$ , der senkrecht auf $\vec{r}$ steht. Dafür gilt $\vec{r} \cdot \vec{u} = 0$ . $\vec{u}$ ist der Richtungsvektor der Tangente.
$\vec{B}$ ist der Aufpunkt der Tangente. Du kannst nun die Tangentengleichung formulieren: $t : \vec{X} = \vec{u} \cdot λ + \vec{B}$

Beispiel:

Stelle die Gleichung der Tangente auf, die den Kreis mit Mittelpunkt $\vec{M} = (\begin{array}{c} 16 \\ 8 \end{array})$ im Punkt $\vec{B} = (\begin{array}{c} 19 \\ 10,65 \end{array})$ berührt.

$\vec{r} = \vec{B} - \vec{M} = (\begin{array}{c} 19 \\ 10,65 \end{array}) - (\begin{array}{c} 16 \\ 8 \end{array}) = (\begin{array}{c} 3 \\ 2,65 \end{array})$

Wir suchen nun einen Vektor $\vec{u} = (\begin{array}{c} u_{x} \\ u_{y} \end{array})$ , für den das Skalarprodukt mit $\vec{r}$ Null ergibt. Hierfür kannst du immer den Vektor $\vec{u} = (\begin{array}{c} - r_{y} \\ r_{x} \end{array})$ nehmen, weil:

(- r_{y}) \cdot r_{x} + r_{x} \cdot r_{y}

=

0

Der Richtungsvektor der Tangente ist daher:

$\vec{u} = (\begin{array}{c} - 2,65 \\ 3 \end{array})$

Der Punkt $\vec{B} = (\begin{array}{c} 19 \\ 10,65 \end{array})$ liegt auf der Tangente und kann somit als Aufpunkt verwendet werden. Die Tangentengleichung lautet dann:

$t : \vec{X} = (\begin{array}{c} 19 \\ 10,65 \end{array}) + λ \cdot (\begin{array}{c} - 2,65 \\ 3 \end{array})$

Der gegebene Punkt liegt außerhalb des Kreises

Vor allem, wenn der gegebene Punkt außerhalb des Kreises liegt, vereinfacht die Vektorrechnung die Berechnung der Tangente sehr.

Gegeben ist der Mittelpunkt $\vec{M} = (\begin{array}{c} M_{x} \\ M_{y} \end{array})$ und der Radius $r$ des Kreises sowie ein Punkt $\vec{Q} = (\begin{array}{c} Q_{x} \\ Q_{y} \end{array})$ außerhalb des Kreises.

Wir wollen die beiden Tangenten berechnen, die durch $\vec{Q}$ verlaufen und den Kreis in den Punkten $\vec{S_{1}}$ und $\vec{S_{2}}$ berühren.

zwei Tangenten an einen Kries durch einen Punkt außerhalb des Kreises

Die beiden Schnittpunkte $\vec{S_{1}}$ und $\vec{S_{2}}$ kannst du mit dieser Formel berechnen:

$\begin{array}{l} \vec{S} = \vec{M} + \frac{r^{2}}{∣ \vec{M Q} ∣^{2}} \cdot (\begin{array}{c} Q_{x} - M_{x} \\ Q_{y} - M_{y} \end{array}) \pm \sqrt{r^{2} - {(\frac{r^{2}}{∣ \vec{M Q} ∣})}^{2}} \cdot \frac{1}{∣ \vec{M Q} ∣} \cdot (\begin{array}{c} - Q_{y} + M_{y} \\ Q_{x} - M_{x} \end{array}) \\ = \vec{M} + \frac{r^{2}}{∣ \vec{M Q} ∣^{2}} \cdot (\begin{array}{c} Q_{x} - M_{x} \\ Q_{y} - M_{y} \end{array}) \pm \sqrt{∣ \vec{M Q} ∣^{2} - r^{2}} \cdot \frac{r}{∣ \vec{M Q} ∣^{2}} \cdot (\begin{array}{c} - Q_{y} + M_{y} \\ Q_{x} - M_{x} \end{array}) \end{array}$

Die beiden verschiedenen Punkte $\vec{S_{1}}$ und $\vec{S_{2}}$ ergeben sich dadurch, indem du einmal für das $\pm$ ein $+$ einsetzt und das andere Mal ein $-$ .

Um jeweils die Tangentengleichung durch $\vec{S_{1}}$ und $\vec{S_{2}}$ zu berechnen, kannst du so vorgehen wie im obigen Abschnitt, da wir ja nun den Berührpunkt der Tangente mit dem Kreis gegeben haben.

Beispiel:

Berechne die Tangenten, die durch den Punkt $Q = (- 2 | 4)$ außerhalb des Kreises mit Mittelpunkt $M = (5 | 5)$ und Radius $r = 2$ verlaufen.

Berechnung der Berührpunkte der Tangenten mit dem Kreis

Mit der oberen Formel können wir die beiden Berührpunkte $\vec{S_{1}}$ und $\vec{S_{2}}$ berechnen. Davor berechnen wir $∣ \vec{M Q} ∣$ , um die Rechnung mit der Formel etwas übersichtlicher zu gestalten:

$∣ \vec{M Q} ∣ = ∣ \vec{Q} - \vec{M} ∣ = | (\begin{array}{c} - 2 \\ 4 \end{array}) - (\begin{array}{c} 5 \\ 5 \end{array}) | = | (\begin{array}{c} - 7 \\ - 1 \end{array}) | = \sqrt{(- 7)^{2} + (- 1)^{2}} = \sqrt{50}$

$\vec{S} = (\begin{array}{c} 5 \\ 5 \end{array}) + \frac{2^{2}}{{\sqrt{50}}^{2}} \cdot (\begin{array}{c} - 2 - 5 \\ 4 - 5 \end{array}) \pm \sqrt{50 - 4} \cdot \frac{2}{50} \cdot (\begin{array}{c} - 4 + 5 \\ - 2 - 5 \end{array})$

Jetzt rechnen wir aus:

$\vec{S} = (\begin{array}{c} 5 \\ 5 \end{array}) + \frac{4}{50} \cdot (\begin{array}{c} - 7 \\ - 1 \end{array}) \pm \sqrt{46} \cdot \frac{1}{25} \cdot (\begin{array}{c} 1 \\ - 7 \end{array})$

$\vec{S} = (\begin{array}{c} 5 \\ 5 \end{array}) + (\begin{array}{c} - \frac{14}{25} \\ - \frac{4}{50} \end{array}) \pm \frac{\sqrt{46}}{25} \cdot (\begin{array}{c} 1 \\ - 7 \end{array})$

$\vec{S} = \frac{1}{25} (\begin{array}{c} 111 \\ 123 \end{array}) \pm \frac{\sqrt{46}}{25} (\begin{array}{c} 1 \\ - 7 \end{array})$

Ein Berührpunkt der Tangente an den Kreis ist also:

$\vec{S_{1}} = \frac{1}{25} (\begin{array}{c} 111 + \sqrt{46} \\ 123 - 7 \sqrt{46} \end{array}) \approx (\begin{array}{c} 4,71 \\ 3,02 \end{array})$

und der zweite Berührpunkt ist:

$\vec{S_{2}} = \frac{1}{25} (\begin{array}{c} 111 - \sqrt{46} \\ 123 + 7 \sqrt{46} \end{array}) \approx (\begin{array}{c} 4,17 \\ 6,82 \end{array})$

Berechnung der Tangentengleichung für $\vec{S_{1}}$

Nach dem oben beschriebenen Vorgehen berechnen wir nun die Tangentengleichung für die Tangente, die den Kreis im Punkt $\vec{S_{1}}$ berührt.

Dafür berechnen wir als erstes den Radiusvektor $\vec{r_{1}}$ :

$\vec{r_{1}} = \vec{S_{1}} - \vec{M} = (\begin{array}{c} 4,71 \\ 3,02 \end{array}) - (\begin{array}{c} 5 \\ 5 \end{array}) = (\begin{array}{c} - 0,29 \\ - 1,98 \end{array})$

Als Nächstes berechnen wir den Richtungsvektor $\vec{u_{1}}$ der Tangente. Dieser steht senkrecht auf $\vec{r_{1}}$ , d.h. $\vec{r_{1}} \cdot \vec{u_{1}} = 0$ .

$\vec{u_{1}} = (\begin{array}{c} - r_{y} \\ r_{x} \end{array}) = (\begin{array}{c} 1,98 \\ - 0,29 \end{array})$

Nun können wir die Tangentengleichung aufschreiben, weil wir den Richtungsvektor $\vec{u_{1}}$ berechnet haben und einen Punkt haben, der auf der Tangente liegt, nämlich $\vec{S_{1}}$ :

$t_{1} : \vec{X} = \vec{S_{1}} + λ \cdot \vec{u_{1}} = (\begin{array}{c} 4,71 \\ 3,02 \end{array}) + λ \cdot (\begin{array}{c} 1,98 \\ - 0,29 \end{array})$

Berechnung der Tangentengleichung für $\vec{S_{2}}$

$\vec{r_{2}} = \vec{S_{2}} - \vec{M} = (\begin{array}{c} 4,17 \\ 6,82 \end{array}) - (\begin{array}{c} 5 \\ 5 \end{array}) = (\begin{array}{c} - 0,83 \\ 1,82 \end{array})$

$\vec{u_{2}} = (\begin{array}{c} - r_{y} \\ r_{x} \end{array}) = (\begin{array}{c} - 1,82 \\ - 0,83 \end{array})$

$t_{2} : \vec{X} = \vec{S_{2}} + λ \cdot \vec{u_{2}} = (\begin{array}{c} 4,17 \\ 6,82 \end{array}) + λ \cdot (\begin{array}{c} - 1,82 \\ - 0,83 \end{array})$

Wir können alternativ als Richtungsvektoren natürlich auch $\vec{Q S_{1}}$ bzw. $\vec{Q S_{2}}$ verwenden.

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

Tangente an Kreis

Tangente an Kreis berechnen

Der gegebene Punkt liegt auf dem Kreis

Beispiel:

Der gegebene Punkt liegt außerhalb des Kreises

Tangente an Kreis berechnen mit Vektoren

Der gegebene Punkt liegt auf dem Kreis

Beispiel:

Der gegebene Punkt liegt außerhalb des Kreises

Beispiel:

Berechnung der Berührpunkte der Tangenten mit dem Kreis

Berechnung der Tangentengleichung für S1→

Berechnung der Tangentengleichung für S2→

Du hast noch nicht genug vom Thema?

Artikel

Berechnung der Tangentengleichung für $\vec{S_{1}}$

Berechnung der Tangentengleichung für $\vec{S_{2}}$