Die Steigung einer Funktion (auch genannt Anstieg) ist ein Maß dafür, wie steil der Graph einer Funktion ansteigt oder abfällt.

Mathematisch lässt sich die Steigung beschreiben als das Verhältnis von der Abweichung in -Richtung zu der Abweichung in -Richtung.
Aus der Steigung erhält man den Steigungswinkel mithilfe des Tangens über die Beziehung:
Steigung berechnen
Bei Geraden
In einer allgemeinen Geradengleichung wird die Steigung meist genannt.
Sie lässt sich mithilfe von zwei Punkten und dem Differenzenquotienten berechnen:
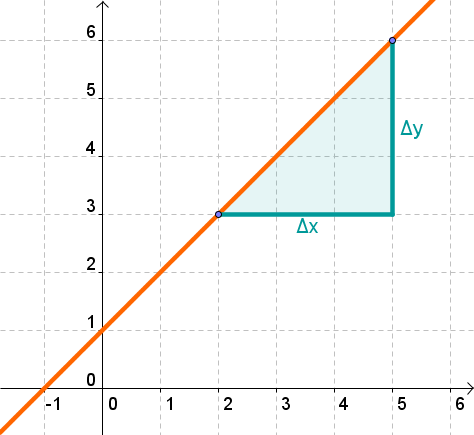
Weiterführende Informationen und Beispielaufgaben sind in dem Artikel Geradensteigung.
Bei Graphen in einem bestimmten Punkt
Steigungswinkel
Der Steigungswinkel gibt an, in welchem Winkel eine Gerade zur -Achse steht.
Statt vom Steigungswinkel spricht man oft auch vom Neigungswinkel der Geraden.

Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu linearen Funktionen und Geradengleichungen
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:

