Differenzenquotient

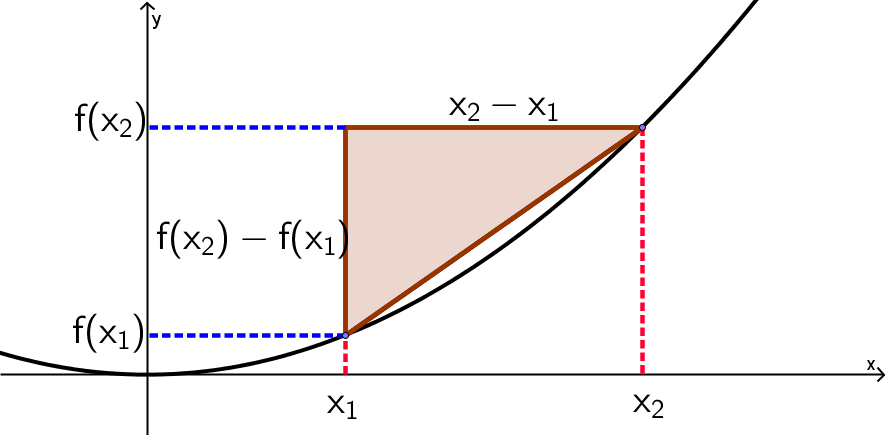
Der Differenzenquotient zwischen zwei Stellen $x_1$ und $x_2$ beschreibt die Steigung der Sekanten zwischen den Punkten $P\left(x_1 \mid f(x_1)\right)$ und $Q\left(x_2 \mid f(x_2)\right)$ :

\displaystyle \frac{f(x_2)-f(x_1)}{x_2-x_1}.

Der Differenzenquotient berechnet die mittlere Änderungsrate. Durch Grenzwertbildung erhält man den Differentialquotienten, mit dessen Hilfe man die Ableitung (= lokale Änderungsrate) berechnen kann.

Beispiel

Bestimme den Differenzenquotienten der Funktion $f(x)=x^2$ im Intervall $\left[1;3\right]$ $\Rightarrow x_1=1$ und $x_2=3$ .

\displaystyle \frac{f(x_2)-f(x_1)}{x_2-x_1}.

Video zum Differenzenquotienten

Laden

Applet

Im folgenden Applet kannst du dir für eine beliebige Funktion $f$ den Differenzenquotienten anschauen und berechnen lassen. Außerdem kannst du die Lage der Stellen $x_1$ und $x_2$ frei wählen.

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/nnrmthf4]

Übungsaufgaben: Differenzenquotient

Laden

Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Differenzen- und Differentialquotient

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Artikel

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?