Eine Gerade ist die unendliche Verlängerung der kürzesten Verbindung zwischen zwei Punkten. Anschaulich ist eine Gerade eine unendlich lange, gerade Linie. Zwischen zwei Punkten gibt es immer genau eine Gerade.
Alle Geraden können durch eine lineare Gleichung dargestellt werden, daher nennt man Geraden auch lineare Funktionen.
Allgemeine Geradengleichung
Um die Gerade aufzustellen, braucht man lediglich die Steigung und den Schnittpunkt der Gerade mit der y-Achse.
Bei dieser Gleichung ist die Steigung der Geraden und der y-Wert, in dem die Gerade die y-Achse schneidet.
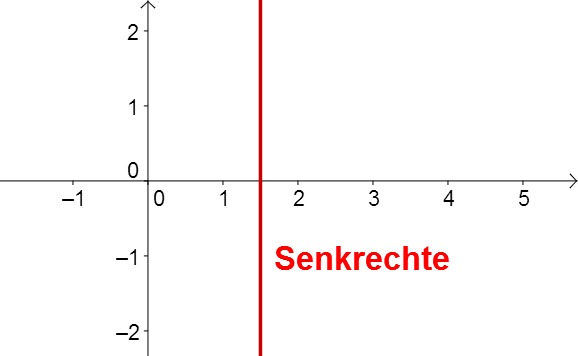
Hier findest du alles über Geraden, die nicht parallel zur -Achse sind.
Über Geraden parallel zu -Achse findest du hier etwas.
Bestandteile der Geradengleichung
Eine Geradengleichung besteht aus einer Steigung und dem y-Achsenabschnitt t. Diese Bestandteile werden im Folgenden näher erläutert.
Als Beispiel betrachten wir die Gerade:
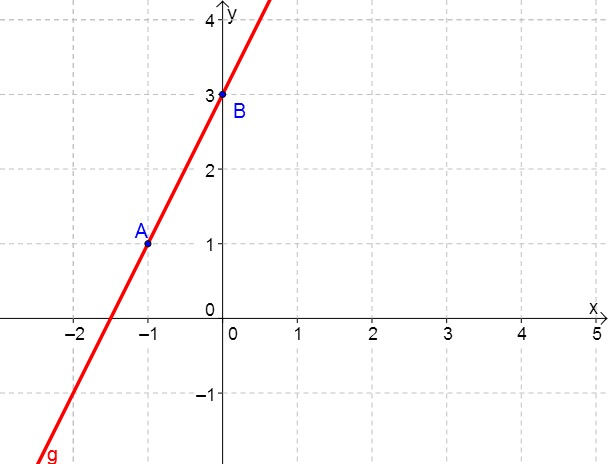
Steigung
Die Steigung gibt an, wie schnell eine Gerade steigt oder fällt. Aus der gegebenen Gleichung kann man hier die Steigung herauslesen.
Wüsste man das nicht, könnte man die Steigung auch anhand eines Steigungsdreiecks bestimmen. Dazu benötigt man mindestens zwei verschiedene Punkte, die man durch Einsetzen verschiedener x-Werte erhalten kann.
Der y-Achsenabschnitt t
Der y-Achsenabschnitt gibt an, in welchem y-Wert die Gerade die y-Achse schneidet. Man erhält den Wert auch, indem man für Null in die Geradengleichung einsetzt, da für den Fall wegfällt und von der ursprünglichen Gleichung nur noch übrig bleibt.
Dass der y-Achsenabschnitt im Beispiel den Wert hat, erkennt man in der Zeichnung auch daran, dass die Gerade die y-Achse im Punkt schneidet. hat die Koordinaten .
Geradengleichung durch zwei verschiedene Punkte berechnen
Beispiel 1: Gegeben sind die Punkte und . Berechne die Gleichung der Geraden, die durch und verläuft.
Berechne die Steigung mit dem Differenzenquotienten
Setze und einen beliebigen Punkt in die Geradengleichung ein, um zu bestimmen. Wir verwenden den Punkt .
Setze und in die allgemeine Geradengleichung ein.
Beispiel 2: Gegeben sind die Punkte und . Berechne die Gleichung der Geraden, die durch und verläuft.
Verwende die Zwei-Punkte-Form der Geradengleichung:
| ↓ | Setze und ein. | ||
| ↓ | Vereinfache. | ||
| ↓ | Löse die Klammer auf. | ||
| ↓ | Fasse zusammen. | ||
Berechne die Geradengleichung, wenn die Steigung und ein Punkt gegeben sind.
Beispiel: Gegeben sind die Steigung und der Punkt . Berechne die zugehörende Geradengleichung.
1. Setze und die Koordinaten des Punktes in die allgemeine Geradengleichung ein und löse nach auf.
2. Setze und in die allgemeine Geradengleichung ein
Berechne die Geradengleichung, wenn der -Achsenabschnitt und ein Punkt gegeben sind.
Beispiel: Gegeben sind der -Achsenabschnitt und der Punkt . Berechne die zugehörende Geradengleichung.
1. Setze und die Koordinaten des Punktes in die allgemeine Geradengleichung ein und löse nach auf.
2. Setze und in die allgemeine Geradengleichung ein
Allgemeine Geraden (interaktiv)
Besondere Geraden
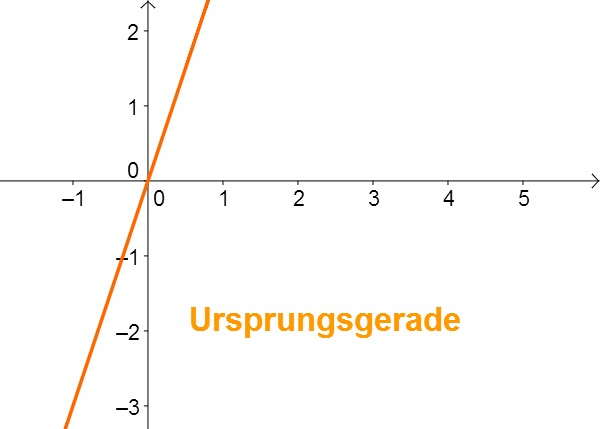
Ursprungsgeraden
Eine Gerade, die durch den Nullpunkt (oder auch Koordinatenursprung) geht, bezeichnet man als Ursprungsgerade. Eine solche Gerade hat immer die Geradengleichung , da gilt.
Eine Ursprungsgerade ist der Funktionsgraph einer direkten Proportionalität.
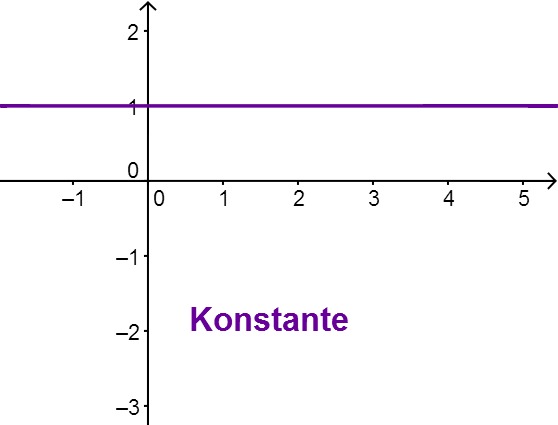
Konstante Funktionen
Eine Gerade, die parallel zur x-Achse verläuft, hat die Form und wird als konstante Funktion bezeichnet, da sie immer den gleichen, konstanten Wert annimmt.
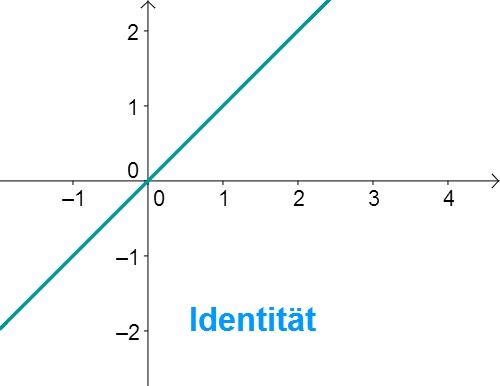
Die Identität
Die Ursprungsgerade mit der Funktion nennt man Identität. Sie ist die Winkelhalbierende des ersten und dritten Quadranten des Koordinatensystems.
Übungsaufgaben
Laden
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Aufstellen der Geradengleichung
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema: