Aufgaben zum Aufstellen der Geradengleichung

Hier findest du Übungsaufgaben zu Geraden. Lerne, Geradengleichungen anhand verschiedener Informationen aufzustellen.

1
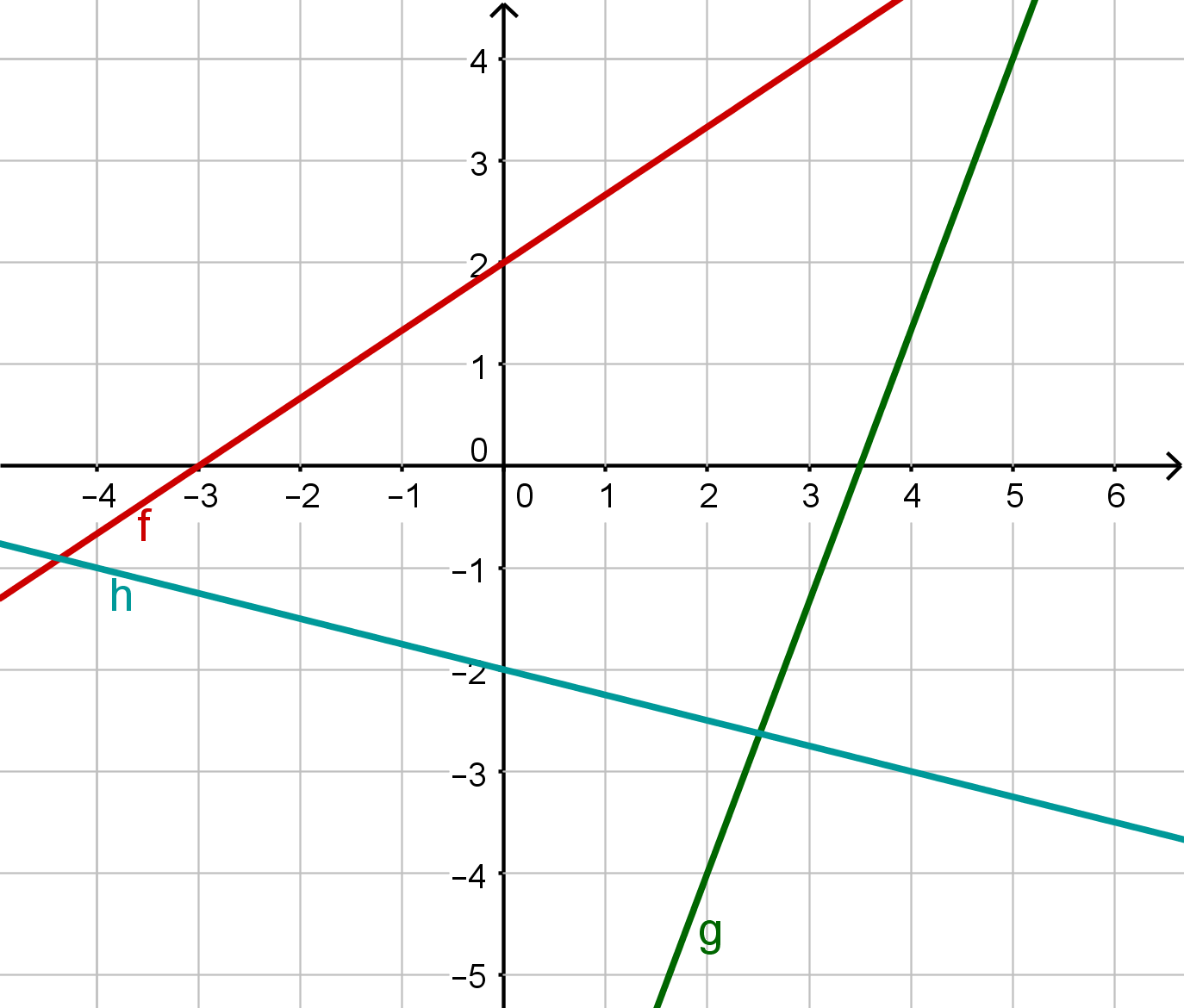
Gegeben sind die folgenden Funktionsgraphen:
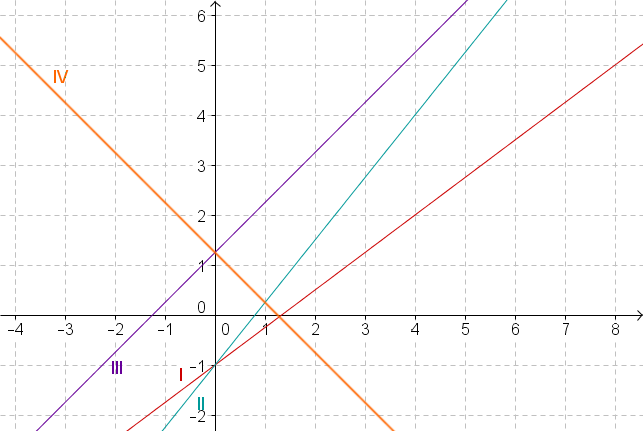
1. Welcher der vier Graphen gehört zur Gleichung $y=\frac{5}{4}x-1$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichungen
  Vorgegebene Graphengleichung: $y=\frac54x-1$
  Du kannst die Steigung und den y-Achsenabschnitt dieses Graphen an der Gleichung ablesen.
  $m=\frac{5}{4}$
  $ t = - 1$
  Überprüfe zuerst bei welchen Funktionen der y-Achsenabschnitt $t = - 1$ beträgt, indem du den y-Wert jedes Graphen abliest, indem die y-Achse geschnitten wird.
  Nur Graph I und II haben den y-Achsenabschnitt $- 1$ also kannst du jeden anderen Graphen ausschließen.
  Überprüfe nun welcher der beiden Graphen die Steigung $m=\frac54$ besitzt, indem du vom Punkt $x = 0$ ausgehend eins nach rechts gehst und überprüfst, welcher der beiden y-Werte sich um $\frac54$ erhöht.
  Beide Graphen beginnen beim Punkt $P\left(0;-1\right)$ . Da die gesuchte Gerade die Steigung $\frac54$ hat, geht sie auch durch den Punkt $(0 + 4 ∣ - 1 + 5) = (4 ∣ 4)$ .
  Durch diesen Punkt läuft nur die Gerade II.
  $\Rightarrow$ Der Graph II ist der Graph, der zu der vorgegebenen Gleichung gehört.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Wie lautet die Gleichung zum Graphen III?
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichungen
  zu überprüfende Gerade: Graph III
  Lies zuerst wo der Graph die y-Achse schneidet, um den y-Achsenabschnitt zu ermitteln.
  Der y-Wert des Punktes, indem die y-Achse geschnitten wird, beträgt $y = 1,25$ . Somit ist $t = 1,25$ .
  Lies nun ab um wieviel sich der y-Wert verändert, wenn du ausgehend von $x = 0$ , eins nach rechts gehst. Dadurch ermittelst du die Steigung.
  Der y-Wert erhöht sich von $y = 1,25$ auf $y = 2,25$ . Somit beträgt die Steigung $m=\frac{2{,}25-1{,}25}{1}=\frac11=1$ .
  Stelle die Gleichung auf.
  ⇒ Der Graph III hat die Gleichung $y = x + 1,25$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
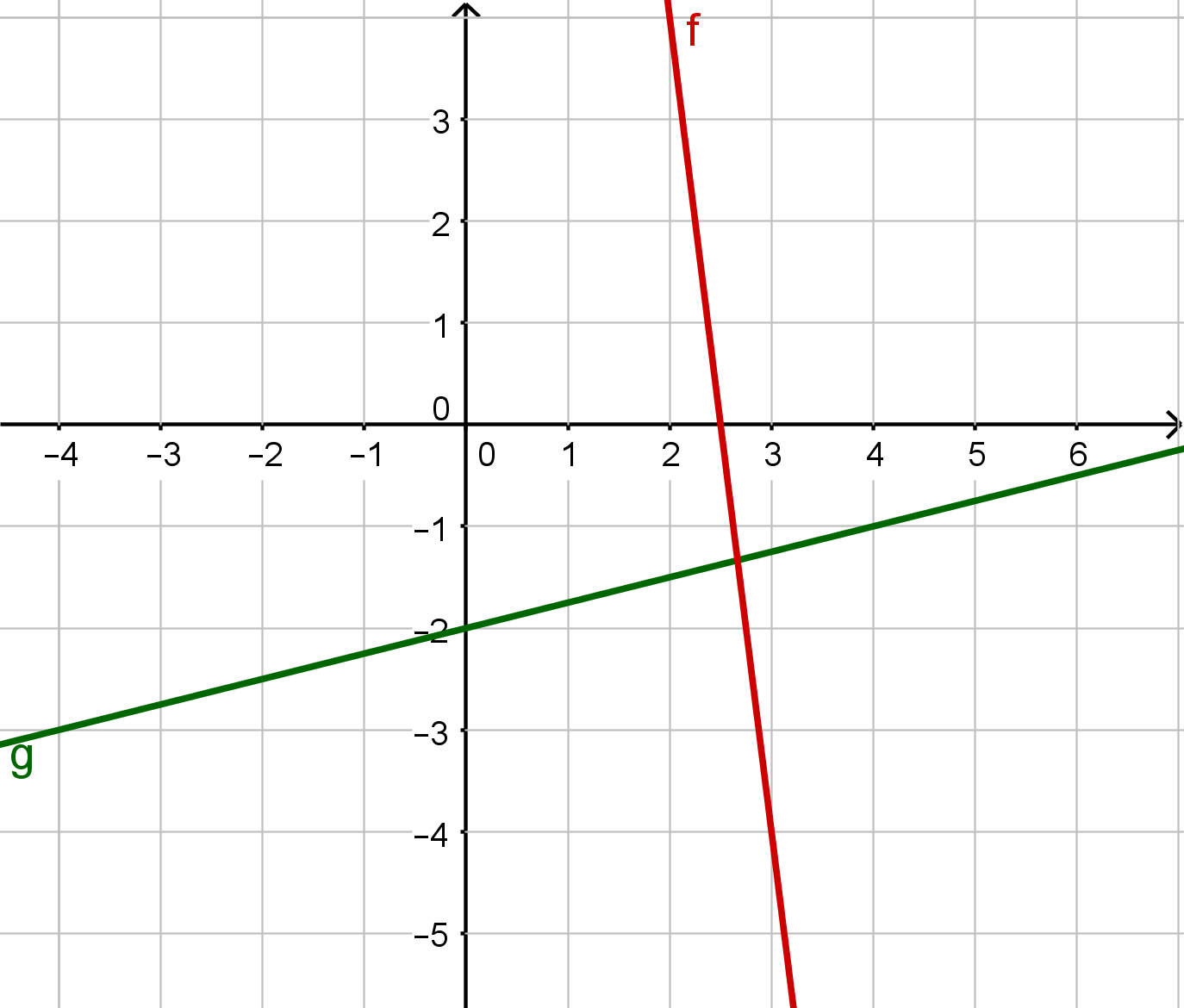
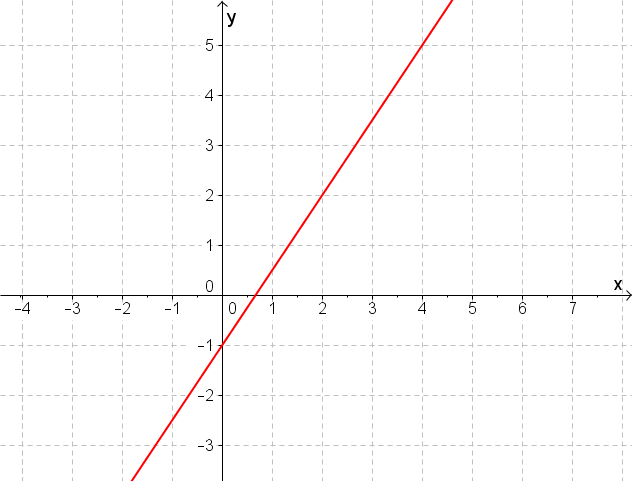
Folgende Abbildungen enthalten Graphen von linearen Funktionen.
Bestimme die Funktionsterme.
1. Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
  Lineare Funktion $f (x)$
  Stelle die allgemeine Form einer linearen Funktion auf.
  $f(x)=m \cdot x+t$
  Lies den y-Achsenabschnitt an der Abbildung ab.
  $t = 2$
  Lies zwei Punkte auf dem Graphen der linearen Funktion ab und berechne die Steigung:
  $\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1}$
  Du kannst zum Beispiel diese Punkte verwenden:
  $P_{1} (- 3 ∣ 0)$ $x_{1} = - 3$ und $y_{1} = 0$
  $P_{2} (0 ∣ 2)$ $x_{2} = 0$ und $y_{2} = 2$
  Für die Steigung erhältst du dann durch einsetzen:
  $\displaystyle m = \frac{2 - 0}{0 - (-3)} = \frac{2}{3}$
  Setze die berechneten Werte von $m$ und $t$ nun in die allgemeine Form ein:
  $f(x) = \dfrac{2}{3}\cdot x + 2$
  Lineare Funktion $g (x)$
  Stelle die allgemeine Form einer linearen Funktion auf.
  $g(x)=m \cdot x+t$
  Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um die Steigung zu berechnen.
  $\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1}$
  Beispielsweise kannst du diese beiden Punkte verwenden:
  $P_{1} (2 ∣ - 4)$ $x_{1} = 2$ und $y_{1} = - 4$
  $P_2(3{,}5|0)$ $x_2=3{,}5$ und $y_{2} = 0$
  Die Steigung ist dann:
  $\displaystyle m = \frac{0 - (-4)}{3{,}5 - 2} = \frac{4}{1{,}5} = 4 \cdot \frac{2}{3} = \frac{8}{3}$
  Da der y-Achsenabschnitt nicht sichtbar ist, musst du ihn berechnen. Stelle dafür die Geradengleichung auf.
  $\displaystyle g(x) = \frac{8}{3} \cdot x + t$
  Setze einen der Punkte ein, zum Beispiel $(2 ∣ - 4)$ .
  $\displaystyle -4 = \frac{8}{3} \cdot 2 + t$
  Löse nun nach $t$ auf.
  $\displaystyle t = -4- \frac{8}{3} \cdot 2 = -\frac{12}{3}- \frac{16}{3} = -\frac{28}{3}$
  Setze die Werte von $m$ und $t$ in die allgemeine Form der linearen Funktion ein und du bekommst die Geradengleichung:
  $\displaystyle g(x)=\frac{8}{3} \cdot x - \frac{28}{3}$
  Lineare Funktion $h (x)$
  Stelle die allgemeine Form einer linearen Funktion auf.
  $h(x)=m \cdot x+t$
  Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um die Steigung zu berechnen.
  $\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1}$
  Du kannst zum Beispiel diese beiden Punkte verwenden:
  $P_{1} (0 ∣ - 2)$ $x_{1} = 0$ und $y_{1} = - 2$
  $P_{2} (4 ∣ - 3)$ $x_{2} = 4$ und $y_{2} = - 3$
  Mit ihnen kannst du nun die Steigung berechnen:
  $\displaystyle m = \frac{-3 - (-2)}{4 - 0} = \frac{-3 + 2}{4} = -\frac{1}{4}$
  Lies entweder $t = - 2$ ab oder berechne den Wert. Um ihn zu berechnen, stelle die Geradengleichung auf.
  $\displaystyle h(x) = -\frac{1}{4} \cdot x + t$
  Setze einen Punkt ein, der auf der Gerade liegt, zum Beispiel $(4 ∣ - 3)$ .
  $\displaystyle -3 = -\frac{1}{4} \cdot 4 + t$
  Löse nun noch nach $t$ auf.
  $t = - 3 + 1 = - 2$
  Setze $m = -\dfrac14$ und $t = - 2$ in die allgemeine Form ein und du erhältst die Geradengleichung:
  $\displaystyle h(x) = -\frac{1}{4} \cdot x -2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
  Lineare Funktion $f (x)$
  Stelle die allgemeine Form einer linearen Funktion auf.
  $f(x)=m \cdot x+t$
  Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um mit ihnen die Steigung zu berechnen:
  $\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1}$
  Du kannst zum Beispiel diese beiden Punkte verwenden:
  $P_{1} (2 ∣ 4)$ $x_{1} = 2$ und $y_{1} = 4$
  $P_2(2{,}5|0)$ $x_2= 2{,}5$ und $y_{2} = 0$
  Als Steigung ergibt sich:
  $\displaystyle m = \frac{0 - 4}{2{,}5 - 2} = \frac{-4}{0{,}5} = -4 \cdot \frac{2}{1} = -8$
  Da der y-Achsenabschnitt nicht sichtbar ist, musst du ihn berechnen. Stelle daher die Geradengleichung auf:
  $\displaystyle f(x) = -8 \cdot x + t$
  Setze einen der Punkte, zum Beispiel $(2 ∣ 4)$ , ein:
  $\displaystyle 4 = -8 \cdot 2 + t$
  Löse nach $t$ auf.
  $\displaystyle t = 4 + 8 \cdot 2 = 4 + 16 = 20$
  Setze $m = - 8$ und $t = 20$ in die allgemeine Form ein und du bekommst als Ergebnis die Geradengleichung:
  $f(x) = -8\cdot x + 20$
  Lineare Funktion $g (x)$
  Stelle die allgemeine Form einer linearen Funktion auf.
  $g(x)=m \cdot x+t$
  Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um mit ihnen die Steigung zu berechnen:
  $\displaystyle m = \frac{y_2 - y_1}{x_2 - x_1}$
  Du kannst zum Beispiel diese beiden Punkte verwenden:
  $P_{1} (0 ∣ - 2)$ $x_{1} = 0$ und $y_{1} = - 2$
  $P_{2} (- 4 ∣ - 3)$ $x_{2} = - 4$ und $y_{2} = - 3$
  Berechne mit ihnen nun die Steigung:
  $\displaystyle m = \frac{-3 - (-2)}{-4 - 0} = \frac{-3 +2}{-4} = \frac{1}{4}$
  Lies den y-Achsenabschnitt an der Abbildung ab.
  $t = - 2$
  Setze $m = \dfrac14$ und $t = - 2$ in die allgemeine Form der linearen Funktion ein und du erhältst die Geradengleichung von $g$ :
  $\displaystyle g(x)=\frac{1}{4} \cdot x - 2$
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3
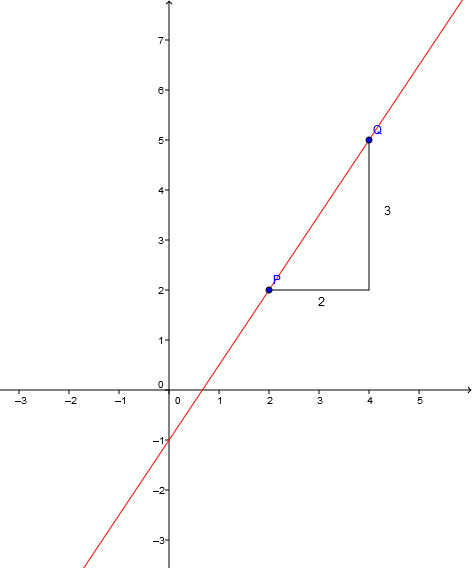
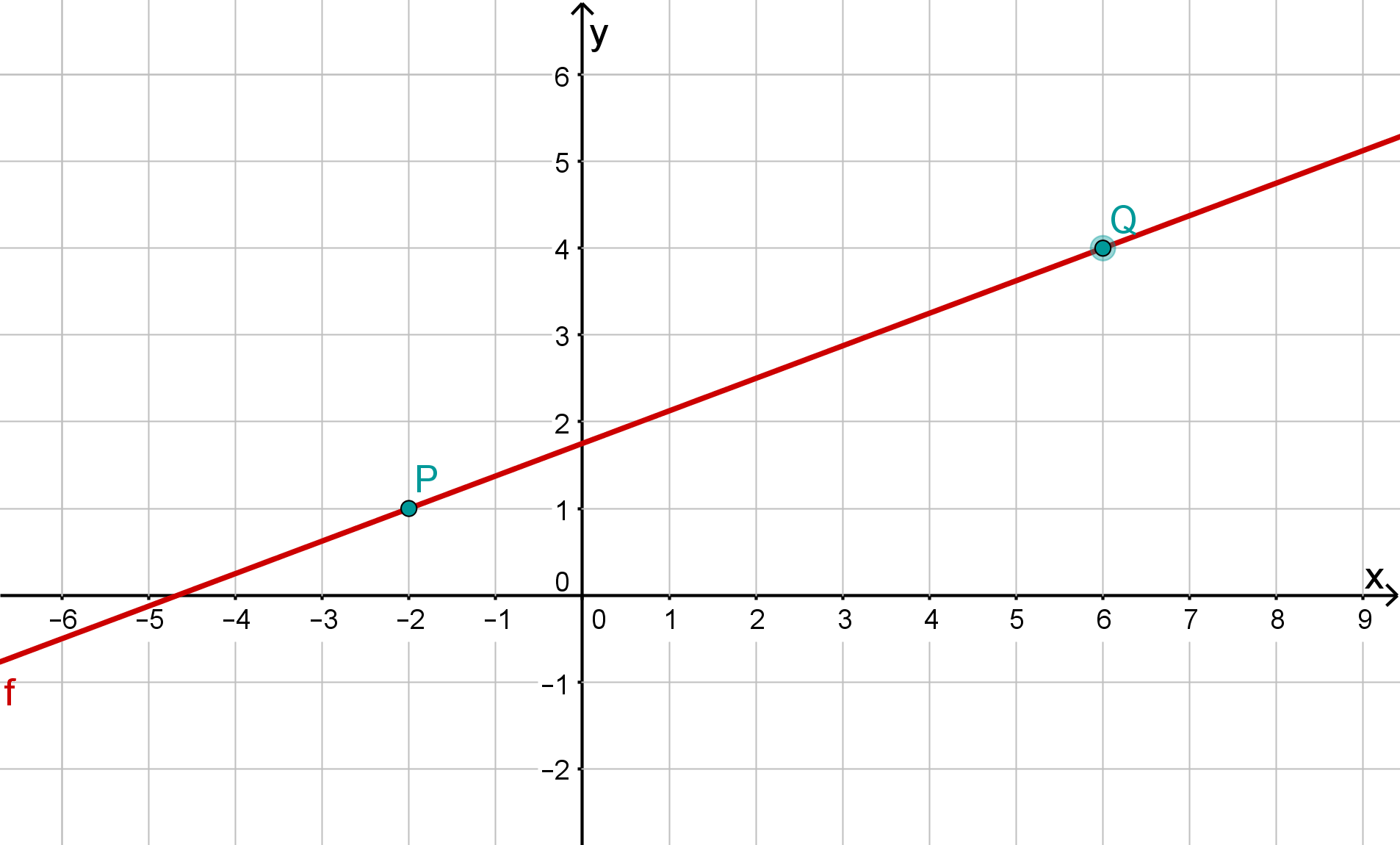
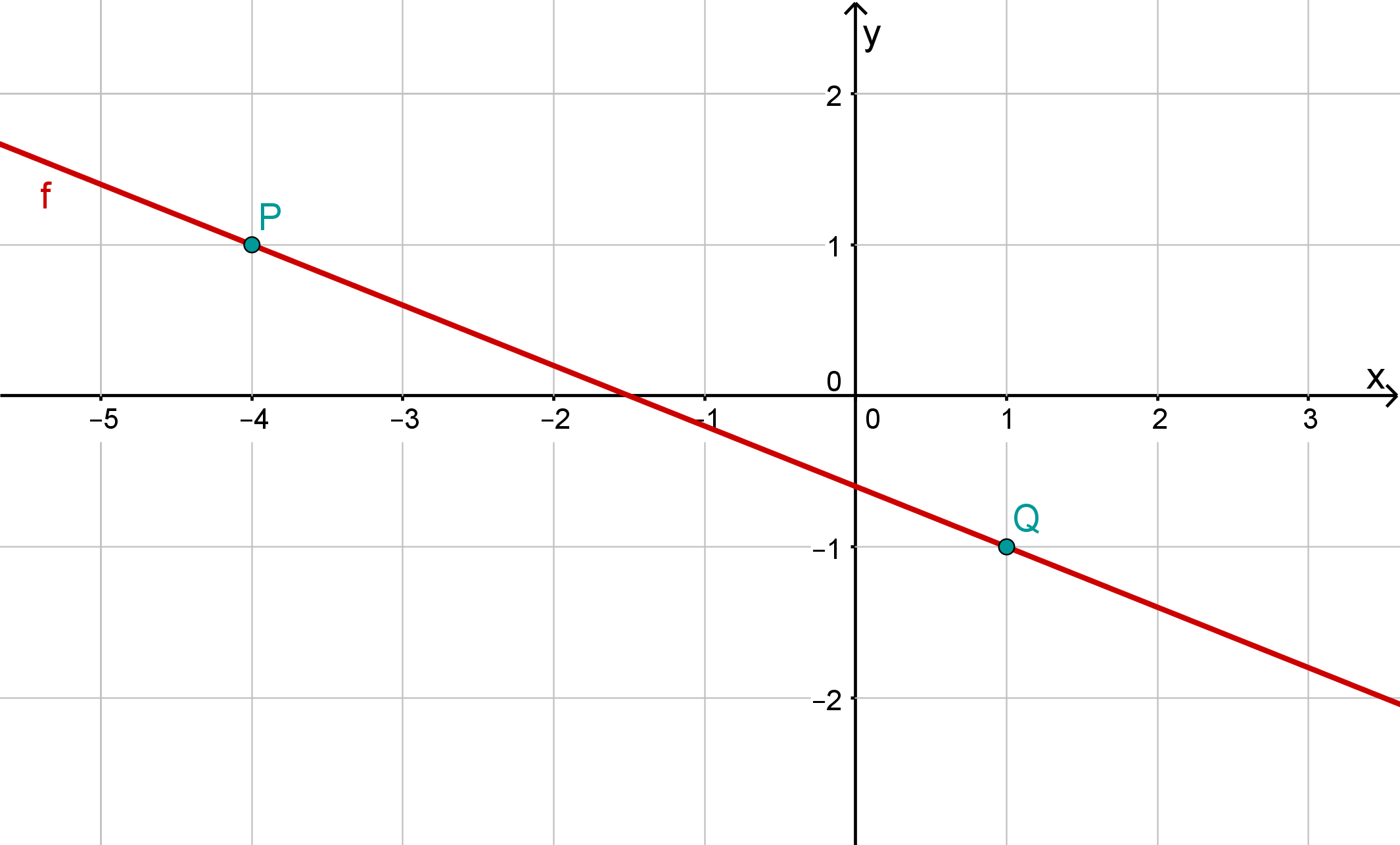
Bestimme die Gleichung folgender Gerade:

Für diese Aufgabe benötigst Du folgendes Grundwissen: Gerade im Koordinatensystem
Die allgemeine Geradengleichung ist:
$\mathrm y=\mathrm m\cdot\mathrm x+\mathrm t$
Lese den y-Achsenabschnitt $t$ , also die Stelle, an der die Gerade die y-Achse schneidet, aus der Zeichnung ab.
$t = - 1$
Suche zwei Punkte mit (bestenfalls) ganzzahligen Koordinaten.
$P\left(2 \;|\;2\right)$ und $Q(4\;| \;5)$ liegen auf der Gerade.
Um die Steigung $m$ zu bestimmen, gibt es zwei Möglichkeiten:
1. $\;m=\displaystyle\frac{y_Q-y_P}{x_Q-x_P}$
Setze die Koordinaten von $P$ und $Q$ ein!
$m=\displaystyle\frac{5-2}{4-2}=\frac32=1{,}5$
2.
Zeichne ein Steigungsdreieck zwischen den Punkten. Der senkrechte Abstand ist der Zähler, der waagerechte Abstand ist der Nenner des Bruches, der die Steigung beschreibt.
$m=\displaystyle\frac{\text{senkrecht}}{\text{waagerecht}}=\frac32=1{,}5$
Die Geradengleichung ist also gegeben durch:
$\mathrm g\left(\mathrm x\right)=\frac32\cdot\mathrm x-1=1{,}5x-1$

Berechne die Steigung der Gerade durch die gegebenen Punkte.

$A (5 ∣ 7)$ , $B (- 3 ∣ 8)$

$A (1 ∣ 2)$ , $B (3 ∣ 4)$

Für diese Aufgabe benötigst Du folgendes Grundwissen: Steigung
$A (1 ∣ 2), B (3 ∣ 4)$
Setze die Punkte in den Differenzenquotient für die Gerade ein.
$\displaystyle m$ $=$ $\displaystyle \frac{4-2}{3-1}$
↓
Vereinfache Zähler und Nenner
$\displaystyle m$ $=$ $\displaystyle \frac22$
$\displaystyle m$ $=$ $\displaystyle 1$
Die Steigung der Geraden beträgt m = 1.
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

Löse die folgenden Aufgaben.

Welche Steigung hat die Gerade durch die Punkte $P (0 ∣ 3)$ und $Q (2 ∣ - 3)$ ?

Stelle die Gleichung der Geraden durch die Punkte $P (1 ∣ 3)$ und $Q (3 ∣ - 1)$ auf.

Gegeben: Punkt $P (1 ∣ 3)$ und $Q (3 ∣ - 1)$
Berechne die Differenz der beiden x-Werte und der beiden y-Werte, um die Steigung zu bestimmen.
x-Werte: $3 - 1 = 2$
y-Werte: $- 1 - 3 = - 4$
Während der x-Wert um $2$ steigt, nimmt der y-Wert um $4$ ab. Dividiere den y-Wert durch den x-Wert, um die Steigung auszurechnen.
$m=\frac{-4}{2}=-2$
Setze m, den x-Wert und den y-Wert eines der Punkte in die allgemeine Geradengleichung ein, um $t$ zu bestimmen.
$\displaystyle 3$ $=$ $\displaystyle -2\cdot1+t$
$\displaystyle 3$ $=$ $\displaystyle -2+t$ $\displaystyle +2$
$\displaystyle t$ $=$ $\displaystyle 5$
Setze $m$ und $t$ in die allgemeine Geradengleichung ein, um die Gleichung der Funktion aufzustellen.
$y = - 2 x + 5$
Hast du eine Frage oder Feedback?
Kommentiere hier 👉

6
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Welche Steigung hat die Gerade durch die Punkte $\mathrm{P}\left(0|3\right)$ und $\mathrm{Q}\left(2|-3\right)$ ? Wie lautet also die Funktionsgleichung?

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Steigung
Bestimme die Steigung $\mathrm m$ .
$\mathrm m=\dfrac{\bigtriangleup\mathrm y}{\bigtriangleup\mathrm x}=\dfrac{{\mathrm y}_2-{\mathrm y}_1}{{\mathrm x}_2-{\mathrm x}_1}$
Setze die beiden Punkte in die Formel für die Steigung ein.
$\mathrm m=\dfrac{3-(-3)}{0-2}=\dfrac 6 {-2}=-3$
Funktionsgleichung
Bestimme die Funktionsgleichung.
$\mathrm y=\mathrm m\cdot\mathrm x+\mathrm t$
Setze m in die allgemeine Geradengleichung ein.
$\mathrm y=-3\mathrm x+\mathrm t$
Setze einen der beiden Punkte in die Funktionsgleichung ein.
$3=-3\cdot0+\mathrm t$
$\mathrm t=3$
Setze t in die Funktionsgleichung ein.
$\;\;\Rightarrow\;\;\mathrm f\left(\mathrm x\right)=-3\mathrm x+3$
7
strobl-f.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Franz Strobl
Stelle die Gleichung der Geraden durch die Punkte $\mathrm P\left(1| 3\right)$ und $\mathrm Q\left(3|-1\right)$ auf.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Gegeben sind die beiden Punkte $P(1\mid 3)$ und $Q(3\mid -1)$ .
Gesucht ist die Gleichung der Geraden, die durch die beiden Punkte geht.
Zur Ermittlung der Geradengleichung überlegst du am Besten erst die allgemeine Form der Geradengleichung:
Bestimmung der Steigung $m$
Erinnere dich zunächst an die Gleichung für die Steigung einer Geraden:
$\displaystyle m=\frac{y_2-y_1}{x_2-x_1}$
Setze die Werte $x_{1}, x_{2}, y_{1}, y_{2}$ aus den Punkten $P$ und $Q$ in die Formel ein.
$m=\frac{-1-3}{3-1}=\ \frac{-4}{2}$
Kürze den Bruch.
$m = - 2$
Jetzt weißt du, dass die Gleichung der Geraden durch die Punkte $P$ und $Q$ geht folgendermaßen aussieht:
$\displaystyle y=-2\cdot x+t.$
Als nächstes ermittelst du den $y$ -Achsenabschnitt ( $t$ ).
Ermittlung des $y$ -Achsenabschnitts $t$
Um $t$ zu ermitteln setzt du den $x$ - und $y$ -Wert einer der beiden Punkte in die Geradengleichung ein. Hier wird das beispielhaft mit dem Punkt $P$ ausgerechnet.
$3=-2\cdot 1+t$
$3 = - 2 + t$
$t = 5$
Der $y$ -Achsenabschnitt der Funktion ist $5$ . Damit hast du auch schon die ganze Funktionsgleichung.
$y=-2\cdot x +5$

Stelle die Gleichung der Geraden mit Steigung $m=-\frac43$ durch den Punkt $P (- 2 ∣ - 0,5)$ auf und zeichne sie in ein Koordinatensystem.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung erstellen

Geradengleichung erstellen

$m=-\frac43$ ; $P (- 2 ∣ - 0,5)$

Setze $m$ und $P$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.

$\displaystyle -\frac{1}{2}$	$=$	$\displaystyle -\frac{4}{3}\cdot\left(-2\right)+t$
	↓	$-\frac{4}{3}\cdot\left(-2\right)=\frac{\left(-4\right)\cdot\left(-2\right)}{3}=\frac{8}{3}$
$\displaystyle -\frac{1}{2}$	$=$	$\displaystyle \frac{8}{3}+t$	$\displaystyle -\frac{8}{3}$
$\displaystyle t$	$=$	$\displaystyle -\frac{1}{2}-\frac{8}{3}$
	↓	Bringe die beiden Brüche auf denselben Nenner.
$\displaystyle t$	$=$	$\displaystyle -\frac{3}{6}-\frac{16}{6}$
	↓	Subtrahiere.
$\displaystyle t$	$=$	$\displaystyle -\frac{19}{6}$
	↓	Wandle in einen gemischten Bruch um.
$\displaystyle t$	$=$	$\displaystyle -3\ \frac{1}{6}$
	↓	Setze t und m in die allgemeine Geradengleichung ein.

$\;\;\Rightarrow\;\;$ $y=-\frac43x-3\frac16$

Gerade zeichnen

Wähle einen beliebigen Punkt auf der Geraden, z. B. den gegebenen Punkt $P (- 2 ∣ - 0,5)$ . Einen zweiten Punkt findest du, indem du vom Punkt $P$ aus entsprechend der Steigung $m=-\frac{4}{3}$ , um $1$ nach rechts und um $\dfrac{4}{3}$ nach unten gehst. Du erhältst das $\textcolor{006400}{\text{grüne Steigungsdreieck}}$ . Verbinde die beiden Punkte zu einer Geraden.

Einfacher findest du den zweiten Punkt, indem du um $3$ nach rechts und $4$ nach unten gehst. Du erhältst das $\textcolor{ff6600}{\text{orangefarbige Steigungsdreieck}}$ . (Die Steigung ist dann immer noch $m=-\frac{4}{3}$ .)

Hast du eine Frage oder Feedback?

Bitte melde dich an, um diese Funktion zu benutzen.

9
Stelle die Gleichung der Geraden auf, die durch den Punkt $P(-3\vert3)$ verläuft und die Steigung $m = - 2$ hat. Zeichne die Gerade.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
1. Setze $m$ und die Koordinaten des Punktes $P$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.
$\displaystyle \def\arraystretch{1.25} \begin{array}{l}\begin{array}{ccccc}\mathrm y&=&\mathrm m\cdot\mathrm x+\mathrm t&&\\3&=&(-2)\cdot(-3)+\mathrm t&\;\;\;\;\;\left|-6\right.&\;\\3-6&=&\mathrm t\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;&\;\;&\;\end{array}\\\begin{array}{ccc}\;\;\;\;\;\;\;\mathrm t&=&-3\;\;\;\;\;\;\;\end{array}\\\end{array}$
2. Setze $m$ und $t$ in die allgemeine Geradengleichung ein $\Rightarrow \;\;y=-2x-3$
Gerade zeichnen
Zeichne den gegebenen Punkt $P(-3\vert3)$ in das Koordinatensystem ein. Zeichne dann ein Steigungsdreieck, indem Du um $1$ nach rechts und um $2$ nach unten gehst $(m = - 2)$ . Trage dort den Punkt $Q$ ab. Verbinde $P$ und $Q$ zu einer Geraden.
10
Stelle die Gleichung der Geraden durch die zwei Punkte auf und zeichne sie.
1. $P (2 ∣ 0)$ und $Q (- 2 ∣ 2)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Geradengleichung ermitteln
  $P (2 ∣ 0); Q (- 2 ∣ 2)$
  Ermittle die Steigung $m$ der allgemeinen Geradengleichung $y=m\cdot x+t$ mithilfe des Differenzenqotienten .
  $m=\frac{2-0}{-2-2}=\frac2{-4}=-\frac12$
  Setze $m$ und die Koordinaten eines Punktes z. B. $P (2 ∣ 0)$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.
  $0=-\frac{1}{2}\cdot2+t\ \;\;\;\;\;\left|{+\frac12\cdot2}\right.$
  $t = 1$
  Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
  $\;\;\Rightarrow\;\;$ $y=-\frac12x+1$
  Gerade zeichnen
  Zeichne die beiden vorgegebenen Punkte $P (2 ∣ 0)$ und $Q (- 2 ∣ 2)$ in das Koordinatensystem ein und verbinde sie zu einer Geraden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
2. $P (0,5 ∣ 1,5)$ und $Q (5 ∣ 3)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Geradengleichung ermitteln
  $P (0,5 ∣ 1,5); Q (5 ∣ 3)$
  Ermittle die Steigung $m$ der allgemeinen Geradengleichung $y=m\cdot x+t$ mithilfe des Differenzenqotienten.
  $m=\frac{3-1{,}5}{5-0{,}5}=\frac{1{,}5}{4{,}5}=\frac13$
  Setze $m$ und die Koordinaten eines Punktes z. B. $Q (5 ∣ 3)$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.
  $3=\frac13\cdot5+t \;\;\;\;\;\;\;\;|{-\frac13\cdot5}$
  $t=\frac43$
  Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
  $\;\;\Rightarrow\;\;$ $y=\frac13x+\frac43$
  Gerade zeichnen
  Zeichne die beiden vorgegebenen Punkte $P (0,5 ∣ 1,5)$ und $Q (5 ∣ 3)$ in das Koordinatensystem ein und verbinde sie zu einer Geraden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
3. $P (- 2 ∣ 1)$ und $Q (6 ∣ 4)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Geradengleichung ermitteln
  $P (- 2 ∣ 1)$ ; $Q (6 ∣ 4)$
  Ermittle die Steigung $m$ der allgemeinen Geradengleichung $y=m\cdot x+t$ mithilfe des Differenzenqotienten .
  $m=\frac{4-1}{6-(-2)}=\frac38$
  Setze $m$ und die Koordinaten eines Punktes z. B. $P (- 2 ∣ 1)$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.
  $1=\frac38\cdot(-2)+t$
  $1= -\frac68 +t$
  $1=-\frac34+t \;\;\;\;\;\;\;\;\;|+\frac3 4$
  $t=\frac74$
  Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
  $\;\;\Rightarrow\;\;$ $y=\frac38x+\frac74$
  Gerade zeichnen
  Zeichne die beiden vorgegebenen Punkte $P (- 2 ∣ 1)$ und $Q (6 ∣ 4)$ in das Koordinatensystem ein und verbinde sie zu einer Geraden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
4. $P (- 4 ∣ 1)$ und $Q (1 ∣ - 1)$
  
  Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
  Geradengleichung ermitteln
  $P (- 4 ∣ 1)$ ; $Q (1 ∣ - 1)$
  Ermittle die Steigung $m$ der allgemeinen Geradengleichung $y=m\cdot x+t$ mithilfe des Differenzenqotienten.
  $m=\frac{-1-1}{1-(-4)}=-\frac25$
  Setze $m$ und die Koordinaten eines Punktes z. B. $P (- 4 ∣ 1)$ in die allgemeine Geradengleichung ein und löse nach $t$ auf.
  $1=-\frac25\cdot(-4)+t$
  $1=\frac85+t \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;|- \frac 8 5$
  $t=-\frac35$
  Setze $m$ und $t$ in die allgemeine Geradengleichung ein.
  $\;\;\Rightarrow\;\;$ $y=-\frac25x-\frac35$
  Gerade zeichnen
  Zeichne die beiden vorgegebenen Punkte $P (- 4 ∣ 1)$ und $Q (1 ∣ - 1)$ in das Koordinatensystem ein und verbinde sie zu einer Geraden.
  Hast du eine Frage oder Feedback?
  Kommentiere hier 👉
11
Gegeben sind der $y$ -Achsenabschnitt $t = 2$ und der Punkt $P(3\vert-1)$ . Berechne die zugehörende Geradengleichung und zeichne die Gerade.
ist die Gleichung der Geraden.

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
1. Setze $t$ und die Koordinaten des Punktes $P$ in die allgemeine Geradengleichung ein und löse nach $m$ auf.
$\displaystyle \def\arraystretch{2} \begin{array}{l}\begin{array}{ccccc}\ y&=&\mathrm m\cdot\mathrm x+\mathrm t&&\\-1&=&\mathrm m\cdot3+2&\left|-2\right.&\;\\-1-2&=&\;\;\;\;\;\;\mathrm m\cdot 3\;\;\;\;\;\;\;\left|:3\right.&\;\end{array}\\\begin{array}{ccc}\;\;\;\;\;\;\;\mathrm m\;\;\;\; =\dfrac{-3}{3}=-1\;\;\;\;\;\;\;\end{array}\\\end{array}$
2. Setze $m$ und $t$ in die allgemeine Geradengleichung ein $\Rightarrow\;\;y=-x+2$
Gerade zeichnen
Zeichne den gegebenen Punkt $P(3\vert-1)$ in das Koordinatensystem ein. Zeichne dann den Punkt $S_y(0\vert2)$ ( $y$ -Achsenabschnitt $t = 2$ ) ebenfalls ein und verbinde die Punkte $S_{y}$ und $P$ zu einer Geraden.
12
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
Für eine lineare Funktion $\mathrm h\left(\mathrm x\right)$ gilt:
$\mathrm h\left(0\right)=3$ und $\mathrm h\left(-2\right)=4$ . Bestimmen Sie $\mathrm h\left(\mathrm x\right)$ .

Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichungen
Bestimme den y-Achsenabschnitt t
Bei einer Funktion ist der y-Achsenabschnitt gleich dem Wert bei x=0.
$t = h (0) = 3$
Bestimme jetzt mit den zwei gegebenen Punkten die Steigung m mit dem Differenzenquotienten.
$m=\frac{3-4}{0-(-2)}=\frac{-1}{2}=-\frac12$
Setze zur Geradengleichung zusammen.
$\Rightarrow y=-\frac12 x+3$

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?

$\displaystyle -3$	$=$	$\displaystyle m\cdot2+3$	$\displaystyle -3$
$\displaystyle -6$	$=$	$\displaystyle m\cdot2$	$\displaystyle :2$
$\displaystyle -3$	$=$	$\displaystyle m$

$\displaystyle m$	$=$	$\displaystyle \frac{8-7}{-3-5}$
	↓	Vereinfache Zähler und Nenner
$\displaystyle m$	$=$	$\displaystyle \frac{1}{-8}$
$\displaystyle m$	$=$	$\displaystyle - \frac18$

$\displaystyle m$	$=$	$\displaystyle \frac{4-2}{3-1}$
	↓	Vereinfache Zähler und Nenner
$\displaystyle m$	$=$	$\displaystyle \frac22$
$\displaystyle m$	$=$	$\displaystyle 1$

$\displaystyle 3$	$=$	$\displaystyle -2\cdot1+t$
$\displaystyle 3$	$=$	$\displaystyle -2+t$	$\displaystyle +2$
$\displaystyle t$	$=$	$\displaystyle 5$

Aufgaben zum Aufstellen der Geradengleichung

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Lineare Funktion f(x)f(x)f(x)

Lineare Funktion g(x)g(x)g(x)

Lineare Funktion h(x)h(x)h(x)

Hast du eine Frage oder Feedback?

Lineare Funktion f(x)f(x)f(x)

Lineare Funktion g(x)g(x)g(x)

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Hast du eine Frage oder Feedback?

Steigung

Funktionsgleichung

Bestimmung der Steigung mmm

Ermittlung des yyy-Achsenabschnitts ttt

Geradengleichung erstellen

Gerade zeichnen

Gerade zeichnen

Geradengleichung ermitteln

Gerade zeichnen

Hast du eine Frage oder Feedback?

Geradengleichung ermitteln

Gerade zeichnen

Hast du eine Frage oder Feedback?

Geradengleichung ermitteln

Gerade zeichnen

Hast du eine Frage oder Feedback?

Geradengleichung ermitteln

Gerade zeichnen

Hast du eine Frage oder Feedback?

Gerade zeichnen

Lineare Funktion $f (x)$

Lineare Funktion $g (x)$

Lineare Funktion $h (x)$

Lineare Funktion $f (x)$

Lineare Funktion $g (x)$

Bestimmung der Steigung $m$

Ermittlung des $y$ -Achsenabschnitts $t$