Folgende Abbildungen enthalten Graphen von linearen Funktionen.
Bestimme die Funktionsterme.
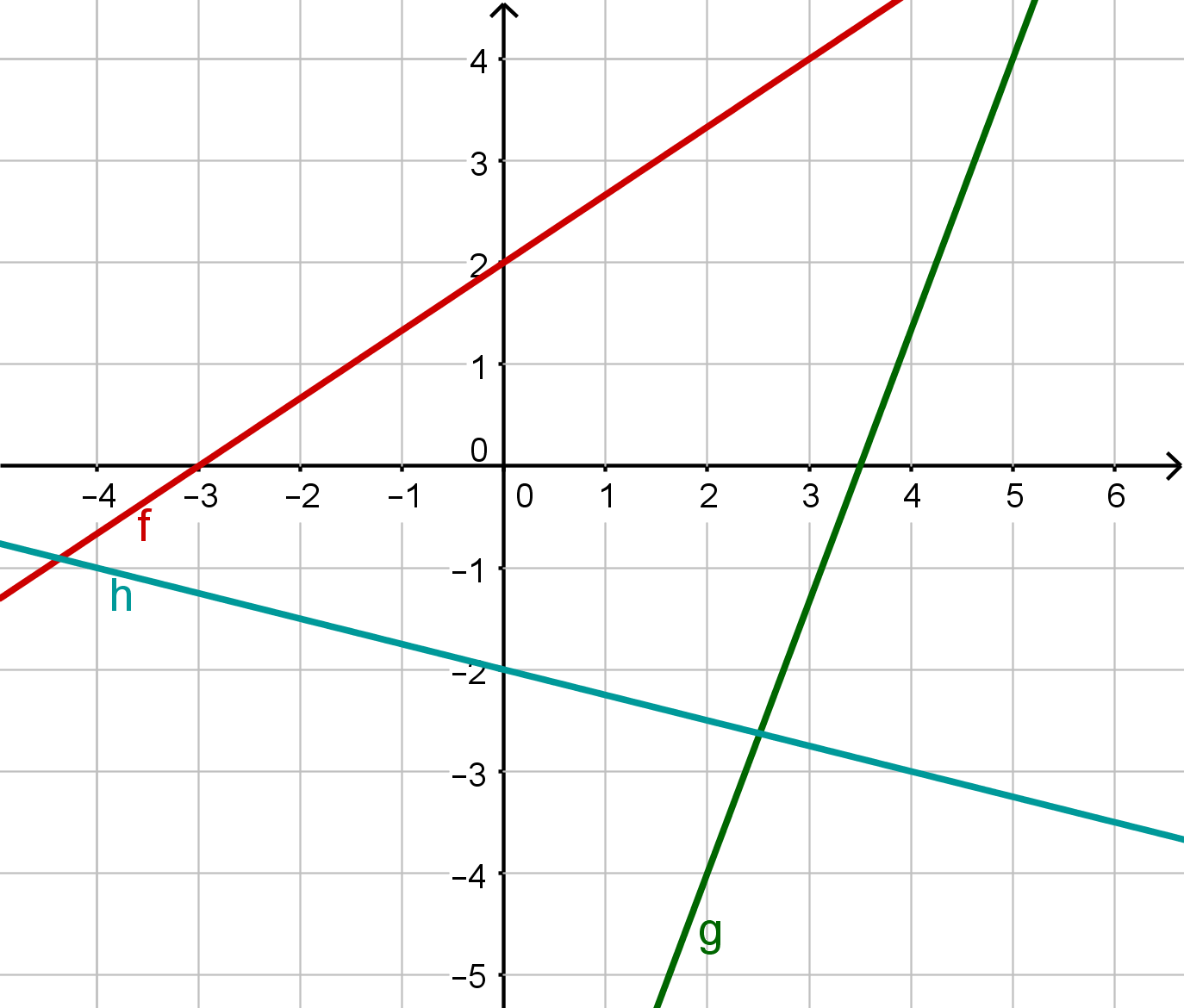
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Lineare Funktion
Stelle die allgemeine Form einer linearen Funktion auf.
Lies den y-Achsenabschnitt an der Abbildung ab.
Lies zwei Punkte auf dem Graphen der linearen Funktion ab und berechne die Steigung:
Du kannst zum Beispiel diese Punkte verwenden:
und
und
Für die Steigung erhältst du dann durch einsetzen:
Setze die berechneten Werte von und nun in die allgemeine Form ein:
Lineare Funktion
Stelle die allgemeine Form einer linearen Funktion auf.
Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um die Steigung zu berechnen.
Beispielsweise kannst du diese beiden Punkte verwenden:
und
und
Die Steigung ist dann:
Da der y-Achsenabschnitt nicht sichtbar ist, musst du ihn berechnen. Stelle dafür die Geradengleichung auf.
Setze einen der Punkte ein, zum Beispiel .
Löse nun nach auf.
Setze die Werte von und in die allgemeine Form der linearen Funktion ein und du bekommst die Geradengleichung:
Lineare Funktion
Stelle die allgemeine Form einer linearen Funktion auf.
Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um die Steigung zu berechnen.
Du kannst zum Beispiel diese beiden Punkte verwenden:
und
und
Mit ihnen kannst du nun die Steigung berechnen:
Lies entweder ab oder berechne den Wert. Um ihn zu berechnen, stelle die Geradengleichung auf.
Setze einen Punkt ein, der auf der Gerade liegt, zum Beispiel .
Löse nun noch nach auf.
Setze und in die allgemeine Form ein und du erhältst die Geradengleichung:
Hast du eine Frage oder Feedback?
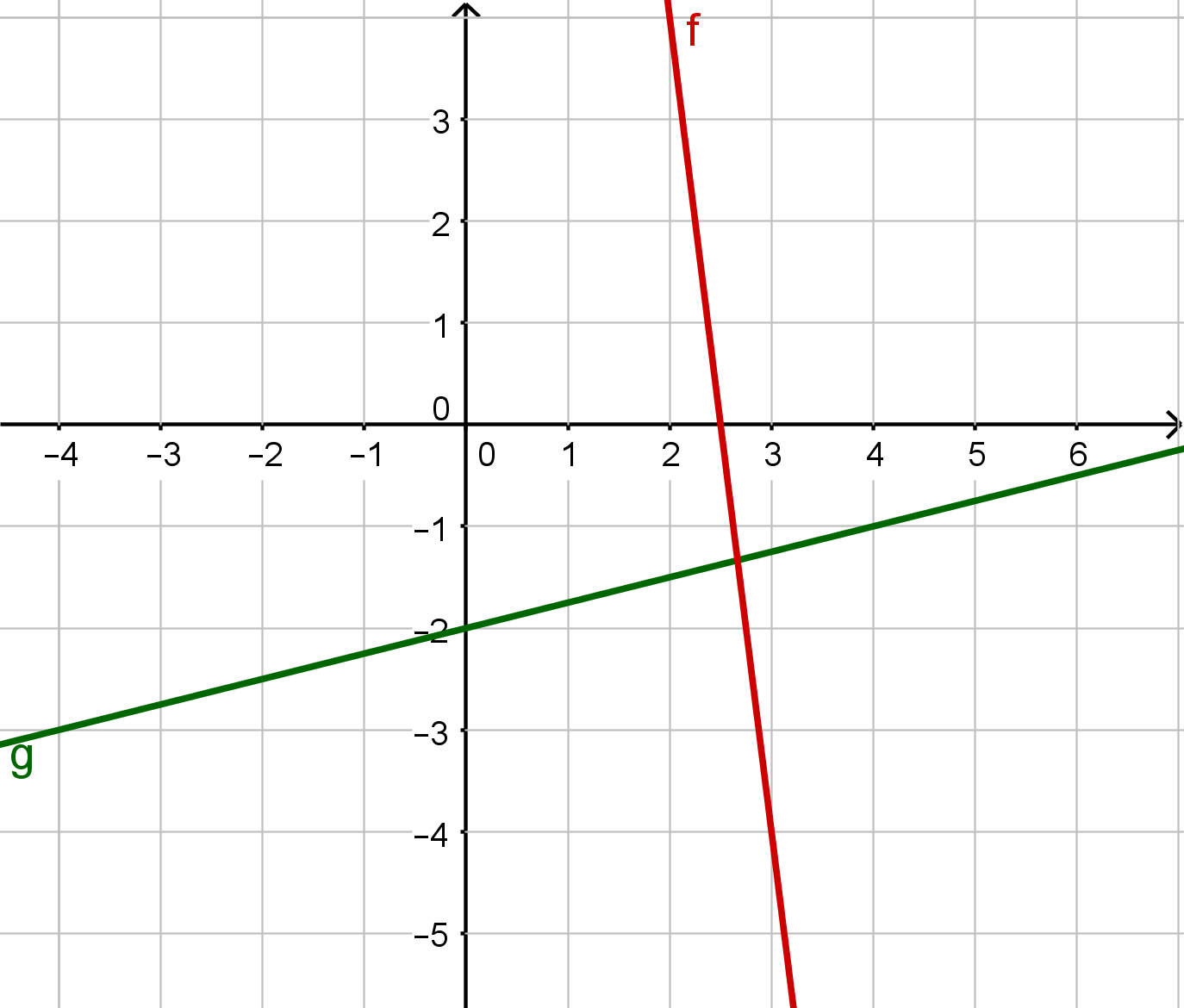
Für diese Aufgabe benötigst Du folgendes Grundwissen: Lineare Funktionen
Lineare Funktion
Stelle die allgemeine Form einer linearen Funktion auf.
Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um mit ihnen die Steigung zu berechnen:
Du kannst zum Beispiel diese beiden Punkte verwenden:
und
und
Als Steigung ergibt sich:
Da der y-Achsenabschnitt nicht sichtbar ist, musst du ihn berechnen. Stelle daher die Geradengleichung auf:
Setze einen der Punkte, zum Beispiel , ein:
Löse nach auf.
Setze und in die allgemeine Form ein und du bekommst als Ergebnis die Geradengleichung:
Lineare Funktion
Stelle die allgemeine Form einer linearen Funktion auf.
Lies zwei Punkte auf dem Graphen der linearen Funktion ab, um mit ihnen die Steigung zu berechnen:
Du kannst zum Beispiel diese beiden Punkte verwenden:
und
und
Berechne mit ihnen nun die Steigung:
Lies den y-Achsenabschnitt an der Abbildung ab.
Setze und in die allgemeine Form der linearen Funktion ein und du erhältst die Geradengleichung von :
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?
