Stelle die Gleichung der Geraden durch die zwei Punkte auf und zeichne sie.
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Geradengleichung ermitteln
Ermittle die Steigung der allgemeinen Geradengleichung mithilfe des Differenzenqotienten .
Setze und die Koordinaten eines Punktes z. B. in die allgemeine Geradengleichung ein und löse nach auf.
Setze und in die allgemeine Geradengleichung ein.
Gerade zeichnen
Zeichne die beiden vorgegebenen Punkte und in das Koordinatensystem ein und verbinde sie zu einer Geraden.
Hast du eine Frage oder Feedback?
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Geradengleichung ermitteln
Ermittle die Steigung der allgemeinen Geradengleichung mithilfe des Differenzenqotienten.
Setze und die Koordinaten eines Punktes z. B. in die allgemeine Geradengleichung ein und löse nach auf.
Setze und in die allgemeine Geradengleichung ein.
Gerade zeichnen
Zeichne die beiden vorgegebenen Punkte und in das Koordinatensystem ein und verbinde sie zu einer Geraden.
Hast du eine Frage oder Feedback?
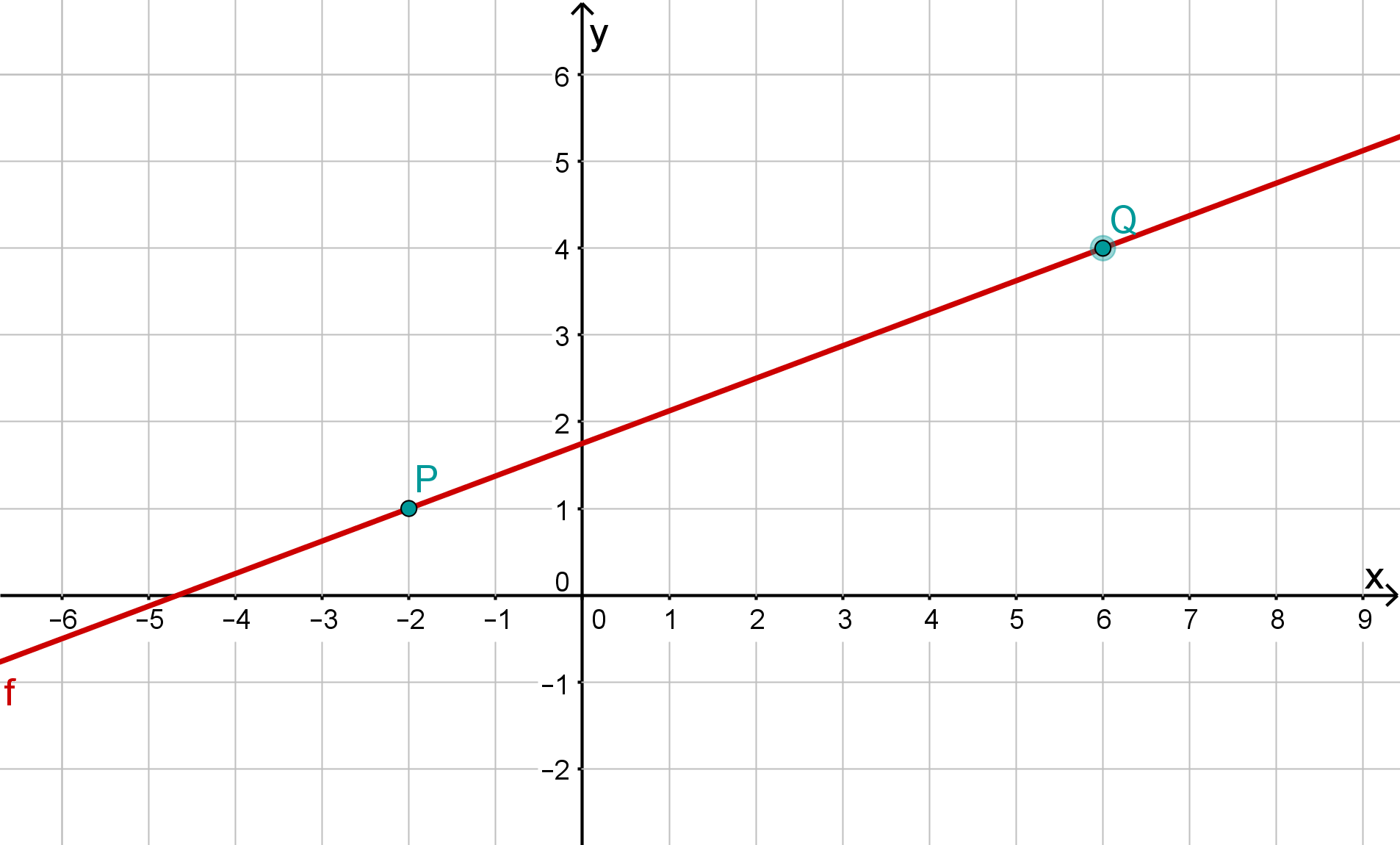
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Geradengleichung ermitteln
;
Ermittle die Steigung der allgemeinen Geradengleichung mithilfe des Differenzenqotienten .
Setze und die Koordinaten eines Punktes z. B. in die allgemeine Geradengleichung ein und löse nach auf.
Setze und in die allgemeine Geradengleichung ein.
Gerade zeichnen
Zeichne die beiden vorgegebenen Punkte und in das Koordinatensystem ein und verbinde sie zu einer Geraden.
Hast du eine Frage oder Feedback?
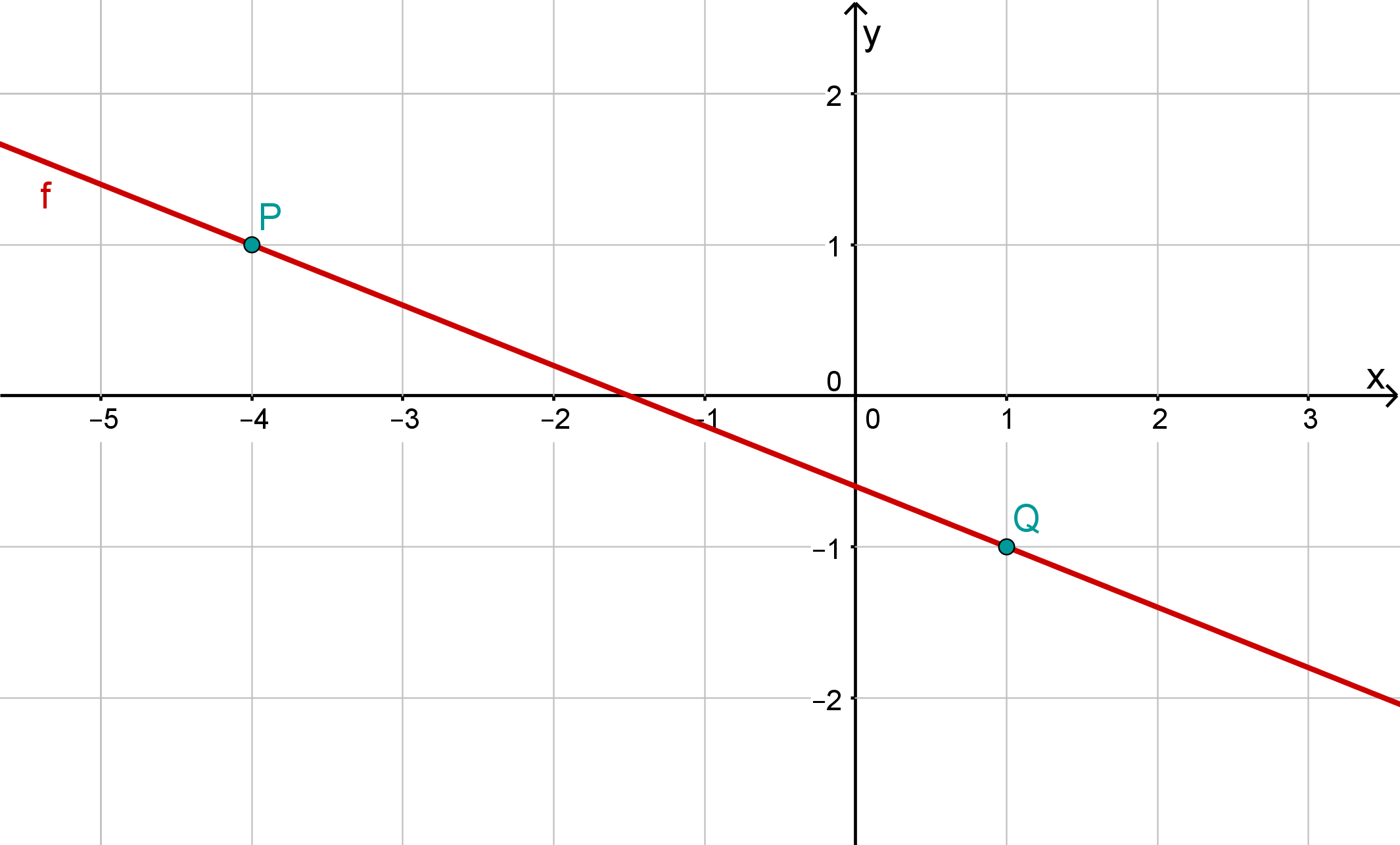
und
Für diese Aufgabe benötigst Du folgendes Grundwissen: Geradengleichung
Geradengleichung ermitteln
;
Ermittle die Steigung der allgemeinen Geradengleichung mithilfe des Differenzenqotienten.
Setze und die Koordinaten eines Punktes z. B. in die allgemeine Geradengleichung ein und löse nach auf.
Setze und in die allgemeine Geradengleichung ein.
Gerade zeichnen
Zeichne die beiden vorgegebenen Punkte und in das Koordinatensystem ein und verbinde sie zu einer Geraden.
Hast du eine Frage oder Feedback?
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?


