Die Extrema eines Funktionsgraphen sind deren Hoch- und Tiefpunkte. Hierbei wird zwischen relativen und absoluten Extrema unterschieden.
Um die Lage und Art der Extremstellen zu bestimmen, musst du folgende Schritte abhandeln:
Funktion ableiten
Nullstellen der Ableitung bestimmen
Nachweis und Art über 2. Ableitung, Monotonietabelle oder Skizze
y-Koordinate der Extremstelle durch Einsetzen der Werte in die Ausgangsfunktion
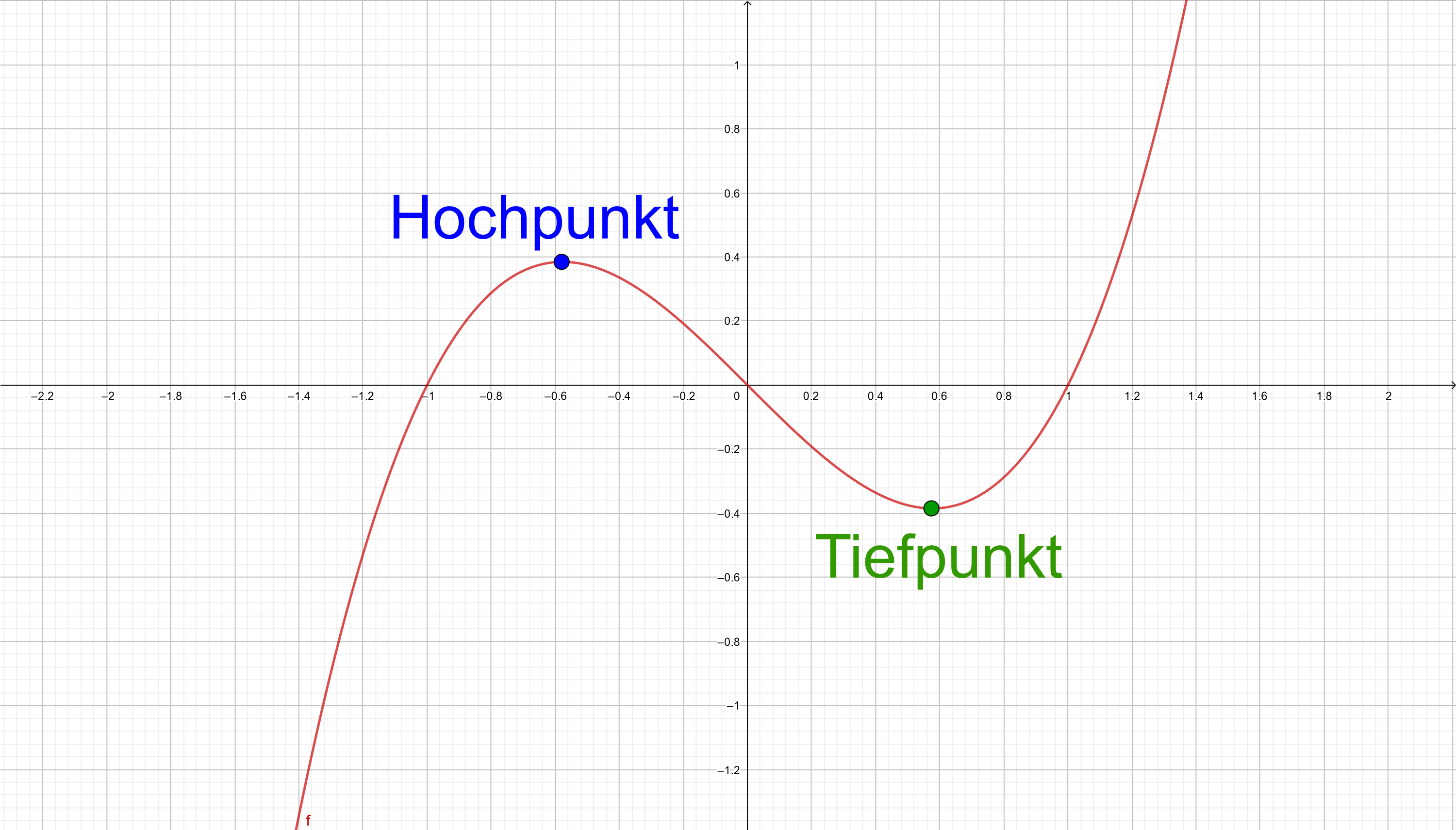
Kandidaten für Extremstellen
Extrempunkte des Graphen sind die Punkte, in denen der Graph weder fällt noch steigt. Die Steigung ist an dieser Stelle ist also gleich 0.
Die Steigung an jeder Stelle des Graphen kannst du mithilfe der Ableitung bestimmen.
Du suchst bei der Ermittlung der Extrema also die Nullstellen der 1. Ableitung!
(Dieses Kriterium wird auch notwendiges Kriterium genannt)
Nachweis und Art
Um zu überprüfen, ob tatsächlich ein Extremum vorliegt (und nicht etwa ein Terassenpunkt), hast du 3 Möglichkeiten:
Mithilfe der 2. Ableitung
Mithilfe einer Monotonietabelle
Mithilfe einer Skizze
Berechnung der y-Werte
Du berechnest den y-Wert des möglichen Extremums an der Stelle durch Einsetzen des erhaltenen x-Wertes in die Funktion :
.
Absolute Extrema
Wie du entscheiden kannst, ob ein Extrempunkt auch ein absoluter Extrempunkt ist, kannst du im Artikel relative und absolute Extrempunkte nachlesen. Dabei sind bei eingeschränkten Definitionsmengen auch die Randextrema zu beachten.
Beispiele zur Berechnung von Extrema
Beispielaufgabe 1
Bestimme das Extremum der Funktion .
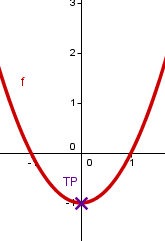
Beispiel | Allgemein |
|---|---|
Bestimmung der 1. Ableitung | |
Bestimmung der Nullstelle der 1. Ableitung | |
Einsetzen von in die 2. Ableitung bei ist ein Tiefpunkt | |
Bestimmung der y-Koordinate |
Beispielaufgabe 2
Untersuche die Funktion auf Extrema.

Beispiel | Allgemein |
|---|---|
Bestimmung und Nullsetzen der 1. Ableitung | |
| Bestimmung der 2. Ableitung und Einsetzen von |
Bestimmung der y-Koordinate |
Da das Kriterium mit der . Ableitung keine Auskunft gibt, muss ein Vorzeichenwechsel um die Extremstelle untersucht werden. Hier ergibt sich ein Sattelpunkt bzw. Terrassenpunkt.
Beispielaufgabe 3
Untersuche die Funktion auf Extrempunkte.
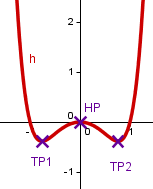
Beispiel | Allgemein |
|---|---|
| Bestimmung und Nullsetzen der 1. Ableitung |
| Bestimmung der 2. Ableitung und Einsetzen der x-Werte. Bei ist ein Hochpunkt und bei und sind Tiefpunkte. |
| Bestimmung der y-Koordinaten. Die Punkte werden vollständig angegeben. |
Beispielaufgabe 4
Untersuche die Funktion auf Extrempunkte.
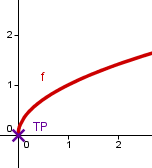
Beispiel | Allgemein |
|---|---|
Bestimmung und Nullsetzen der 1. Ableitung. Die 1. Ableitung hat keine Nullstellen. | |
Hat die Funktion also keine Extrema? | |
Doch, denn und der Definitionsbereich der Funktion ist auf einer Seite abgeschlossen. | |
| Betrachtung des Definitionsrandes. |
Man hat ein Extremum bei und es ist ein Minimum, da die Funktion dort wächst.
Übungsaufgaben
Laden
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zu den Extrempunkten
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
