Neben den regulären Extrempunkten müssen manchmal auch Randextrema bestimmt werden.
Diese treten auf, wenn es eine Eingrenzung der Definitionsmenge gibt. Dadurch erhält der Graph sogenannte Ränder, die ihn einschränken.
Hier lernst du unter anderem, wie du Randextrema berechnest. Diese musst du dann später auch bei der Ermittlung von absoluten und relativen Extrempunkten beachten.
Was sind Randextrempunkte?
Voraussetzung:
Die Definitionsmenge muss eingeschränkt sein.
Hierbei gibt es folgende Fälle:
eingeschlossene Ränder:
teils eingeschlossene Ränder: oder
ausgeschlossene Ränder:
Durch diesen eingeschränkten Definitionsbereich beschränkt man sich also auf einen Teilbereich des Graphen. Dadurch ergeben sich bis zu zwei weitere Punkte und an den Rändern, die sogenannten Randextrempunkte.
Graphische Darstellung
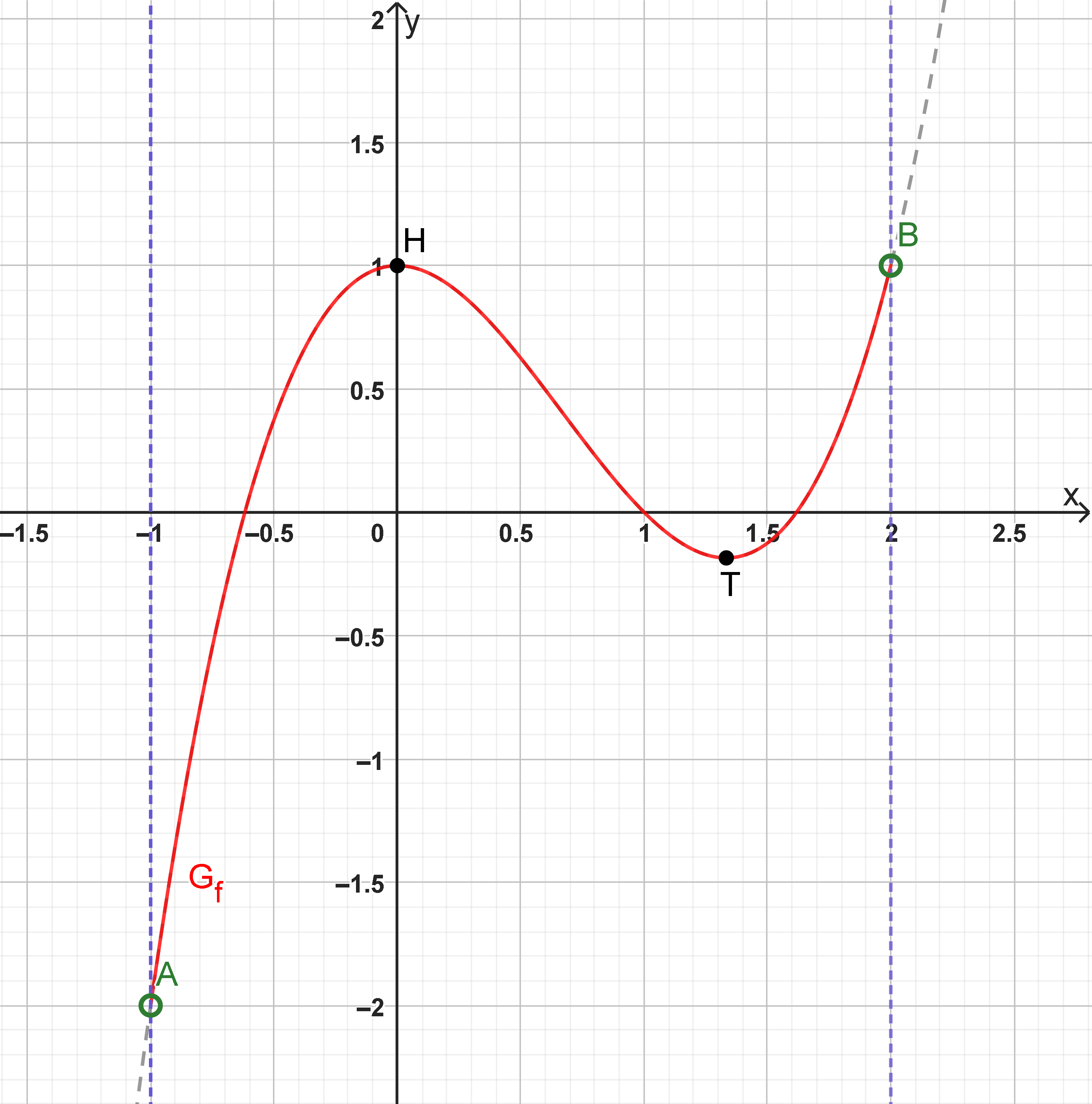
Bei der graphischen Darstellung wird ein eingeschlossener Randextrempunkt mit einem ausgefüllten Kreis ersichtlich. Die Darstellung eines ausgeschlossenen Punktes erfolgt mit einem leeren Kreis.
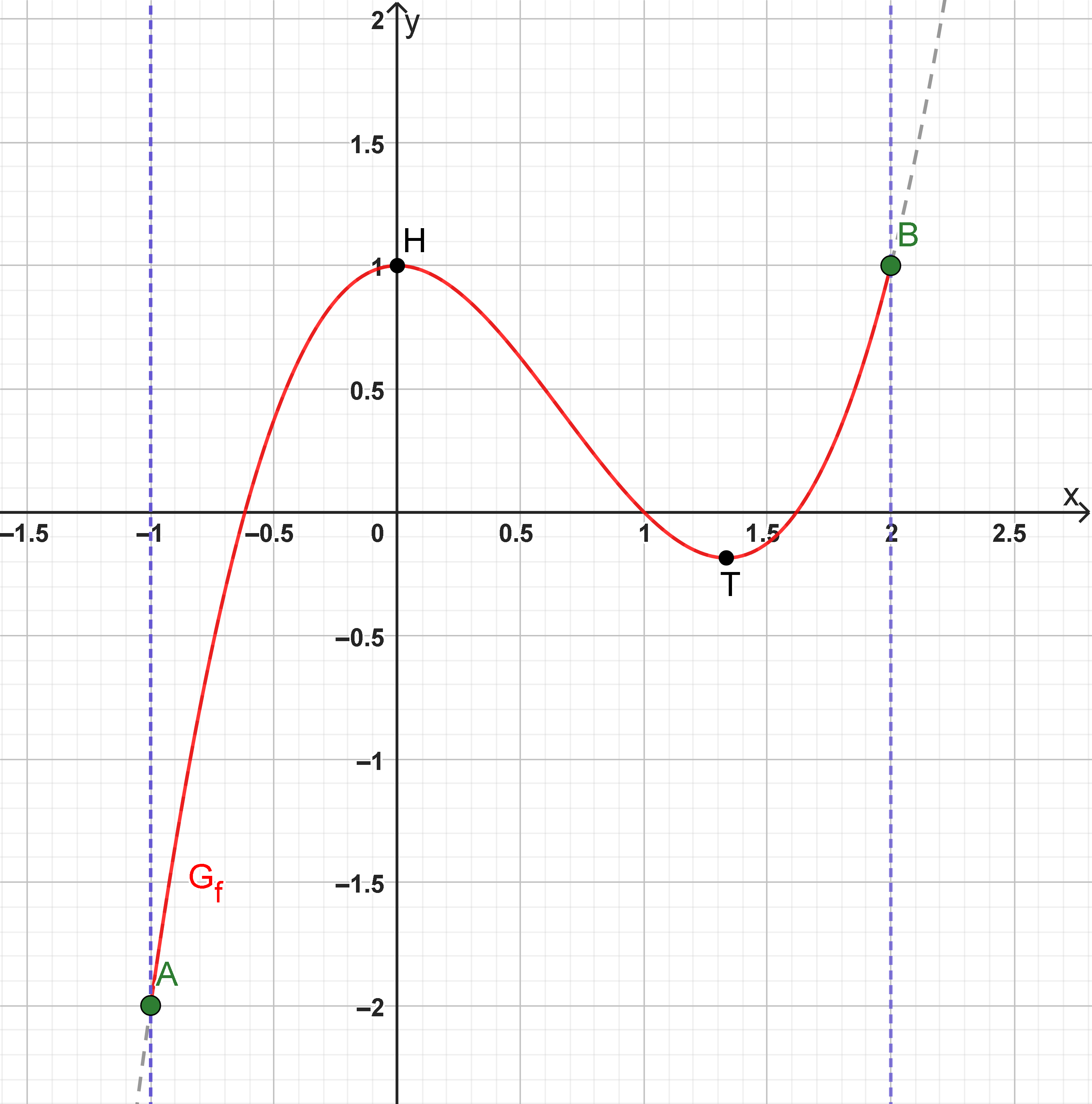
1. eingeschlossene Ränder
Hier siehst du einen Graphen, bei dem die Intervallgrenzen geschlossen bzw. die Ränder eingeschlossen sind.
Das erkennst du durch die ausgefüllten Kreise an den Punkten und .
Gegeben ist der Definitionsbereich:
Randextrempunkte:
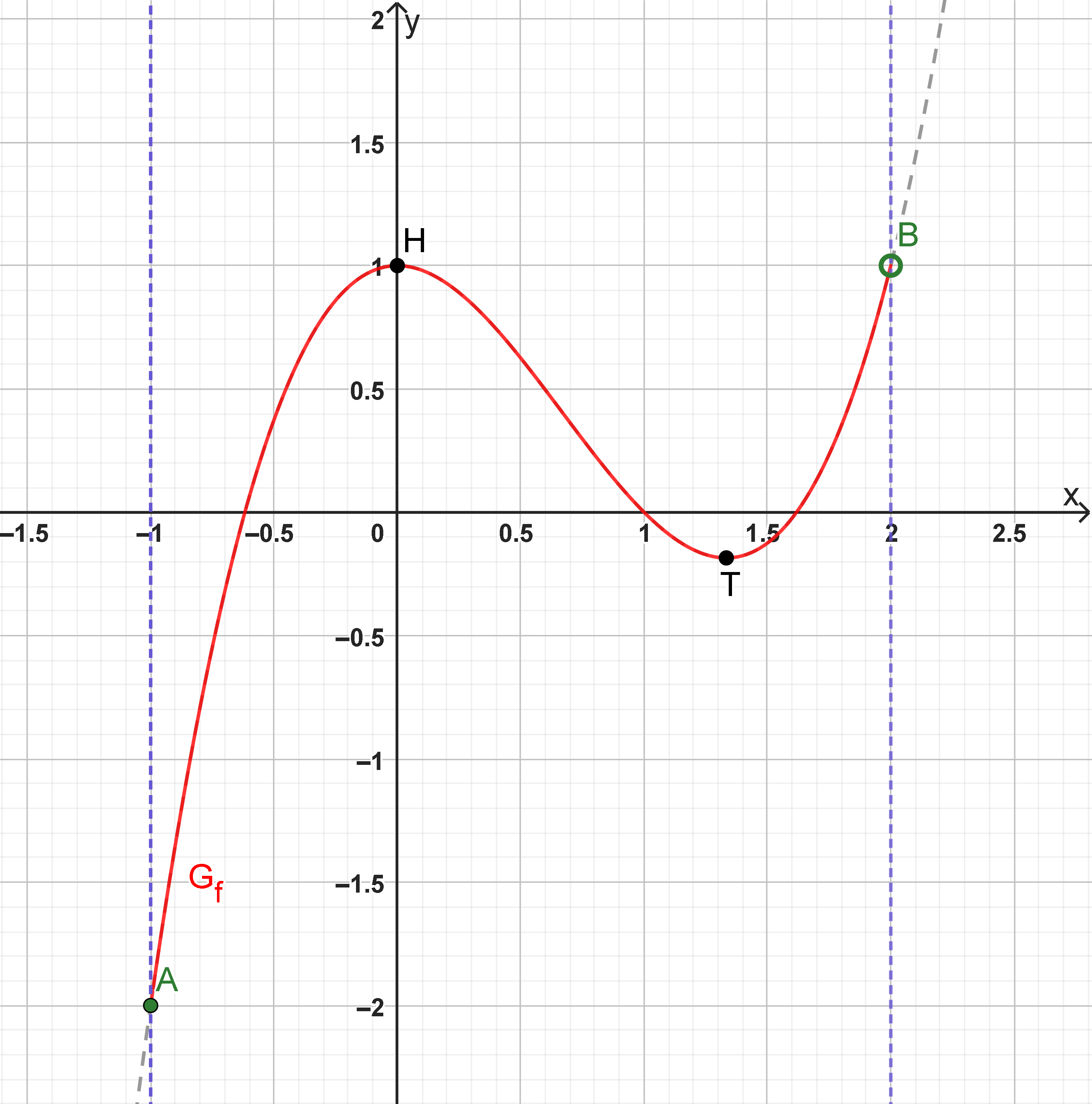
2. teils eingeschlossene Ränder
Hier siehst du einen Graphen, bei dem die Intervallgrenzen teils offen bzw. die Ränder teils eingeschlossen sind.
Das erkennst du durch den ausgefüllten Kreis am Punkt und an dem unausgefüllten Kreise am Punkt .
Gegeben ist der Definitionsbereich:
Randextrempunkte:
kein Randextrempunkt:
3. ausgeschlossene Ränder
Hier siehst du einen Graphen, bei dem die Intervallgrenzen offen bzw. die Ränder nicht eingeschlossen sind.
Das erkennst du durch die unausgefüllten Kreise an den Punkten und .
Gegeben ist der Definitionsbereich:
Keine Randextrempunkte: und