Die Betrachtung des Monotonieverhaltens einer Funktion ist fester Bestandteil der Kurvendiskussion.
Man bestimmt das Monotonieverhalten (bzw. die Monotonieintervalle) einer differenzierbaren Funktion über ihre erste Ableitung:
Wenn für alle -Werte in einem Bereich ist, ist die Funktion dort monoton steigend.
Wenn für alle -Werte in einem Bereich ist, ist die Funktion dort monoton fallend.

Berechnung des Monotonieverhaltens
Um herauszufinden, in welchen Bereichen der Graph monoton steigend oder monoton fallend ist, gibt es zwei Möglichkeiten:
Mit einer Monotonietabelle
Hier betrachtet man das Vorzeichen der 1. Ableitung um die Extrempunkte herum und schließt so auf das Monotonieverhalten.
Vorteil | Nachteil |
|---|---|
Man braucht nicht die 2. Ableitung. | Man muss die Polstellen berücksichtigen. (Eventuell braucht man die 1. Ableitung in einer faktorisierten Darstellung. Vergleiche dazu Linearfaktorzerlegung.) |
Mit der 2. Ableitung
Hier findet man zunächst heraus, ob Hochpunkte oder Tiefpunkte vorliegen und schließt dann auf das Monotonieverhalten.
Vorteil | Nachteil |
|---|---|
Man benötigt die 1. Ableitung nicht in einer faktorisierten Darstellung. | Man benötigt die 2. Ableitung. Diese kann mitunter sehr kompliziert werden. Bei manchen Funktionen benötigt man sogar die 3. Ableitung. Manchmal ermöglichen die Ableitungen auch gar keine Aussagen. |
Beispiel
Bestimme das Monotonieverhalten der Funktion
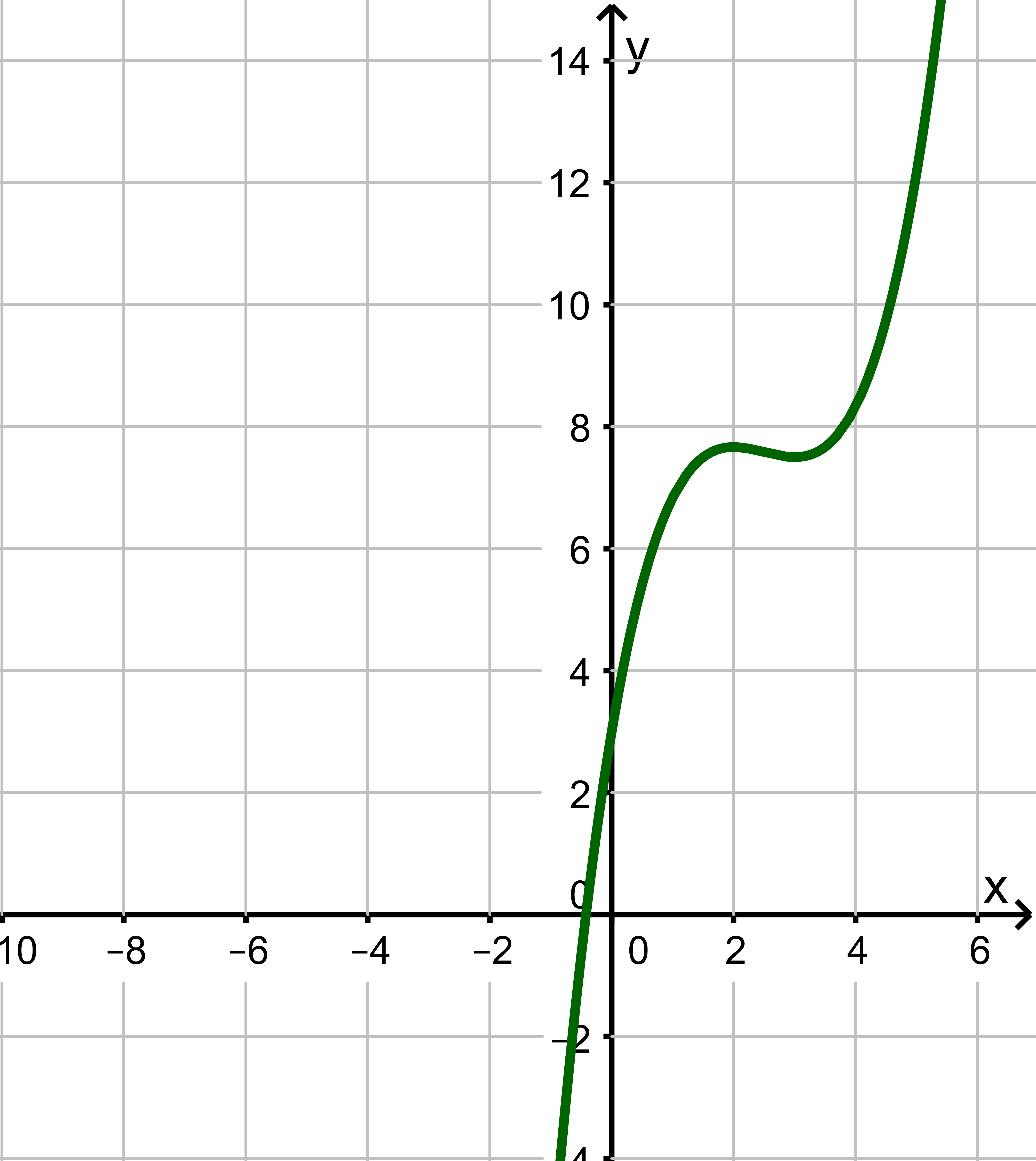
Mit einer Monotonietabelle
Bestimme die 1. Ableitung :
Erstelle nun eine Vorzeichentabelle:

Die waagrechte Linie versteht man als Zahlenstrahl. Dort werden der Größe nach die Nullstellen der 1. Ableitung angetragen (und evtl. die Polstellen der Ausgangsfunktion f(x); siehe "Achtung" unten).
Nun betrachtet man die Intervalle zwischen den angetragenen Nullstellen.
Man setzt irgendeinen Wert aus dem jeweiligen Intervall in die 1. Ableitung ein und notiert sich das Vorzeichen in die zweite Zeile.
Für das 1. Intervall wähle z.B. den Wert
Für das 2. Intervall wähle z.B. den Wert
Für das 3. Intervall wähle z.B. den Wert
Man kann die Vorzeichentabelle auch ausführlicher machen. Dazu benötigt man aber die 1. Ableitung in faktorisierter Darstellung:
Erstelle eine Vorzeichentabelle:

1) Zeile: Betrachte Werte für x, die kleiner als 2 sind. Dann ist das Vorzeichen des Faktors (x-2) ein Minus. Betrachtet man Werte zwischen 2 und 3 wird der Faktor (x-2) größer 0. Genauso für x-Werte, die größer als 3 sind.
2) Zeile: Gleiches Spiel in dieser Zeile nur das man den Faktor (x-3) betrachtet. Für Werte kleiner als 2 wird dieser Faktor natürlich negativ, genauso für Werte zwischen zwei und 3. Alle x-Werte die größer als 3 sind lassen den Faktor positiv werden.
Die Vorzeichen in der letzten Zeile ergeben sich aus der Multiplikation der Vorzeichen, die in einer Spalte darüber liegen.
Egal welche Variante der Vorzeichentabelle man verwendet, kann man nun die Monotonie des Graphen ablesen: Ist das Vorzeichen in der letzten Zeile ein so ist der Graph in diesem Bereich (inklusive die Ränder, außer die Ränder sind nicht im Definitionsbereich enthalten! Vergleiche hierzu: Monotonie) streng monoton steigend. Ist das Vorzeichen ein so ist der Graph in diesem Bereich streng monoton fallend:
streng monoton steigend
streng monoton fallend
Achtung: Wenn die Funktion eine oder mehrere Polstellen hat, müssen diese in der Vorzeichentabelle mit berücksichtigt werden. Man zeichnet dann einfach eine zusätzliche senkrechte Linie ein, die dann die Polstelle repräsentiert. Die Intervalle, die man dann betrachtet, werden somit von den Polstellen "zerstückelt".
Intervall | Monotonie |
|---|---|
ist streng monoton steigend im Intervall | |
ist streng monoton fallend im Intervall | |
ist streng monoton steigend im Intervall |
Mit der 2. Ableitung
Bestimme die 1. Ableitung
Bestimme die Nullstellen von :
| ↓ | Wende den Satz von Vieta oder die Mitternachtsformel an. | ||
und .
Bestimme die 2. Ableitung
Setze die Nullstellen der 1. Ableitung in die zweite Ableitung ein.
Betrachte folgende Fälle:
Fall | Folgerung |
|---|---|
Tiefpunkt im Punkt | |
Hochpunkt im Punkt | |
Bestimme die 3. Ableitung und setze die Nullstelle auch hier ein. Wenn Keine Aussage möglich. Wenn Terrassenpunkt und kein Monotoniewechsel |
Hochpunkt
Tiefpunkt
Wenn man weiß, ob ein Hoch-, Tief- oder Terrassenpunkt vorliegt, kennt man auch die Monotonie des Graphen vor bzw. nach diesen Stellen:
Tiefpunkt: links davon fallend, rechts davon steigend
Hochpunkt: links davon steigend, rechts davon fallend
Terrassenpunkt: links und rechts davon gleiche Monotonie
Hochpunkt bei und Tiefpunkt bei
Intervall | Monotonie |
|---|---|
ist streng monoton steigend im Intervall | |
ist streng monoton fallend im Intervall | |
ist streng monoton steigend im Intervall |
Übungsaufgaben
Laden
Weitere Aufgaben zum Thema findest du im folgenden Aufgabenordner:
Aufgaben zum Monotonieverhalten
