Betrag

Der Betrag einer Zahl ergibt sich als der Abstand der Zahl auf dem Zahlenstrahl von der Null. Man erhält ihn durch Weglassen des Vorzeichens. Falls eine Zahl positiv ist, ist der Betrag einfach diese Zahl. Falls die Zahl negativ ist, ist der Betrag das negative dieser Zahl. Die Schreibweise für den Betrag einer Zahl $x$ ist $\left|\mathbf x\right|$ .

Formal: Für eine Zahl $x$ ist $\def\arraystretch{1.25} \left|x\right|=\left\{\begin{array}{lc}\hphantom{-}x,&\text{falls}\;x\geq0\\-x,&\text{falls}\;x<0\end{array}\right.$

Eine Formel bzw. Variable in Betragsstrichen kann also nie negativ werden.

Zahlenstrahl

Verschiebe mit dem Regler den Wert zwischen $-5$ und $5$ .

Mit einem Klick auf Bild oder Button oben stimmst du zu, dass externe Inhalte von GeoGebra geladen werden. Dabei können persönliche Daten zu diesem Service übertragen werden – entsprechend unserer Datenschutzerklärung.

[https://www.geogebra.org/material/iframe/id/1551209]

Beispiele

Beträge von Zahlen:

\displaystyle \left|4\right|=4;\;\;\;\left|-4\right|=4;\;\;\;\left|-\frac14\right|=\frac14

Beträge in Termen:

\displaystyle \left|4\right|=4;\;\;\;\left|-4\right|=4;\;\;\;\left|-\frac14\right|=\frac14

\displaystyle \left|4\right|=4;\;\;\;\left|-4\right|=4;\;\;\;\left|-\frac14\right|=\frac14

\displaystyle \left|4\right|=4;\;\;\;\left|-4\right|=4;\;\;\;\left|-\frac14\right|=\frac14

Beträge in Funktionstermen:

$\def\arraystretch{1.25} f\left(x\right)=\left|x\right|+\left|x-1\right|-\left|x+3\right|=\left\{\begin{array}{ll}x+x-1-(x+3)&{x\geq1}\\x-(x-1)-(x+3)&0\leq x<1\\-x-(x-1)-(x+3) &-3\leq x<0\\-x-(x-1)-(-(x+3))&x<3\end{array}\right.$

Rechenregeln

Für alle Zahlen $x, y, z$ gelten folgende Regeln

$\left|x\right|\geq0$
$\left|x\cdot y\right|=\left|x\right|\cdot\left|y\right|$
$\left|x+y\right|\leq\left|x\right|+\left|y\right|$ (Dreiecksungleichung)

Auswirkungen auf die Kurvendiskussion

Beträge haben Auswirkungen auf viele Funktionseigenschaften:

Stetigkeit, Differenzierbarkeit, Wertemenge, Monotonieverhalten, Grenzwerte, Symmetrieverhalten.

Hier muss man die Funktion auf den einzeln definierten Abschnitten jeweils separat betrachten. Auf diesen Abschnitten ist die Funktion aber ohne Beträge definiert und kann "normal" behandelt werden.

Die Ableitung

Die Ableitung der Betragsfunktion ist für $x\neq0$ definiert als:

$\left|x\right|'=\frac x{\left|x\right|}$

Für $x=0$ ist der Betrag nicht differenzierbar:

Beweis

Untersuche die Funktion $f\left(x\right)=\left|x\right|=\begin{cases} x \text{ für } x\gt0\\0 \text{ für } x=0\\ -x\text{ für } x\lt0\end{cases}$ auf Differenzierbarkeit.

Diese Funktion ist offenbar für alle $x\in\mathbb{R}/\left\{0\right\}$ differenzierbar. Man muss also nur die kritische Stelle bei $x=0$ untersuchen.

Erstelle den Differentialquotienten an der Stelle $x_0=0$ .
Zunächst muss man unterscheiden, von welcher Seite man sich der $0$ annähert, da man für positive und negative Werte von $x$ unterschiedliche Funktionsterme verwenden muss. Man betrachtet also zwei Grenzwerte. Dabei nähert man sich einmal von links (in Zeichen: $\lim_{h\nearrow 0}$ ) und einmal von rechts (in Zeichen: $\lim_{h\searrow 0}$ ) an den Wert $x_0=0$ an.
2.1. Annäherung von rechts: $\lim\limits_{h\searrow 0}\frac{f(h)}{h}=\lim\limits_{h\searrow 0}\frac{h}{h}=\lim\limits_{h\searrow 0} 1=1$
2.2 Annäherung von links: $\lim\limits_{h\nearrow 0}\frac{f(h)}{h}=\lim\limits_{h\nearrow 0}\frac{-h}{h}=\lim\limits_{h\nearrow 0} -1=-1$

Da die beiden Grenzwerte von links und rechts unterschiedlich sind, existiert der Grenzwert an der Stelle $x_0=0$ nicht. Deshalb ist die Funktion $f\left(x\right)=\left|x\right|=\begin{cases} x \text{ für } x\gt0\\0 \text{ für } x=0\\ -x\text{ für } x\lt0\end{cases}$ an der Stelle $x_0=0$ nicht differenzierbar.

Die nicht differenzierbare Stelle $x = 0$ der Funktion $f(x)\;=\;\left|x\right|$ ist graphisch eine "Spitze".

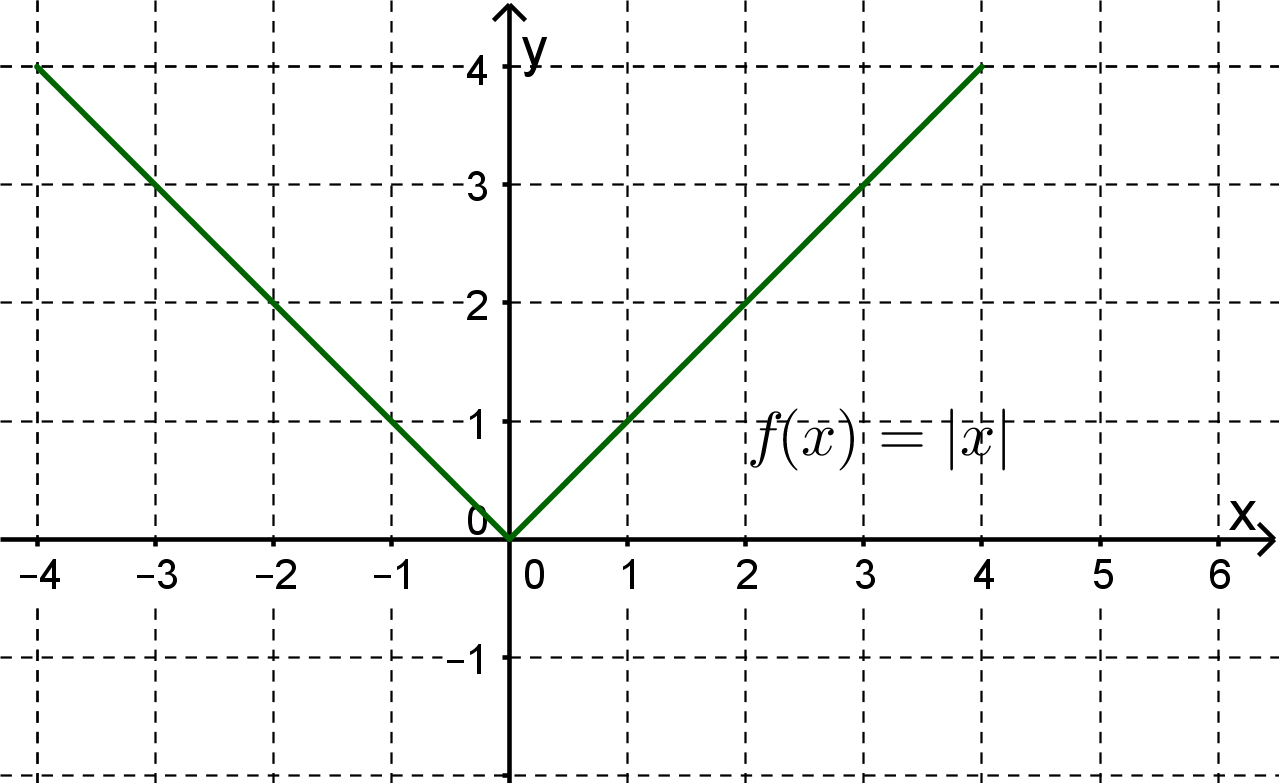
Beispiel

\displaystyle \left|4\right|=4;\;\;\;\left|-4\right|=4;\;\;\;\left|-\frac14\right|=\frac14

Es gelten alle Ableitungsregeln.

Zuerst wurde die äußere Potenz abgeleitet, danach der Betrag nachdifferenziert.

Da $x^2$ sowieso für $x$ und $-x$ die gleichen positiven Werte liefert, ist der Betrag hier überflüssig. Das zeigt auch die Ableitung, die identisch ist mit der Ableitung von $x^2$ .

Du hast noch nicht genug vom Thema?

Hier findest du noch weitere passende Inhalte zum Thema:

Videos

Betrag ganzer Zahlen

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?