Eine Funktion heißt genau dann stetig an einer Stelle , wenn der Funktionswert an dieser Stelle mit sowohl dem links- als auch rechtsseitigem Grenzwert identisch ist, d.h. wenn gilt:
Eine an allen Stellen des Definitionsbereichs stetige Funktion wird allgemein als stetig bezeichnet.
Umgekehrt nennt man eine Funktion unstetig, wenn obige Bedingung an mindestens einer Stelle ihres Definitionsbereichs nicht erfüllt ist.
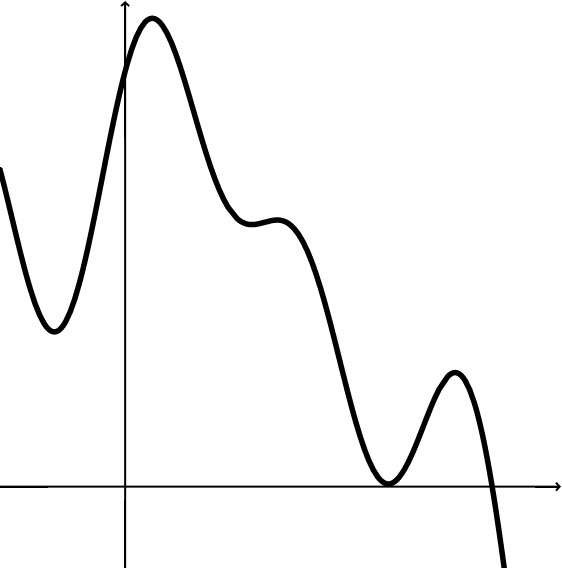
Anschauliche Darstellung
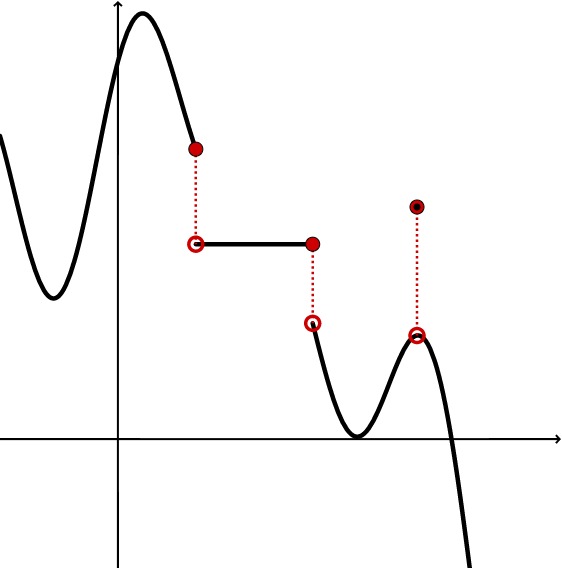
Eine stetige Funktion hat die Eigenschaft, dass ihr Graph an keiner Stelle einen Sprung macht. Du kannst den Graphen der Funktion also "in einem Zug, ohne Absetzen" zeichnen. Entsprechend besitzt eine unstetige Funktion sogenannte Unstetigkeitsstellen (z.B. Sprünge). Folgende Funktion ist beispielsweise unstetig:
Epsilon-Delta-Definition der Stetigkeit
Alternative Definition von Stetigkeit
Eine Funktion nennt man stetig im Punkt , wenn es für jedes ein gibt, sodass für alle gilt:
Ausführliche Erläuterung der Epsilon-Delta-Definition
Der Ausdruck ganz am Schluss bezeichnet den Abstand der Funktionswerte von und . Wir wollen, dass stetige Funktionen folgende Eigenschaft haben: Wenn uns jemand einen Abstand vorgibt, können wir einen Bereich um wählen, in dem der Abstand der Funktionswerte niemals größer als dieses wird. Diesen Bereich wählen wir symmetrisch um durch das Intervall . Wenn wir für jedes so eine Delta-Umgebung von x finden können, in der die Funktionswerte den -Abstand einhalten, dann ist die Funktion im Punkt stetig.
Übungsaufgaben
Laden
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
