Teilaufgabe a.)

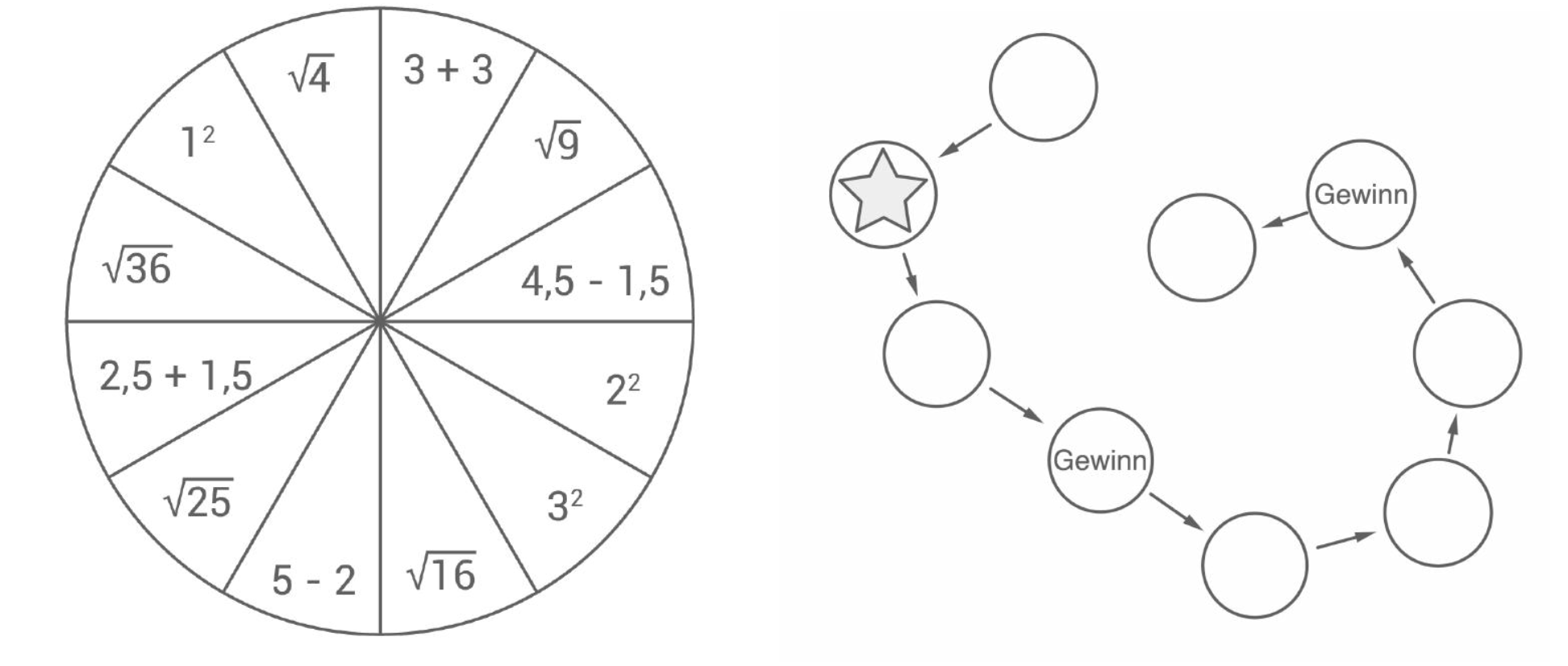
Berechnen aller Werte des Glücksrads.

$\sqrt{36}=61^2=1\sqrt{4}=23+3=6\sqrt{9}=3\mathrm{4,5}-\mathrm{1,5}=3$

$2^2=43^2=9\sqrt{16}=45-2=3\sqrt{25}=5\mathrm{2,5}+\mathrm{1,5}=4$

Berechnen der Wahrscheinlichkeit, einen Gewinn zu bekommen, wenn das Glücksrad ein Mal gedreht wird.

Um zu gewinnen muss Lisa die Spielfigur entweder $2$ oder $6$ Felder vorrücken.

Auf dem Glücksrad ist einmal eine $2$ und zweimal eine $6$, das sind $3$ von $12$ Ereignissen.

Die Wahrscheinlichkeit berechnet sich dann wie folgt:

${\mathrm{P}}_{\mathrm{G}\mathrm{e}\mathrm{w}\mathrm{i}\mathrm{n}\mathrm{n}}={\displaystyle \frac{3}{12}}={\displaystyle \frac{1}{4}}=25\%$

Die Wahrscheinlichkeit, dass Lisa gewinnt, beträgt $25\%$.

Teilaufgabe b.)

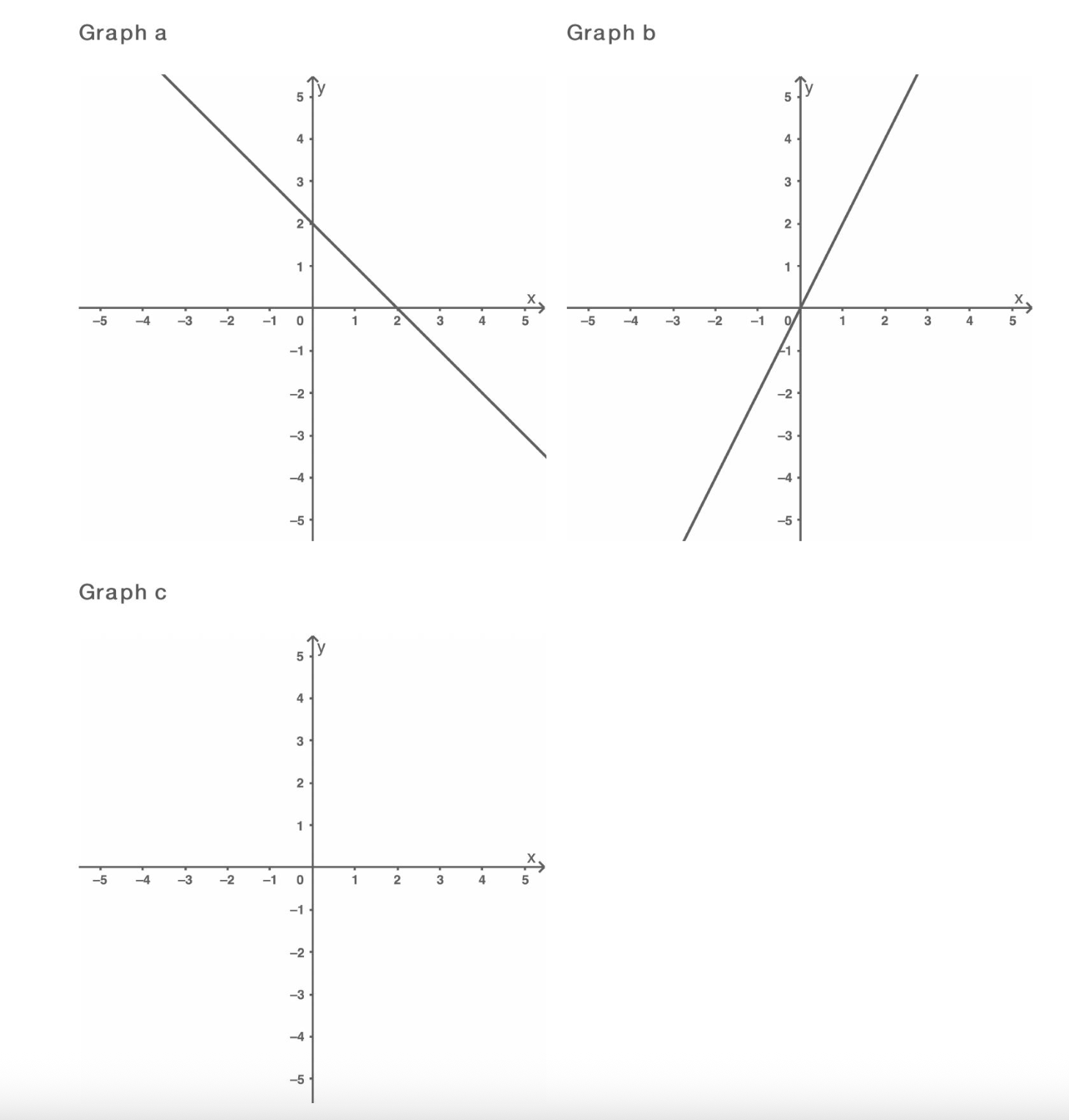
Ergänzen und zuordnen der Darstellungen:

Die allgemeine Geradengleichung lautet:

$\mathrm{y}=\mathrm{m}\cdot \mathrm{x}+\mathrm{t}$

Hier ist $\text{m}$ die Steigung der Geraden und $\text{t}$ der y-Wert, in dem die Gerade die y-Achse schneidet.

Die Wertetabelle 1 zeigt, dass der y-Wert gleich bleibt, der Graph ist eine Parallele zur x-Achse, welche die y-Achse bei $-3$ schneidet.

Der Graph sieht dann so aus:

Graph $\text{c}$ und Wertetabelle 1 gehören dann zur Funktionsgleichung $\text{𝐀}$.

Bei der Wertetabelle 2 erkennt man an dem Wertepaar $\left(0|0\right)$, dass die Gerade durch den Ursprung geht. Der y-Achsenabschnitt $\text{t}$ ist also null.

Graph $\text{b}$ ist eine Ursprungsgerade.

Aufstellen der Funktionsgleichung des Graphen b.

Da $\text{𝐭}$ gleich null ist, brauchen wir nur noch die Steigung $\text{𝐦}$ zu berechnen.

Die Formel zur Berechnung der Steigung einer Geraden lautet:

$\mathrm{m}={\displaystyle \frac{\mathrm{\Delta }\mathrm{y}}{\mathrm{\Delta }\mathrm{x}}}={\displaystyle \frac{{\mathrm{y}}_2-{\mathrm{y}}_1}{{\mathrm{x}}_2-{\mathrm{x}}_1}}$

Wir entnehmen der Wertetabelle 2 z. B. die Wertepaare $\left(1|2\right)$ und $\left(2|4\right)$, setzen sie in die Formel ein und berechnen die Steigung $\text{m}$.

$\mathrm{m}={\displaystyle \frac{4-2}{2-1}}\Rightarrow \mathrm{m}=2$

Die Funktionsgleichung $\text{C}$, lautet dann:

$\mathrm{y}=2\mathrm{x}$

Graph $\text{b}$ und Wertetabelle 2 gehören dann zur Funktionsgleichung $\text{𝐂}$.

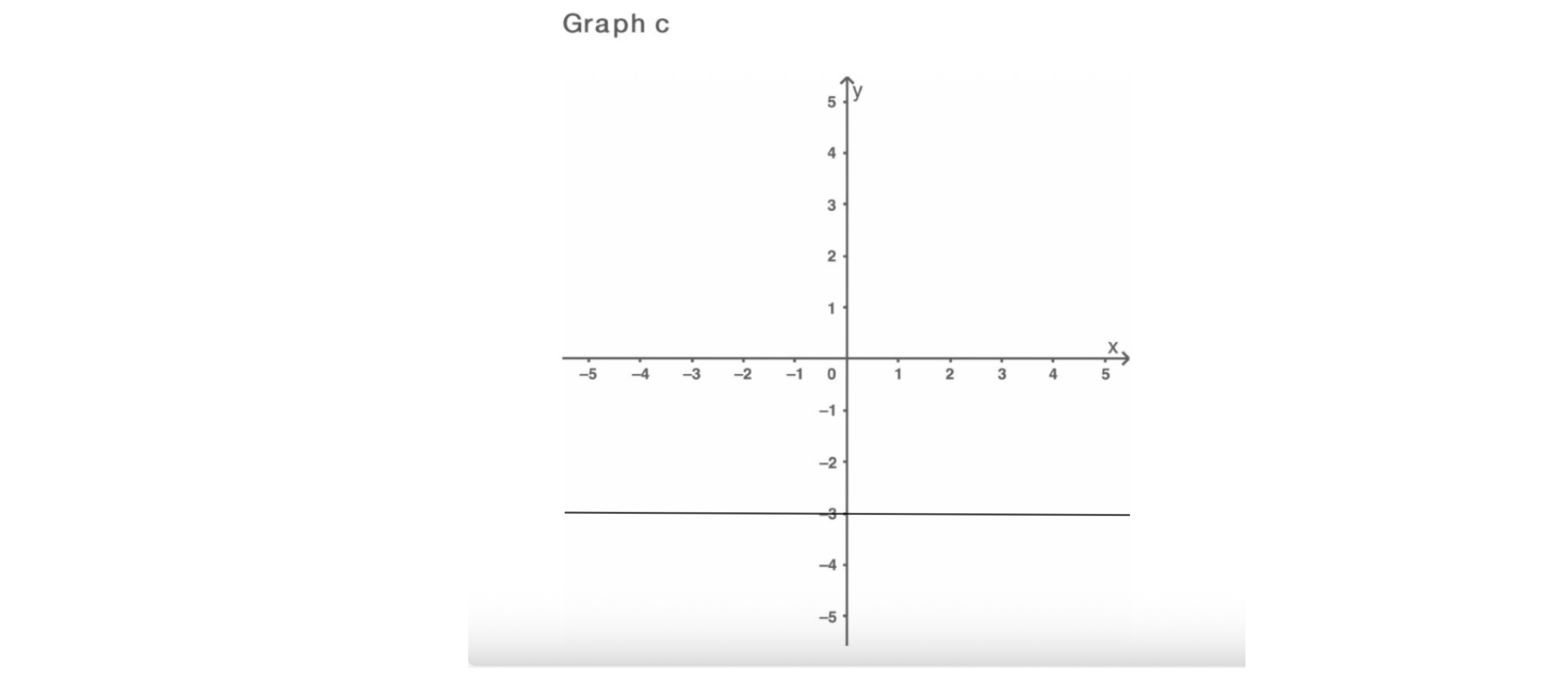
Wertetabelle 3 gehört zur Funktionsgleichung $\text{𝐁}$ und zu Graph $\text{a}$, wir ergänzen die Wertetabelle 3 entsprechend.

Zusammenfassung der Zuordnungen.