7. Ordnungsrelationen

Graphen

$\begin{array}{l}{E}_1=(K_1,K_3),E_2=(K_2,K_3),E_3=(K_2,K_4),E_4=(K_3,K_4),\\ K=\{K_1,K_2,K_3,K_4\},E=\{E_1,E_2,E_3,E_4\},\text{Graph }G=\{K,E\}.\end{array}$

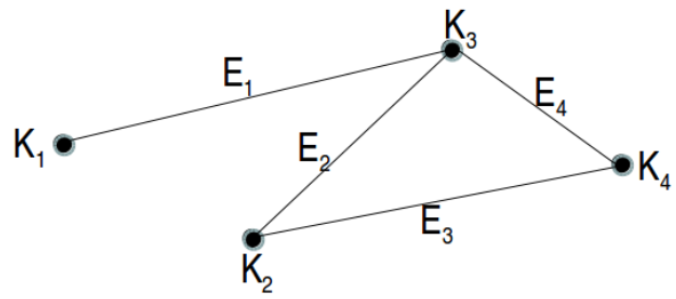
Spezielle Strukturen

• Liste

• Baum

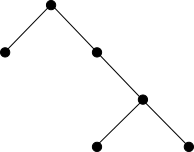
• Schleife/Kreise

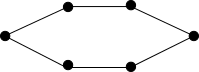
• Clique

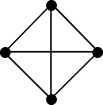
Eigenschaften von Relationen

Nun betrachten wir spezielle Relationen auf einer Menge $A$, um Ordnung (Struktur) in diese Menge zu bringen. Die Relationen werden dazu dienen, jeweils zwei Elemente zu vergleichen, etwa wie das $\le$ auf den reellen Zahlen.

• Transitiv: Wenn wir $x$ vor $y$ und $y$ vor $z$ einsortieren, sollte auch $x$ vor $z$ landen.

• Antisymmetrisch: Für zwei verschiedene Elemente $x\ne y$ wollen wir eine eindeutige Reihung haben, es darf nicht $xRy$ und $yRx$ sein.

• Reflexiv: Für $\le$ soll auch $xRx$ gelten. (Für $<$ gilt dies nicht)

Partielle Ordnung

Eine transitive, antisymmetrische und reflexive Relation heißt partielle Ordnung.

Beispiel

Warum "partiell", sieht man am besten an einem Beispiel:

Sei $A$ die Potenzmenge einer beliebigen Menge, z.B. $A=P\{\mathrm{1,2,3}\}$. Die Relation $\subseteq$ auf $A$, also "ist Teilmenge von", erfüllt die Bedingungen an eine partielle Ordnung. Wenn die Ausgangsmenge aber wenigstens zwei Elemente enthält, ist die Potenzmenge dadurch noch nicht geordnet, da z.B. weder $\{1\}\subseteq \{2\}$ noch $\{2\}\subseteq \{1\}$ gilt.

Die Relation sollte also auch noch konnex sein.

(Totale) Ordnung

Eine konnexe partielle Ordnung nennt man (totale) Ordnung.

In einer endlichen Menge $A$ mit einer totalen Ordnung $R$ kann man die Elemente so nummerieren ($A=\{x_1,x_2,\dots ,x_n\}$ mit $n=|A|$), dass gilt:

(oder anders ausgedrückt: $\forall i,j\in \{1,\dots ,n\}:i\le j\iff x_{i}R{x}_j$.

Beweis

Der Beweis ist konstruktiv. Wir geben einfach ein Verfahren (einen Algorithmus) an, das diese Ordnung herstellt (Quicksort).

Wir machen einen Induktionsbeweis nach $n$. Für $n=0$ und $n=1$ ist nichts zu zeigen, also sei nun $n>2$ und der Satz gelte für alle Mengen $B$ mit $0\le |B|\le n$.

Wir wählen ein beliebiges $z\in A$ (man nennt es Pivotelement) und zerlegen $A$ in drei Mengen:

• $A_1:=\{x\in A:xRz\wedge x\ne z\}$

• $A_2:=\{z\}$

• $A_3:=\{x\in A:zRx\wedge x\ne z\}$

Nun ist $A=A_1\cup A_2\cup A_3$, denn $R$ ist konnex: für jedes $x\in A$ gilt $xRz$ oder $zRx$ und somit

$\forall x\in A:(xRz\wedge x\ne z)\vee (x=z)\vee (zRx\ne z)$

Weiter sind die $A_i$ paarweise disjunkt: $A_1\cap A_2=A_1\cap A_3=A_2\cap A_3=\varnothing$ (Aufgabe: sortieren disjunkt).

Daher ist $|A|=|A_1|+1+|A_3|$, mithin $0\le |A_1|=:m<|A|$und $0\le |A_3|=n-1-m<|A|$. Wir wenden die Induktionsvoraussetzung an und nehmen an, dass $A_1=\{x_1,\dots ,x_m\}$ und $A_3=\{x_{m+2},\dots ,x_n\}$ sortiert sind (in $A_3$ sind die Indizes um $m+1$ verschoben, das stört die Sortierung nicht). Dann ist auch $A$ mit der Nummerierung $A=\{x_1,\dots ,x_m,x_{m+1}:=z,x_{m+2},\dots ,x_n\}$ sortiert.

Dieser Induktionsbeweis lässt sich in ein rekursives Programm umsetzen, in dem man zur Sortierung der Teilmengen $A_1$ und $A_3$ das Programm selbst wieder aufruft.

Für den Beweis ist die Effizienz der Konstruktion egal. Ein echtes Sortierverfahren in der Praxis sollte aber effizient (schnell) sein.