Zentrische Streckung (Konstruktion)

Die zentrische Streckung ist eine Ähnlichkeitsabbildung. Sie vergrößert oder verkleinert jede Strecke vom Streckzentrum $Z$ zu einem Punkt um den Streckfaktor $k$ .

Ist $| k | > 1$ wird die Strecke vergrößert. Ist $| k | < 1$ , wird die Strecke verkleinert.

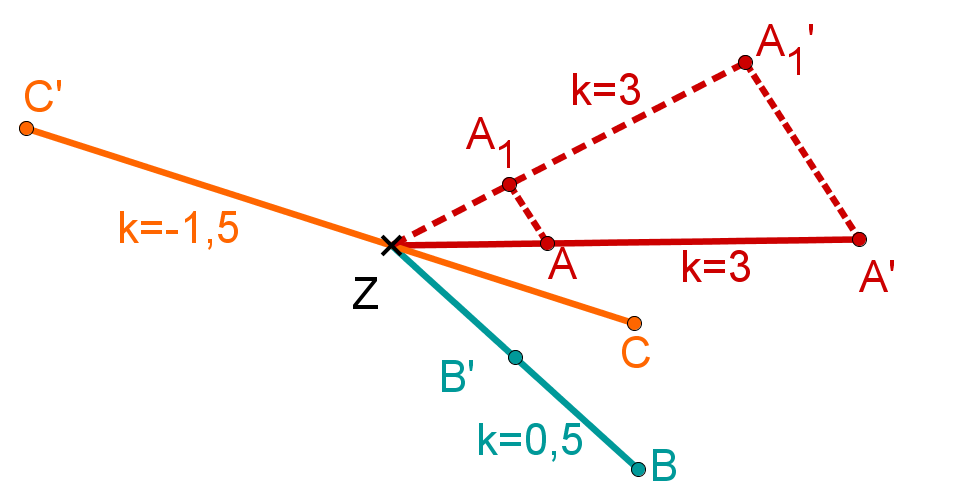
Zentrische Streckung durch Messen

Das Streckzentrum, welches mit $Z$ bezeichnet wird, gibt das Zentrum an, von dem aus die Streckung der Figur erfolgen soll. Der Streckfaktor $k$ gibt an, in welchem Verhältnis sich die Strecke verändert.

Im Folgenden wird dir die zentrische Streckung durch Abmessen anhand eines Beispiels näher erklärt. Nehmen wir mal an, wir haben das Dreieck ABC und wollen dieses vom Zentrum aus mit dem Streckfaktor $k$ zentrisch strecken.

Du hast also beispielsweise in einem Koordinatensystem dein Streckzentrum $Z$ bei $(1 | 1)$ .

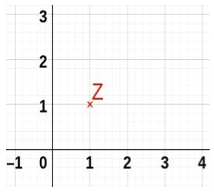
Nun hast du in deinem Koordinatensystem auch das Dreieck ABC mit den Punkten $A (2 | 2)$ , $B (2 | 5)$ und $C (5 | 3)$ gegeben.

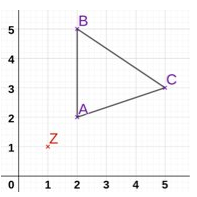
Jetzt misst du mit einem Lineal die Strecken zwischen dem Streckzentrum $Z$ und den Punkten A, B und C ab.

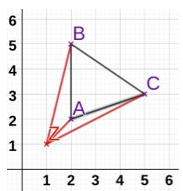
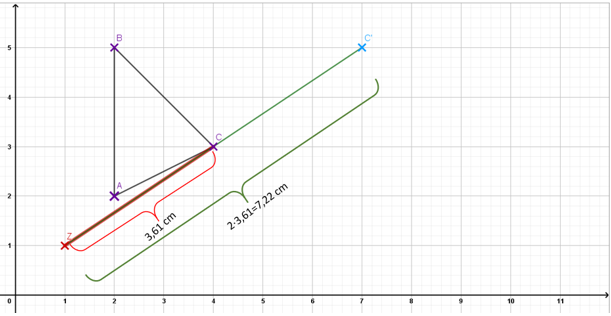
Dann multiplizierst du die abgemessene Strecke mit dem Streckfaktor $k = 2$ . Jetzt hast du deine Strecken zu den neuen Punkten und kannst diese bei $A^{'} (3 | 3)$ , $B^{'} (3 | 9)$ und $C^{'} (9 | 5)$ einzeichnen.

Zuletzt kannst du dann dein Dreieck A'B'C' einzeichnen. Und hast somit eine Abbildung deines ursprünglichen Dreiecks ABC.

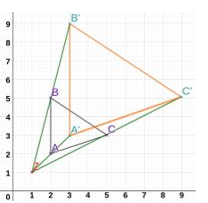
Zentrische Streckung mit Zirkel und Lineal

$A$ wird mit einem Streckfaktor $k = \frac{n}{m} \in ℚ$ (im Applet: $k = \frac{7}{5}$ , d.h. $n = 7$ und $m = 5$ ) auf der Geraden $g$ mit Zentrum $Z$ gestreckt.

Konstruiere eine beliebige Gerade $h$ , die durch das Zentrum $Z$ auf der Geraden g geht.
Zeichne dann einen Kreis mit Zirkel um $Z$ mit irgendeinem Radius $r$ .
Zeichne sechs weitere Kreise, mit dem selben Radius, dessen Mittelpunkt der Schnittpunkt des vorherigen Kreises mit der Geraden $h$ ist, sodass du insgesamt 7 Kreise hast, da du laut Beispiel einen Streckfaktor von $k = \frac{7}{5}$ .
Verbinde den $m$ -ten also den fünften Schnittpunkt (im Applet wird er mit "1" bezeichnet) mit $A$ .
Konstruiere eine Parallele von der Strecke [A1] durch den n-ten bzw. dem siebten Schnittpunkt.
Der Schnittpunkt dieser Parallelen mit der ursprünglichen Gerade $g$ ist der um $k = \frac{n}{m} = \frac{7}{5}$ gestreckte Bildpunkt $A^{'}$ von $A$ .

Hier findest du ein Applet, dass dir stufenweise die einzelnen Schritte grafisch erläutert. Ziehe hierfür mit deiner Maus, den Punkt den einzelnen Zahlen entlang, um die jeweiligen Etappen sehen zu können.

Laden

Beachte:

Ist $| k | < 1$ , also $n < m$ , dann muss man natürlich $m$ Kreise (und nicht nur $n$ ) zeichnen!
Für $k > 0$ : Der Punkt $A$ und sein Bildpunkt $A^{'}$ liegen auf der gleichen Seite bezüglich $Z$ .
Für $k < 0$ : Der Punkt $A$ und sein Bildpunkt $A^{'}$ liegen auf unterschiedlichen Seiten bezüglich $Z$ .
Für $| k | > 1$ : Die Strecke $Z A$ ist kleiner als die Strecke $Z A^{'}$ .
Für $| k | < 1$ : Die Strecke $Z A$ ist größer als die Strecke $Z A^{'}$ .

Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?