1 Übersicht
Dieser Kurs dient vor allem um einen Einstieg in das Thema „Teilchencharakter des Lichts“ zu finden und somit ist er auch ein guter Einstieg in die Quantenphysik. Der Fokus liegt dabei darauf, das Grundwissens aus den unteren Jahrgangsstufen knapp in Erinnerung zu rufen und einen Überblick über das Thema „Teilchencharakter des Lichts“ zu geben.
Inhalte
Wiederholung bisherige Kenntnisse über das Licht (Strahlen- und Wellenmodell)
Der photoelektrische Effekt und Einsteins Deutung
Photon (Impuls, Energie, Masse ...)
Ausblick in die Quantenphysik
Übungsaufgaben zum Festigen
Vorkenntnisse
Die nötigen Vorkenntnisse werden im Kurs wiederholt. Ist etwas noch unklar, so findest du die entsprechenden Artikel oder Themengebiete verlinkt, wo du dann dein Wissen vertiefen kannst.
<!---

-->

2 Wiederholung: Lichtstrahlen
Zur Erinnerung wiederholen wir knapp, was wir über das Licht bisher gelernt haben. Die Vorstellung, was Licht ist, hat sich in der Geschichte immer wieder geändert. Dabei gab es verschiedene Modelle die bestimmte Eigenschaften des Lichtes beschreiben. Es ist wichtig zu beachten, dass ein physikalisches Modell eben nur bestimmte Eigenschaften eines Naturphänomens erklärt und zum besseren Verständnis dient.
Lichtstrahlen
Lichtstrahlen sind ein einfaches Modell des Lichtes aus der Strahlenoptik (oder auch geometrische Optik genannt). Sie sind Halbgeraden, die von einer Lichtquelle ausgehen und sich geradlinig weiter ausbreiten. Lichtstrahlen sind hilfreich für die Beschreibung von Licht bei
der Reflexion
Brechung beim Übergang in andere Medien
Entstehung von Schatten
verhalten bei optischen Geräten und Bauelementen ( Spiegel, Linse, Mikroskop, Fernrohr, Prisma)

Abb. 1: Lichtstrahlen im Wald
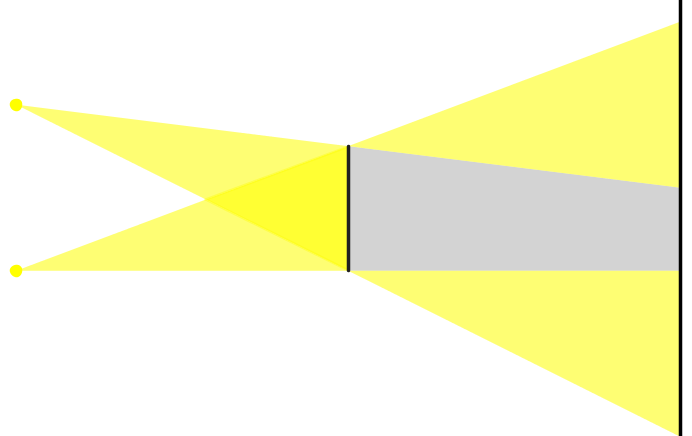
Abb. 2: Schattenbildung mit zwei Lichtquellen

Abb. 3: Lichtbrechung im Prisma

Abb. 4: Lichtbrechung im Wasser
Bereits hier in Abbildung 3 sehen wir, dass das Strahlenmodell bei der Beschreibung der Lichtbrechung im Prisma versagt, wenn wie die Farbunterschiede berücksichtigen wollen.
Quallenangaben:
Abb. 3: Von Spigget - Eigenes Werk, CC BY-SA 3.0, via Wikimedia Commons
Abb. 4: Von Rainald62 - Eigenes Werk, CC BY-SA 2.5, via Wikimedia Commons
3 Licht als Welle
Bestimmte Phänomene des Lichtes lassen sich nicht mit dem Modell der Lichtstrahlen erklären, weswegen die Erweiterung aus der Wellenoptik nötig ist. Diese unterliegen dem Huygensschen Prinzip, wo jeder Punkt einer Wellenfront Ausgangspunkt einer neuen Welle, auch Elementarwelle genannt, ist. Mit diesem Prinzip lassen sich folgende Phänomene besonders gut erklären.
Beugung
Interferenz
Polarisation des Lichtes
Zuordnung der Farbe des Licht einer Wellenlänge
Bekannte Experimente und Anwendungen sind:
Einfach- / Doppelspaltexperiment
Beugung am Gitter zur Spektralanalyse

Abb. 1: Interferenzfarben bei einem dünen Ölfilm auf Wasser
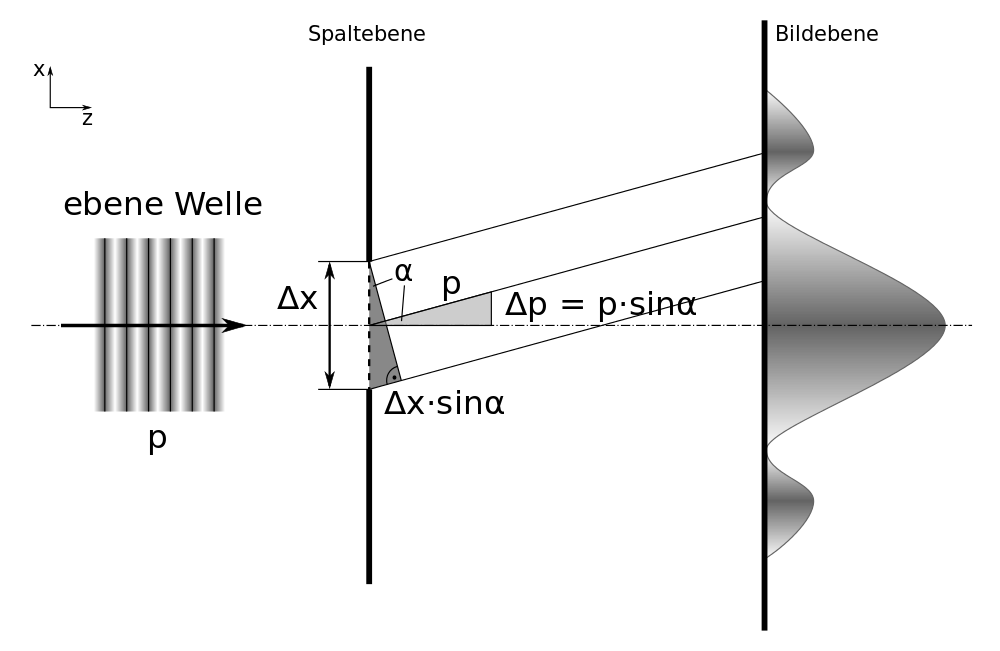
Abb. 2: Beugung am Einfachspalt (schematisch)
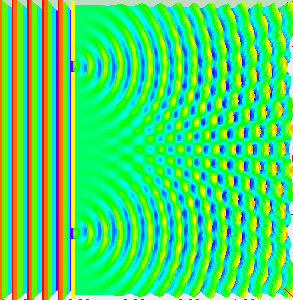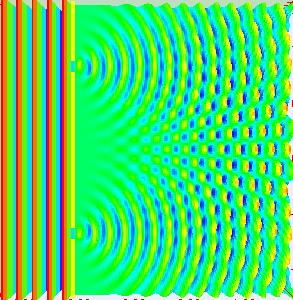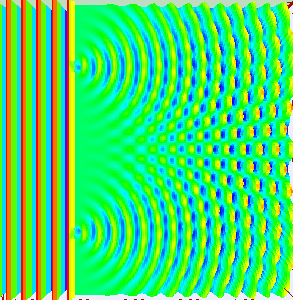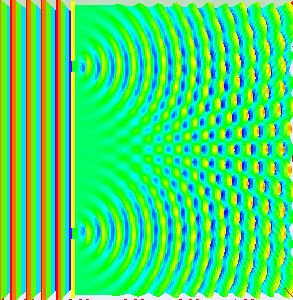
Abb. 3: Beugung einer ebenen Welle an einem Doppelspalt
Quallenangaben:
Abb. 1: Ausgeschnitten Von John - Eigenes Werk, CC BY-SA 3.0, via Wikimedia Commons
Abb. 3: Von Lookang - Eigenes Werk, CC BY-SA 3.0, via Wikimedia Commons
4 Elektromagnetische Wellen
Nachdem Maxwell seine Grundgleichungen für die Elektrodynamik formuliert hatte, erkannte er, dass sich elektromagnetische Wellen, ebenso wie Licht, mit Lichtgeschwindigkeit bewegen. Aus dieser Erkenntnis hat er seine Folgerung, dass das Licht ebenfalls eine elektromagnetische Welle ist, gezogen.
Bei Licht handelt es sich um den sichtbaren Teil (der Bereich der Wellenlängen von etwa 380 nm bis 780 nm) des elektromagnetischen Spektrums.
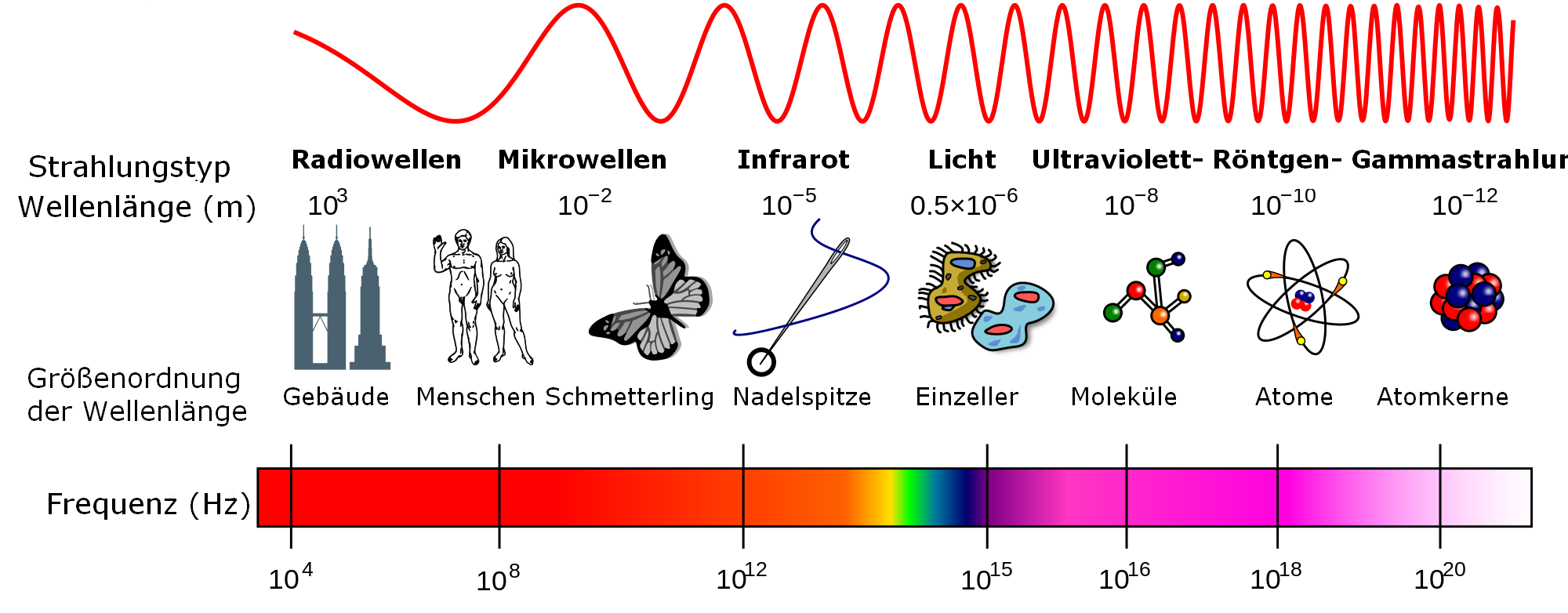
Abb. 1: Das elektromagnetisches Spektrum
Quallenangaben:
Abb. 1: Ausgeschnitten von HolgerFiedler - Bearbeter Werk, CC BY-SA 3.0, via Wikimedia Commons
5 Äußerer photoelektrischer Effekt (Hallwachs-Effekt)
Bereits ab dem 19. Jahrhundert entdeckten einige Physiker, dass Elektronen mit Hilfe von Licht aus einer Metalloberfläche herausgelöst werden können. So konnten z. B. Heinrich Hertz und Wilhelm Hallwachs diesen Entladevorgang eines Metalls, auch bekannt als Hallwachs-Effekt, demonstrieren. Dabei stellten sie auch fest, dass für den Versuch ultraviolettes Licht, jedoch kein sichtbares Licht, geeignet ist.
Dieser Effekt konnte lange nicht erklärt werden. Es war Albert Einstein, der diesen als erster richtig deuten konnte und u.a. auch deshalb einen Nobelpreis erhielt.
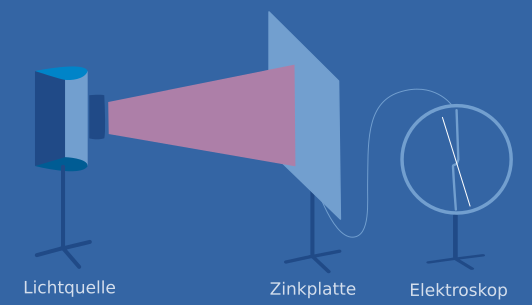
Versuchsaufbau
Eine Zinkplatte, die sowohl positiv als auch negativ geladen werden kann, ist mit einem Elektroskop verbunden. An diesem kann die momentane Ladung der Platte abgelesen werden.
Durchführung
Die Platte wird jeweils unterschiedlich geladen und mit Licht verschiedener Frequenzen ( Gelb, Grün, Blau, UV) bestrahlt.
Beobachtung
Wenn die Platte positiv geladen ist, ist keine Veränderung zu sehen.
Ebenso wenig passiert, wenn die negativ geladene Platte mit gelbem, grünem, blauem Licht bestrahlt wird.
Ist jedoch die Platte negativ geladen und wird mit UV-Licht (hohe Frequenz) bestrahlt, so wird die Platte entladen.
Zusätzlich kann man beobachten, dass sich die Grenzwellenlänge bzw. Frequenz, bei der der Effekt erstmals auftritt, ändert. Grenzwellenlänge bzw. Frequenz sind dabei abhängig vom benutzten Metall.
Folgerung
Wir schließen daraus, dass Licht (mit bestimmter Wellenlänge) den Austritt der Elektronen hervorruft. Im Falle der Zinkplatte geschieht dies erst im UV-Bereich.
Das Experiment mit der Zinkplatte bildet jedoch erst den Anfang. Mit der Zeit wurden weitere Experimente entworfen und durchgeführt, um den Photoeffekt näher zu untersuchen. Mehr dazu im Artikel: photoelektrischer Effekt
So ist man in der Lage, die Geschwindigkeit der Elektronen nach ihrem Austritt zu bestimmen, z. B. mit Hilfe der Gegenfeldmethode.
Energie des homogenen elektrischen Feldes
Kinetische Energie des Elektrons
Diese Energien müssen gleich groß sein. Man erhält somit:
6 Einsteins Deutung
Zuerst soll betrachtet werden, was man nach der klassischen Vorstellung erwarten würde und welche Widersprüche sich im Versuch ergaben.
Widersprüche zur klassischen Erwartung
Ausgehend vom Wellencharachter des Lichts würde man folgendes erwarten:
Erwartung | Beobachtung |
|---|---|
Energie abhängig von der Amplitude (Intensität) des Lichts | Abhängig von der Wellenlänge |
Kontinuierliche Aufnahme der Energie und zeitliche Verzögerung bis zum Auftreten des Effekts | Photoeffekt ist instantan (augenblicklich) |
Lichtquanten
Anstatt Licht nur als Welle zu betrachten, geht Einstein von sogenannten Lichtquanten aus. Diese Lichtquanten enthalten die Energie des Lichtes und sind zählbar, bewegen sich, ohne sich zu teilen, und können nur als Ganzes absorbiert werden.
Zudem ist die Energie des Quants abhängig von der Wellenlänge und alle Lichtquanten der gleichen Wellenlänge besitzen die gleiche Energie.
Ein Elektron kann somit nicht jeden möglichen Energiebetrag aufnehmen, sondern lediglich ein Lichtquant absorbieren und dessen gesamte Energie aufnehmen oder kein Lichtquant aufnehmen und damit auch keine Energie.
Später wurde die Bezeichnung Lichtquant durch den Begriff des Photons ersetzt.
Für den Versuch gilt:
Wellenlänge * Grenzwellenlänge | Energie unzureichend |
|---|---|
Wellenlänge Grenzwellenlänge | Elektronen werden gelöst |
* kleine Wellenlänge bedeutet eine größere Frequenz, was einer höheren Energie entspricht
Bei höherer Intensität werden mehr Elektronen pro Zeiteinheit emittiert, was zu einem höheren Photostrom, aber nicht zu höherer Spannung (Energie der Elektronen) führt.
7 Zusammenfassung
Wir haben einige Modelle des Lichts kennengelernt, die sich zur Beschreibung bestimmter Phänomene gut eignen. Neu dazu gekommen ist, dass Licht als Teilchen auftreten kann.
Modell | Eigenschaften | Beschreibt |
|---|---|---|
Lichtstrahlen | Breiten sich im Raum geradlinig aus | Reflexion, Brechung, Schatten, Verhalten bei optischen Geräten… |
Lichtwellen | Wellen, die dem Huygensschen Prinzip unterliegen | Beugung, Interferenz, Polarisation… |
Lichtquanten | Unteilbare, zählbare Teilchen, die die Energie des Lichts enthalten | Photoeffekt, quantenphysikalische Phänomene |
Äußerer Photoeffekt
Mit Hilfe von Lichtstrahlen lassen sich Elektronen aus einer Metalloberfläche herauslösen. Wir haben einige Experimente zur Demonstration des Effekts kennengelernt. Wichtige Erkenntnise bzw. Beobachtungen waren
Eine negativ geladen Zinkplatte wird mit UV-Licht (hohe Frequenz) bestrahlt und die Platte entlädt sich.
Die Energie der Elektronen ist abhängig von der Wellenlänge des Lichts aber nicht von der Intensität
Ein Elektron kann nicht kontinuierlich jeden möglichen Energiebetrag aufnehmen, sondern lediglich ein Photon (Lichtquant) absorbieren und dessen gesamte Energie aufnehmen oder kein Photon aufnehmen und damit auch keine Energie. (Quantelung der Energie)
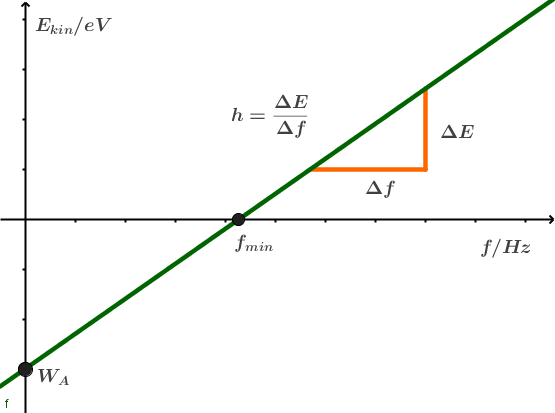
Mit Hilfe der Gegenfeldmethode gilt für die Energie der Elektronen folgender Zusammenhang:
beschreibt somit den Zusammenhang von Frequenz und der Energie eines Photons.
8 Aufgaben
TBD
9 Photonen
Ausgehend von Einsteins Deutung zum Photoeffekt wurde der Begriff Photon eingeführt. Wir halten hier einige wichtige Eigenschaften des Photons fest.
Energie
Ein Photon ist das Elementarteilchen des Lichts. Sie sind kleine, nicht teilbare Energiequanten (Energiepakete). Das heißt: Es gibt keine 1,5 Photonen oder 3,7 Photonen sondern immer nur 1, 2, 3,… 100, … also nur eine ganzzahlige Anzahl von Energiequanten.Für die Energie eines Photons gilt:
Das bedeutet auch, dass die Energie nicht kontinuierlich über dem Raum verteilt ist. Mehrere solcher Energiepakete breiten sich im Raum aus.
Geschwindigkeit
Photonen bewegen sich stets mit der Lichtgeschwindigkeit c.
Masse
Ein Photon besitzt keine Ruhemasse jedoch aber eine relativistische Masse nach .
Impuls
Mit der relativistischen Masse besitzt ein Photon auch einen relativistischen Impuls.
10 Compton-Effekt
Der Compton-Effekt dient als wichtiger Nachweis der Teilcheneigenschaften von Photonen. Es handelt sich dabei um das Phänomen, dass elektromagnetische Strahlung seine Wellenlänge bei Streuung an Elektronen ändert.
Experimenteller Aufbau und Ablauf
A.H. Compton führte seine Experimente mit Röntgenstrahlung und Graphit durch. Dazu bestrahlte er einen Streukörper aus Graphit mit Röntgenstrahlen einer bekannten Wellenlänge und maß die Wellenlänge der gestreuten Strahlung in Abhängigkeit des Streuwinkels .
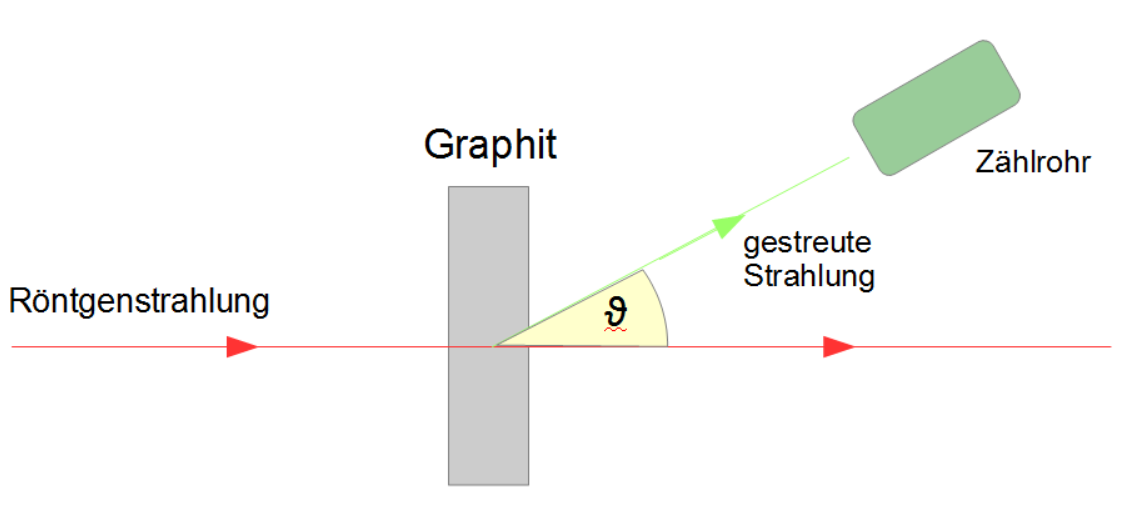
Abbildung 1: Schematischer Aufbau zur Beobachtung des Compton-Effekts
Beobachtungen
Streustrahlung beinhaltet ursprüngliche Wellenlänge und eine neue Wellenlänge .
Die neue Wellenlänge ist größer als die ursprüngliche Wellenlänge, die Frequenz kleiner.
Je größer der Streuwinkel , desto größer der Wellenlängenunterschied
unabhängig von der Wellenlänge der Ausgangstrahlung, ausschleßlich von abhängig
unabhänigig vom Streukörper
Erklärung
Wir behalten im Hinterkopf, dass die Energie eines Photons gleich ist.
Warum verschiedene Wellenlängen?
Das Photon stößt gegen ein Atom bzw. den Kern. Das ist ähnlich wie ein Tennisball der gegen eine Wand geworfen wird. Da die Wand fest ist und keine Energie vom Tennisball aufnimmt kommt der Ball mit nahezu gleicher Geschwindigkeit (Energie) wieder zurück. Bei unserem Versuch würde sich die Wellenlänge nicht ändern sondern nur die Richtung des Photons.
Stößt jedoch das Photon gegen ein Elektron (das sich frei bewegt) so findet ein zweidimensionaler elastischer Stoß statt. Der Photon wird ebenfalls hier abgelenkt besitzt jedoch weniger Energie da ein Teil der Energie nach der Energieerhaltung an das Elektron abgegeben wird.Nun betrachten wir jedoch unsere Formel und bedenken dass sowohl h und die Lichtgeschwindigkeit sich nicht ändern. Ein Photon (Licht) kann nicht langsamer oder schneller werden. Daher muss sich die Wellenlänge des Photons ändern, genauer gesagt kleiner werden.
Compton leitete für diesen Zusammenhang seine Formel
her. Dabei ist die sogenannte Comptonwellenlänge (für Elektronen).
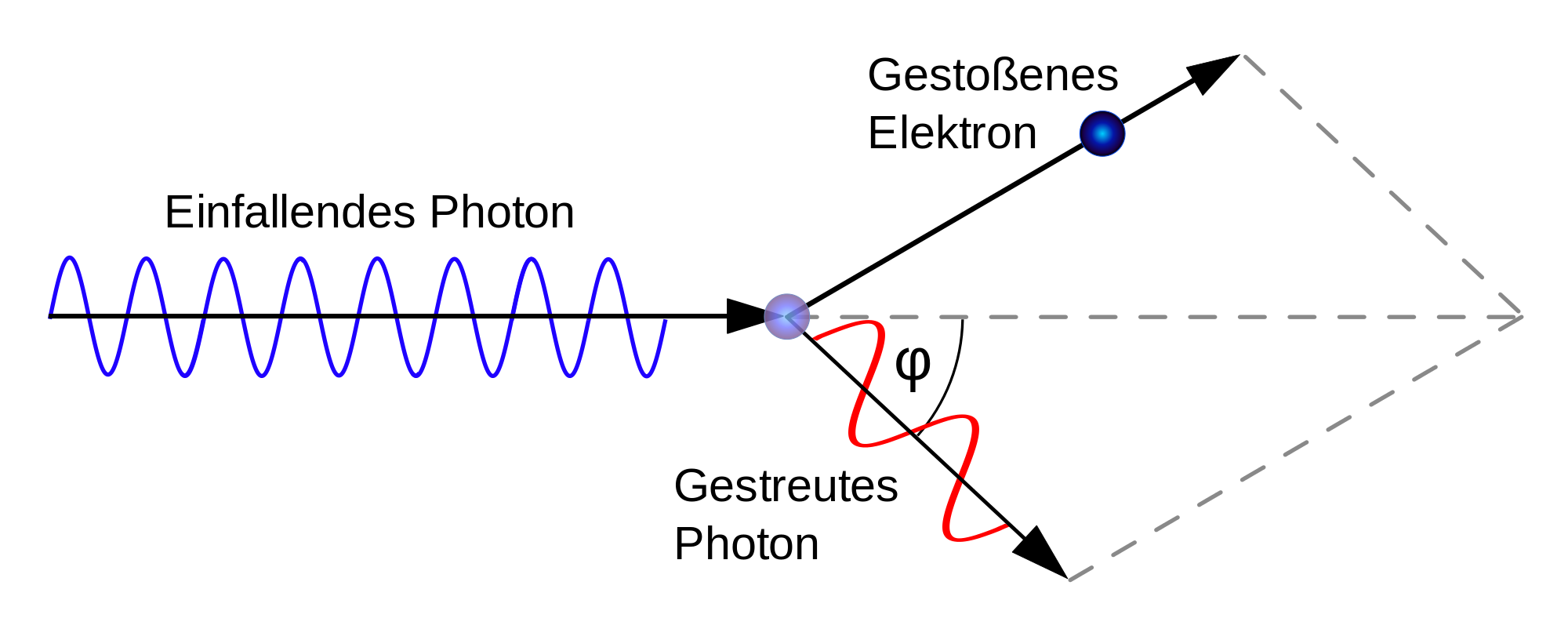
Abbildung 2: Stoßprozess zwischen Photon und Elektron
Diese Formel zeigt deutlich, dass der Wellenlängenunterschied ausschließlich vom Streuwinkel und nicht von anderen Faktoren wie der ursprünglichen Wellenlänge abhängt.
Quellenangabe
Abb. 1: eigene Grafik
Abb. 2: By EoD (Own work) GFDL, CC-BY-SA-3.0, CC BY-SA 2.5-2.0-1.0 via Wikimedia Commons
11 Ist Licht nun ein Teilchen?
Die Antwort auf die Frage lautet sowohl Ja als auch Nein!
Genauer gesagt haben wir die Frage bereit beantwortet. Es kommt darauf an was man betrachtet. Sowohl Licht als Strahl, Welle oder Teilchen sind Modelle. Modelle eignen sich immer um bestimmte physikalische Eigenschaften zu beschreiben.
Das Strahlenmodell ist hilfreich um Licht auf größere Entfernungen zu beschreiben. Dabei lassen sich Schatten, Reflexion, Brechung bei größeren Entfernungen gut darstellen usw. …
Betrachten wir das Licht nicht mehr auf größere Entfernung und wollen Phänomene wie Beugung oder Interferenz berücksichtigen so ist das Wellenmodell sehr gut geeignet.
Im Endeffekt haben wir gesagt das Licht eine elektromagnetische Welle ist bis der Teilchencharakter der Lichts bekannt wurde.
Quantenobjekt
Der Photoeffekt war ausschlaggebend für die Quantenphysik. In der Quantenphysik werden wir den Begriff Quantenobjekte kennenlernen. Zum Beispiel ist Licht ein Quantenobjekt. Quantenobjekte haben sowohl die Eigenschaft einer Welle als auch eines Teilchen. Die Antwort ist nicht mehr entweder Welle oder Teilchen sondern beides. Mehr dazu findet du unter Welle-Teilchen Dualismus.
Ausblick
Auch Elektronen zählen zu den Quantenobjekten. Elektronen mit Welleneigenschaften? Mehr dazu erfährst du im Themenbereich Wellencharakter des Elektrons.