6Lösung 3a

Aufgabenstellung

$3$Eine dritte Modellierung des Querschnitts der Tunnelwand, bei der ebenfalls die Bedingungen I und II erfüllt sind, verwendet die Funktion $f: x\mapsto \sqrt{25-x^2}$ mit Definitionsbereich $D_f=[-5;5]$.

Begründen Sie, dass in diesem Modell jeder Punkt des Querschnitts der Tunnelwand von der Bodenmitte M den Abstand $5 m$ hat. Zeichnen Sie den Graphen von f in ein Koordinatensystem ein (Platzbedarf im Hinblick auf spätere Aufgaben: $5\le x\le 9$, $1\le y\le 13$) und begründen Sie, dass bei dieser Modellierung auch Bedingung III erfüllt ist. (5 BE)

Lösung

Jeder Punkt hat den Abstand $5m$ zur Bodenmitte

Den Abstand kann man ähnlich wie bei 1b über den Satz des Pythagoras berechnen.

$\def\arraystretch{1.25} \begin{array}{rl} q(x)^2&=&x^2+f(x)^2\\q(x)&=&\sqrt{x^2+(\sqrt{25-x^2})^2}\\&=&\sqrt{x^2+25-x^2}\\&=&\sqrt{25}=5\end{array}$

Damit hat man ausgerechnet, dass der Abstand von Punkt zur Bodenmitte immer $5m$ beträgt.

Graph in Koordinatensystem zeichnen

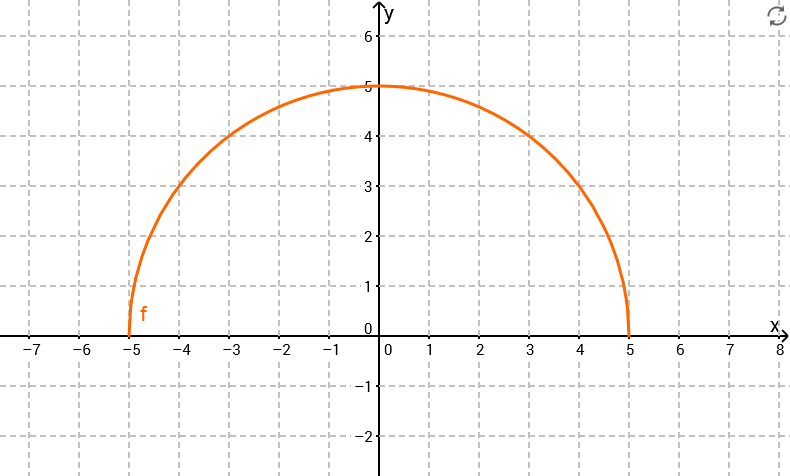
Bedingung III ist erfüllt

Gehe dazu vor wie bei Aufgabe 2b.

$f(3)=\sqrt{25-3^2}=\sqrt{16}=4$

Die Funktion ist, wie man an dem Graphen sieht, punktsymmetrisch. An der Stelle $x=3$ ist noch mind. $4m$ hoch, damit auch an der Stelle $x=-3$ und erfüllt damit die Bedingung III.