1 Übersicht
In diesem Kurs arbeitest du mit Open Roberta und dem Online-Simulator. Immer wenn du den Roboter hier rechts siehst, kannst du etwas direkt im Simulator testen

Den Simulator findest du auf folgender Webseite, klicke dort dann auf Open Roberta Sim:
https://lab.open-roberta.org/ (Klickst du mit der rechten Maustaste auf den Link, kannst du ihn in einem neuen Tab/Fenster öffnen)
Inhalt des Kurses
Ziel dieses Kurses ist es, mit Hilfe des Open Roberta Simulators den Roboter einen Kreis mit einem Radius von exakt fahren zu lassen.Benutze für diesen Kurs die Karte des Simulators, auf welcher ein Koordinatensystem abgebildet ist. Du siehst diese hier rechts.
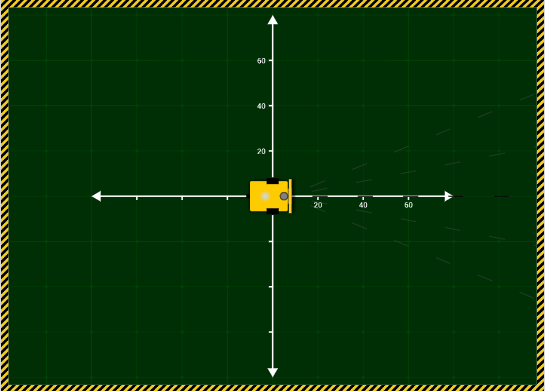
Voraussetzungen
Du solltest dich bereits mit dem Kreisumfang und der Berechnung von Geschwindigkeiten auskennen.
Dauer
Die Dauer dieses Kurses beträgt in etwa 40 min
2 Der Roboter
Der Roboter des Simulators ist wie auf dem Bild zu sehen aufgebaut:
Der Roboter wird mit zwei Motoren, an denen links und rechts die Räder angebracht sind, angetrieben. Diese Räder können jedoch nicht einlenken, wie du es vielleicht von einem Auto kennst.
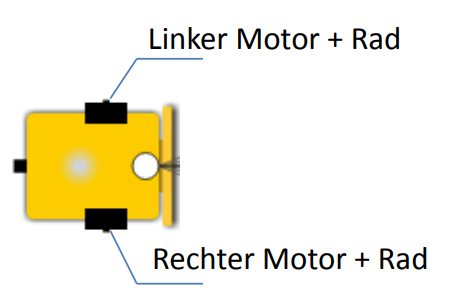
Überlege dir, wie der Roboter trotzdem eine Kurve fahren kann.
3 Kreise fahren - Ein erster Test
Wie du jetzt weißt, müssen die Räder mit unterschiedlicher Geschwindigkeit angetrieben werden. Dazu kannst du in der Kategorie "Aktion" den folgenden Baustein verwenden:
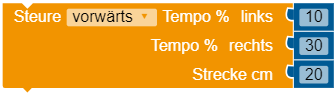
Bei Open Roberta werden die Geschwindigkeiten immer in Prozent der maximalen Geschwindigkeit angegeben. Maximale Geschwindigkeit bedeutet also .
Teste folgende Werte für eine Strecke von
Tempo % links: , Tempo % rechts:
Tempo % links: , Tempo % rechts:
Tempo % links: , Tempo % rechts:
4 Was ist Geschwindigkeit?
Um das richtige Geschwindigkeitsverhältnis berechnen zu können, benötigst du die richtige Formel für die Geschwindigkeit.
Überlege dir nun mit Hilfe der Aufgabe was Geschwindigkeit eigentlich bedeutet. In der Aufgabe wird für die Geschwindigkeit die Variable , für die Strecke und für die Zeit .
Laden
5 Geschwindigkeit - Das richtige Verhältnis bestimmen
Nun soll das richtige Verhältnis für die Geschwindigkeiten berechnet werden. Die Formel für Geschwindigkeit ist:
oder auch
Die Geschwindigkeit und die Strecke sind für beide Reifen unterschiedlich, aber die Zeit ist bei beiden gleich, weil sich sonst ein Reifen länger drehen würde als der andere.
Du erhältst also zwei Formeln für die Geschwindigkeit der Reifen:
Reifen außen:
Reifen innen:
Das Verhältnis ist also:
| ↓ | Durch einen Bruch wird geteilt, indem man mit dem Kehrbruch multipliziert. | ||
| ↓ | Kürze mit | ||
Für das richtige Verhältnis der Geschwindigkeiten brauchst du also die Strecken der einzelnen Räder.
Überlege dir, welche Strecke die einzelnen Räder jeweils zurücklegen. Mache dann auf der nächsten Kursseite weiter.
6 Strecken - Die Kreisbahn
Eine Zeichnung soll dir helfen zu verstehen, welche Strecken die einzelnen Räder zurücklegen:
Der Roboter soll sich mittig auf dem Kreis bewegen. Nachdem die Räder außen am Roboter liegen, bewegen sie sich jeweils auf einer eigenen Kreisbahn. Der Radius des Kreises auf dem der Roboter sich bewegt, hat einen Radius . Das innere Rad bewegt sich also auf einem Kreis mit Radius , also . Das äußere Rad bewegt sich auf einem Kreis mit einem Radius, der um eine halbe Spurbreite größer ist, also .
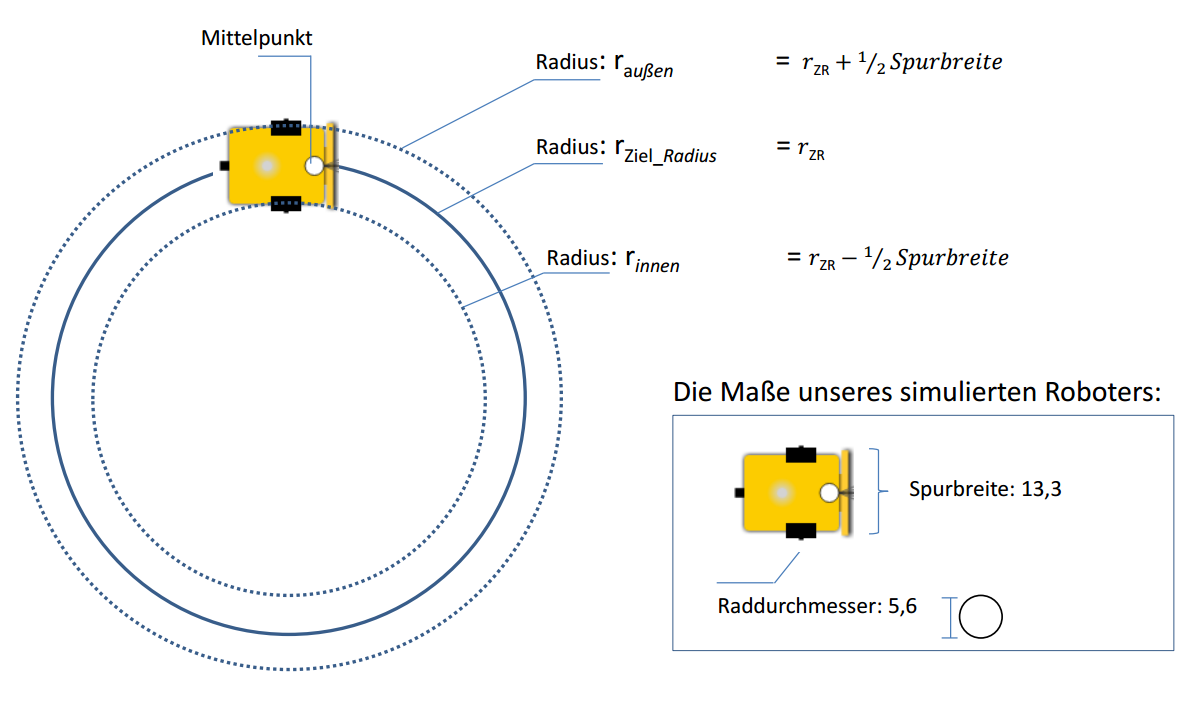
Du hast nun also drei verschiedene Radien, welchen du folgende Bezeichungen geben kannst:
Radius des Kreises auf dem der Roboter fahren soll:
Radius des Kreises auf dem sich der innere Reifen bewegt:
Radius des Kreises auf dem sich der äußere Reifen bewegt:
Versuche nun selbst die Länge der Strecken des äußeren und inneren Reifens zu berechnen und damit das Verhältnis der Geschwindigkeiten zu bestimmen. Probiere es in Open Roberta aus! Die Lösung findest du auf der nächsten Seite.
7 Strecken und Geschwindigkeiten berechnen
Die Strecken und sind jeweils eine Kreisbahn. Um diese zu berechnen, musst du den Umfang des jeweiligen Kreises berechnen. Hierfür benötigst du die dazugehörige Formel:
Die Strecke ist also
und die Strecke
Die beiden Strecken kannst du nun in die Formel für das Geschwindigkeitsverhältnis einsetzen.
kann gekürzt werden
Wichtig: Du musst die Geschwindigkeit für einen Motor vorgeben, um die zweite Geschwindigkeit im richtigen Verhältnis zu bestimmen. Deshalb löst du die Formel wie folgt nach auf:
8 Formel anwenden - selbst Rechnen
Wie kannst du die errechnete Formel nun anwenden?
Du kannst für eine Geschwindigkeit wählen, zum Beispiel , und damit berechnen.
Geschwindigkeit angegeben. Wähle deshalb keine Geschwindigkeit die größer als ist.
Aufgabe
Der Roboter soll einen Kreis mit einem Radius von und einer Geschwindigkeit von fahren. Du hast also folgende Werte:
Durch einsetzen in die Formel erhälst du folgende Gleichung:
| ↓ | Einsetzen der Werte | ||
| ↓ | Bruch vereinfachen | ||
Damit der Roboter den gewünschten Kreis genau einmal abfährt, musst du noch berechnen wie weit er fahren soll. Hierfür verwendest du wieder die Formel für den Umfang eines Kreises:
Formel:
| ↓ | Werte einsetzen | ||
Die nun berechneten Werte kannst du nun im Programm verwenden:
9 Formel anwenden - Direkt im Programm
Alternativ kann die Berechnung auch direkt vom Programm ausgeführt werden. Nutze hierfür die Mathematik Bausteine von Open Roberta
10 Aufgaben
Laden
Laden





