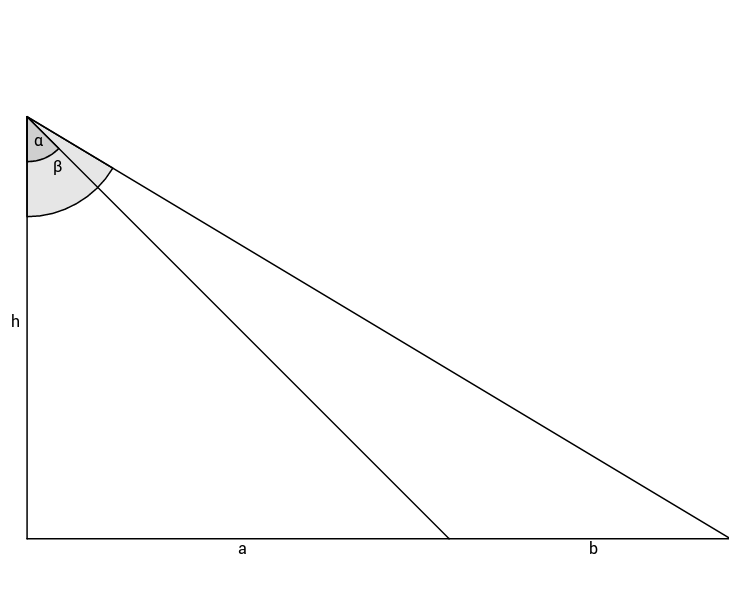
Diese Skizze zeigt ein nicht maßgetreues, rechtwinkliges Dreieck mit der Höhe und den Winkeln und .
Berechne die Seitenlängen und .
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Diese Skizze zeigt ein nicht maßgetreues, rechtwinkliges Dreieck mit der Höhe und den Winkeln und .
Berechne die Seitenlängen und .
