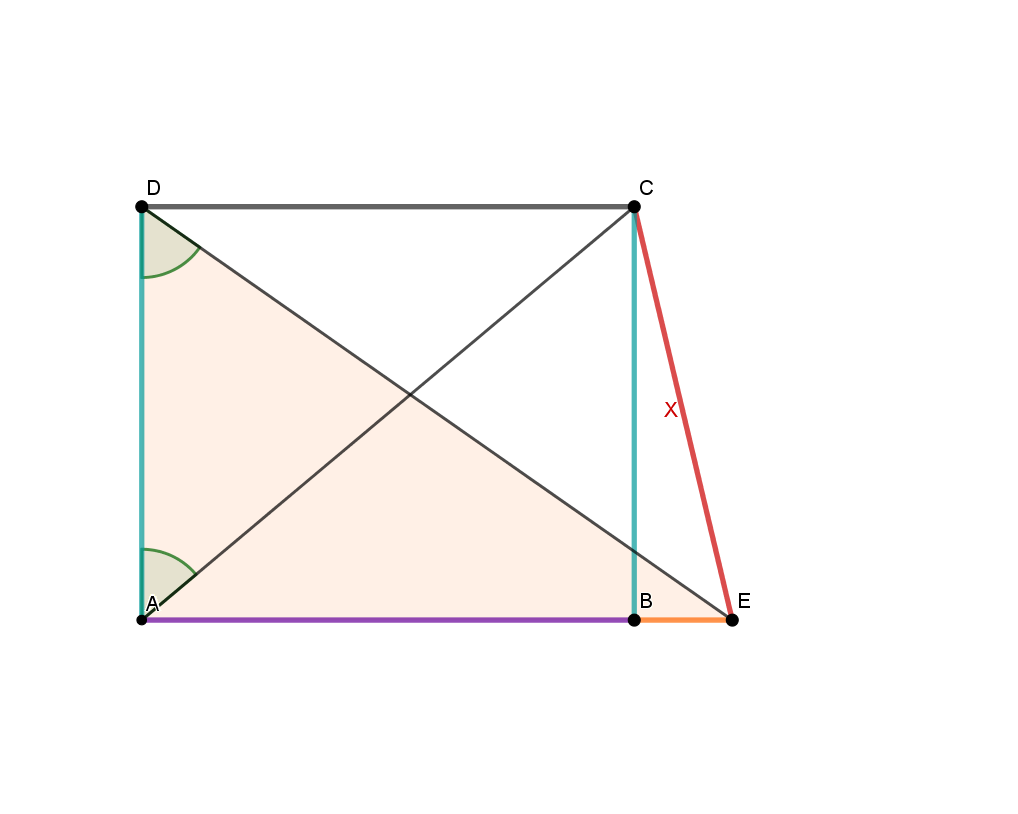
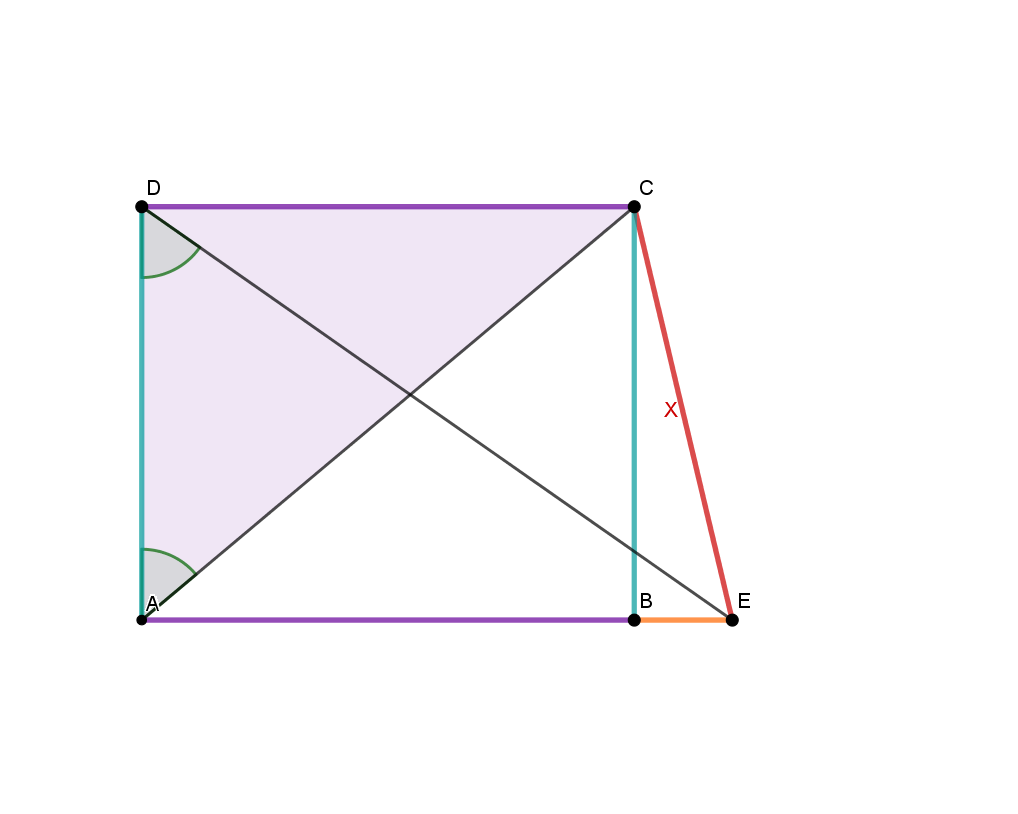
Schwierigere Rechenaufgaben zu den Winkelfunktionen

1
Berechne in einem rechtwinkligen Dreieck mit $a=5\text{ cm}$ und $\alpha= 75°$ die Seitenlänge von $b$ . Runde auf zwei Nachkommastellen.
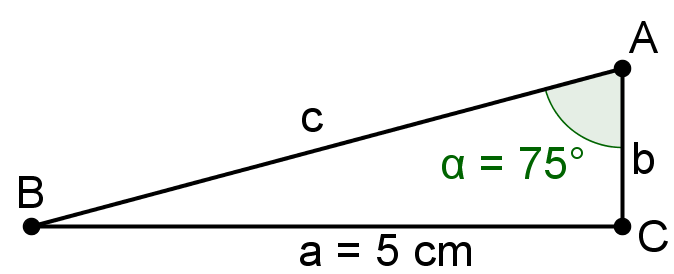cm
2
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
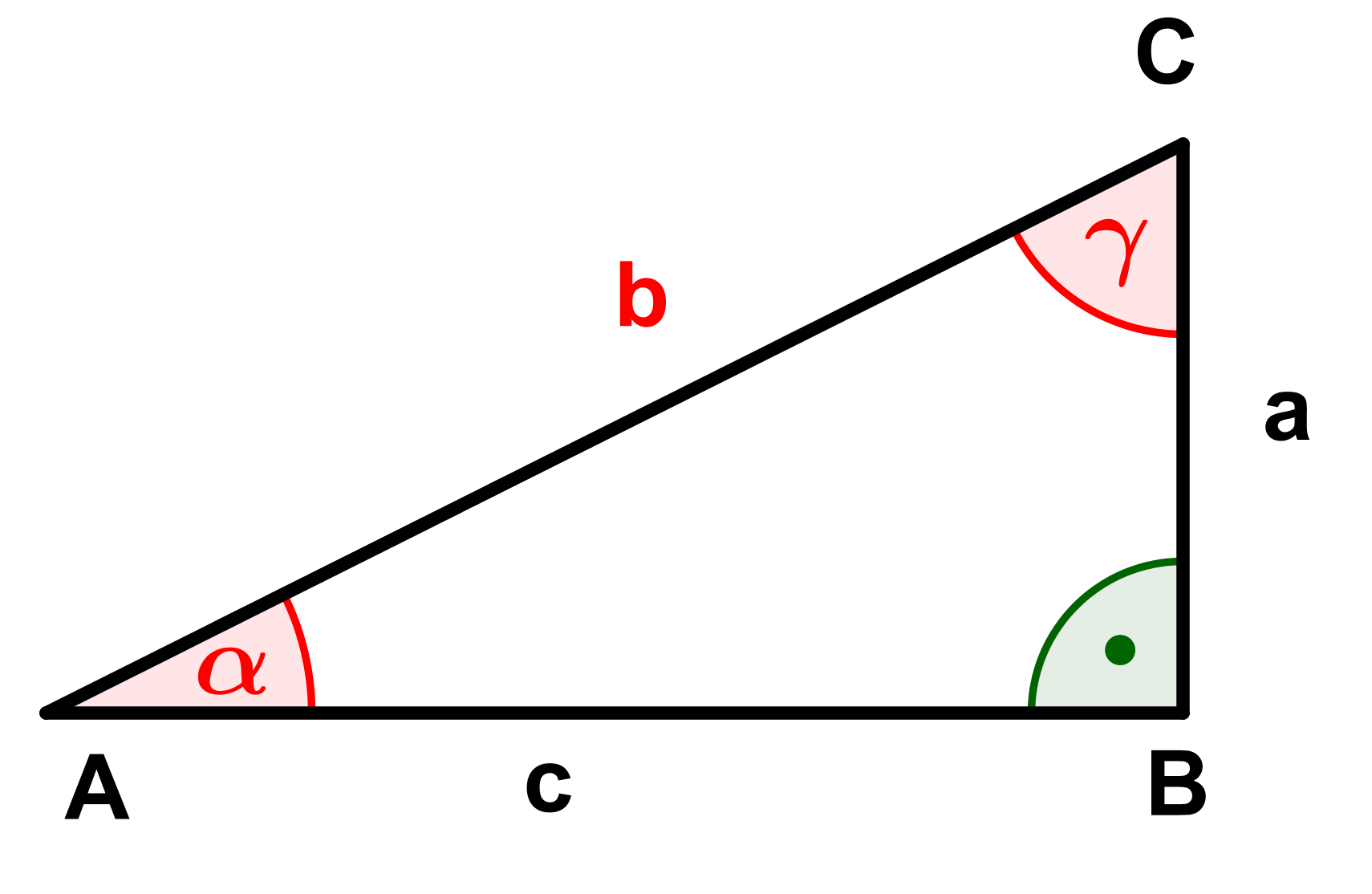
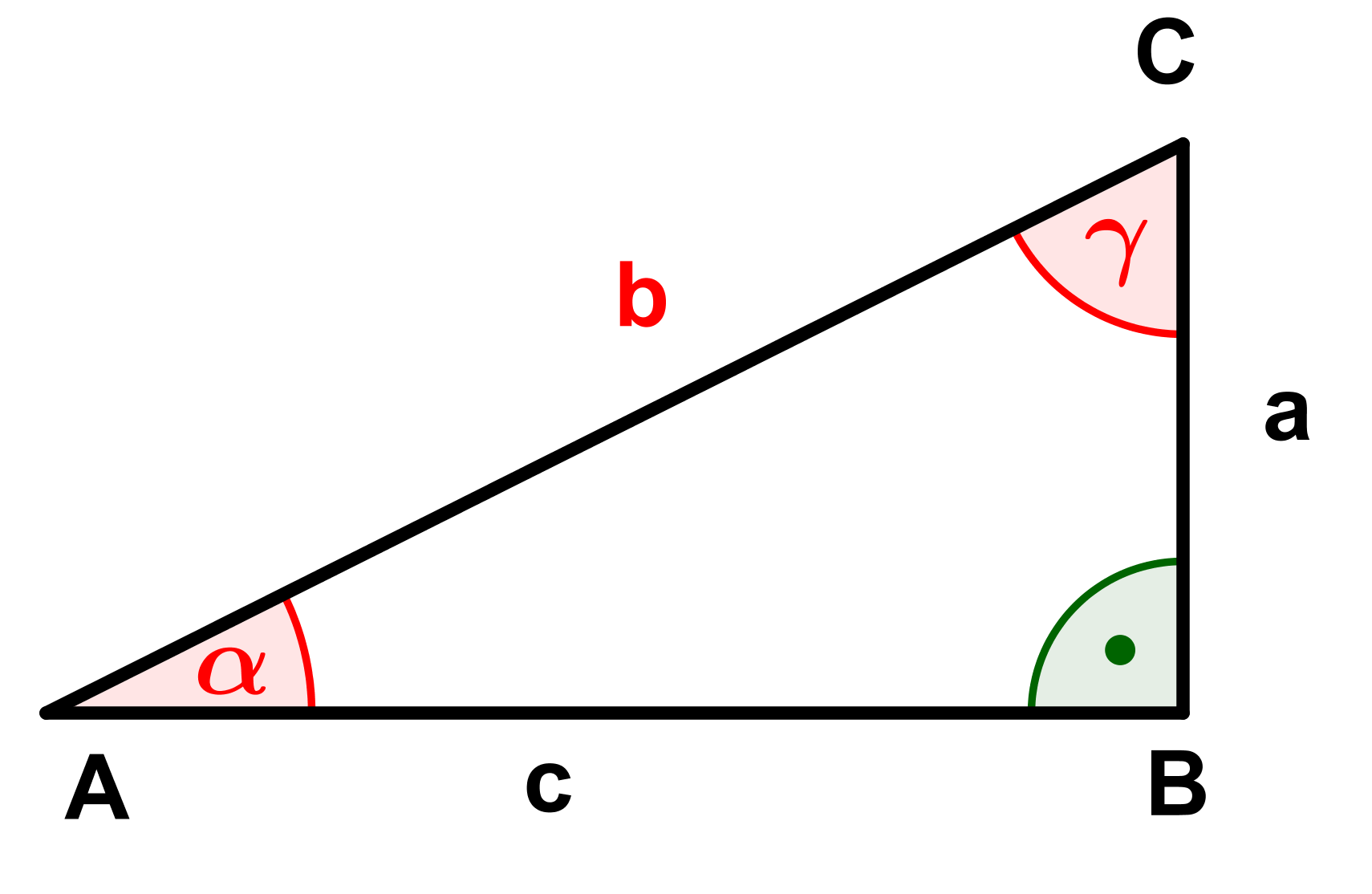
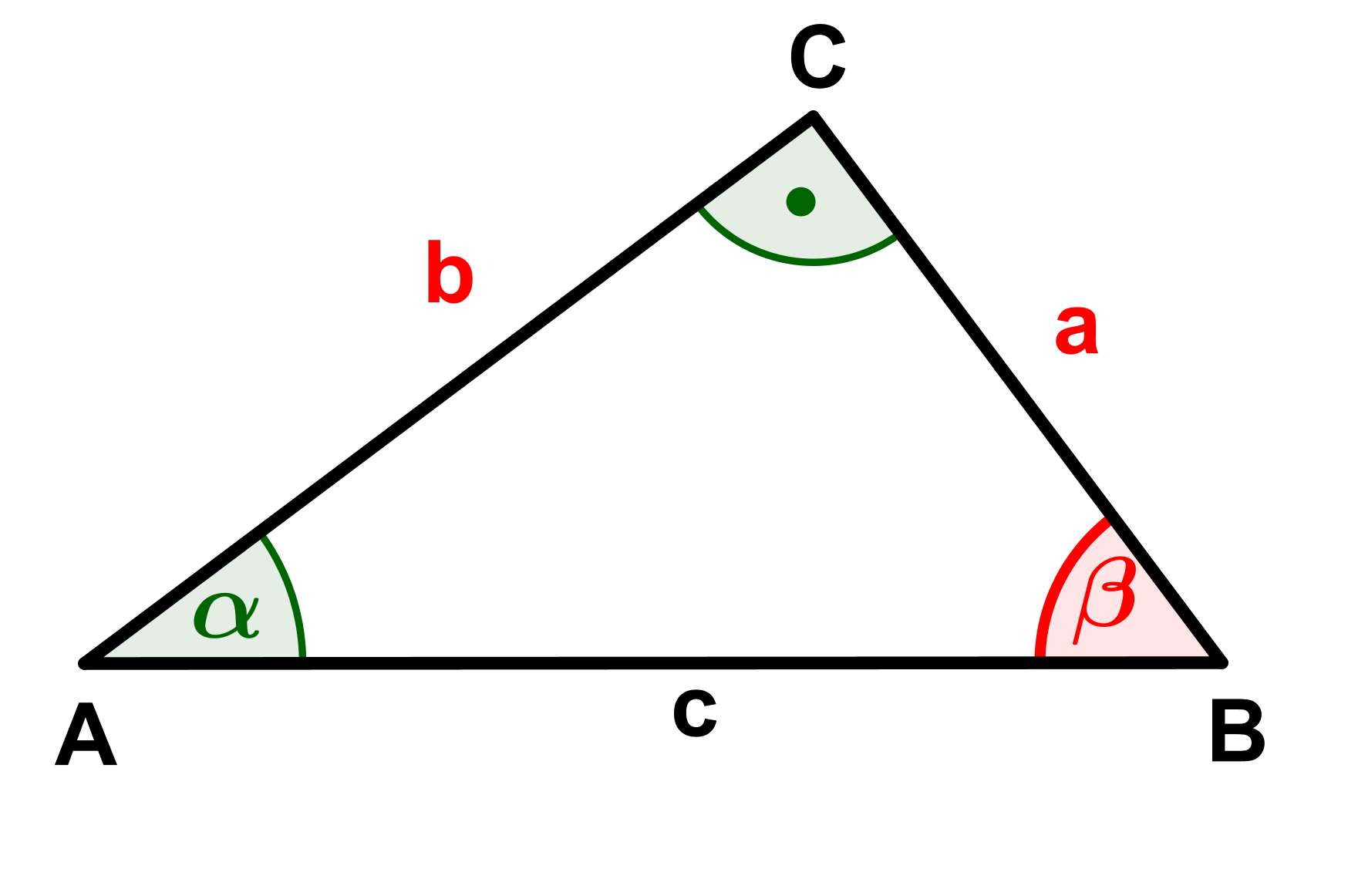
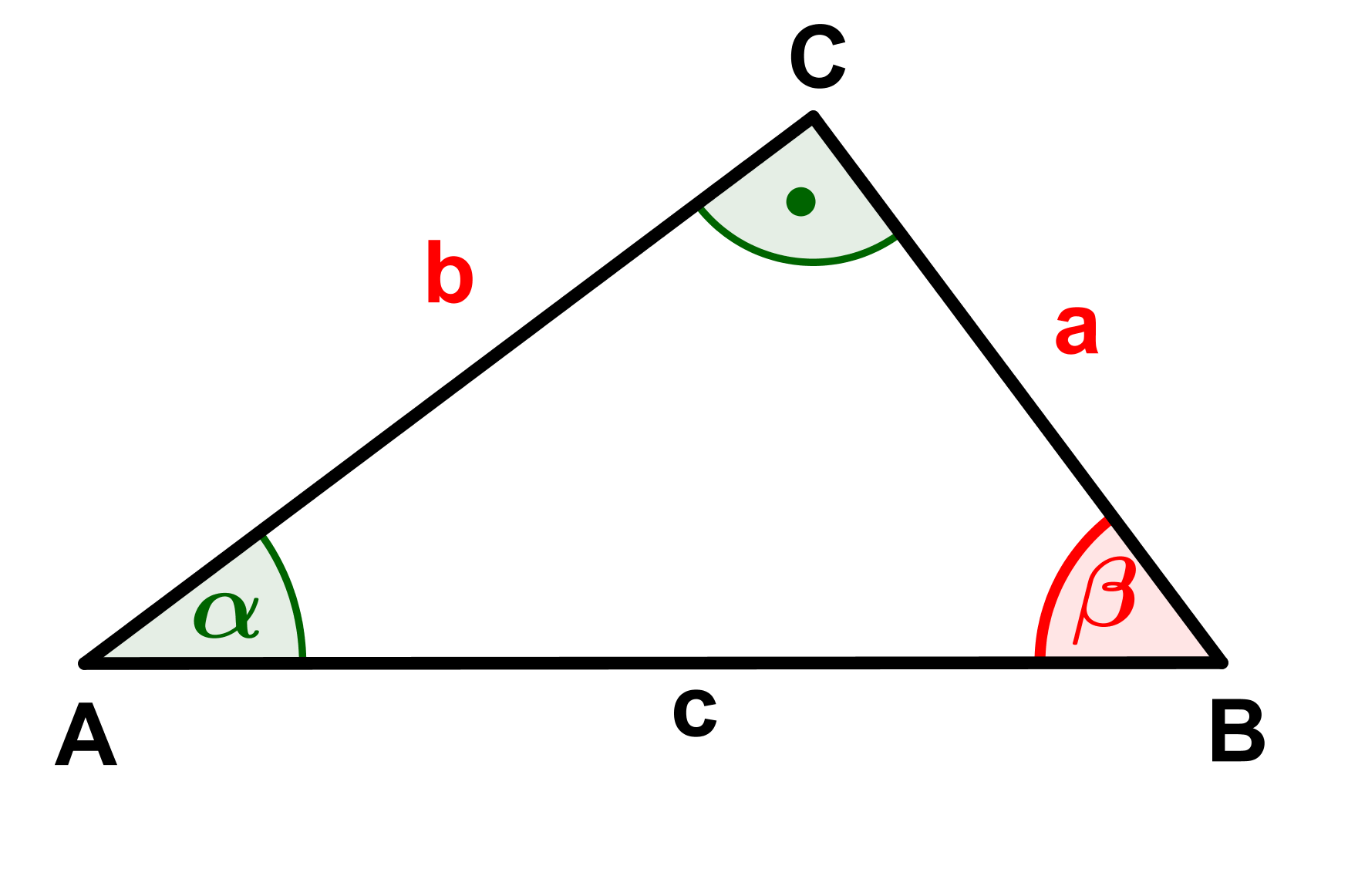
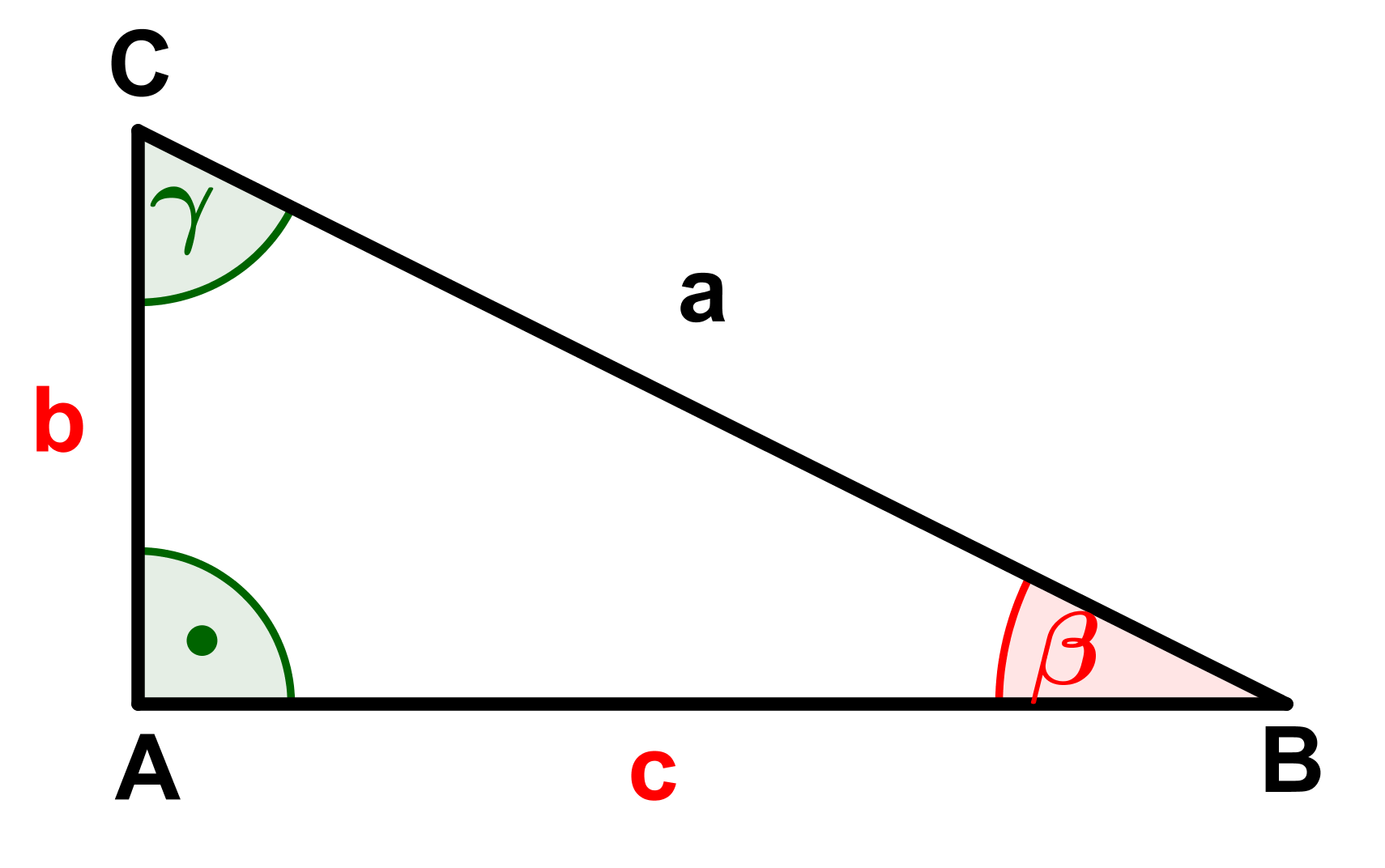
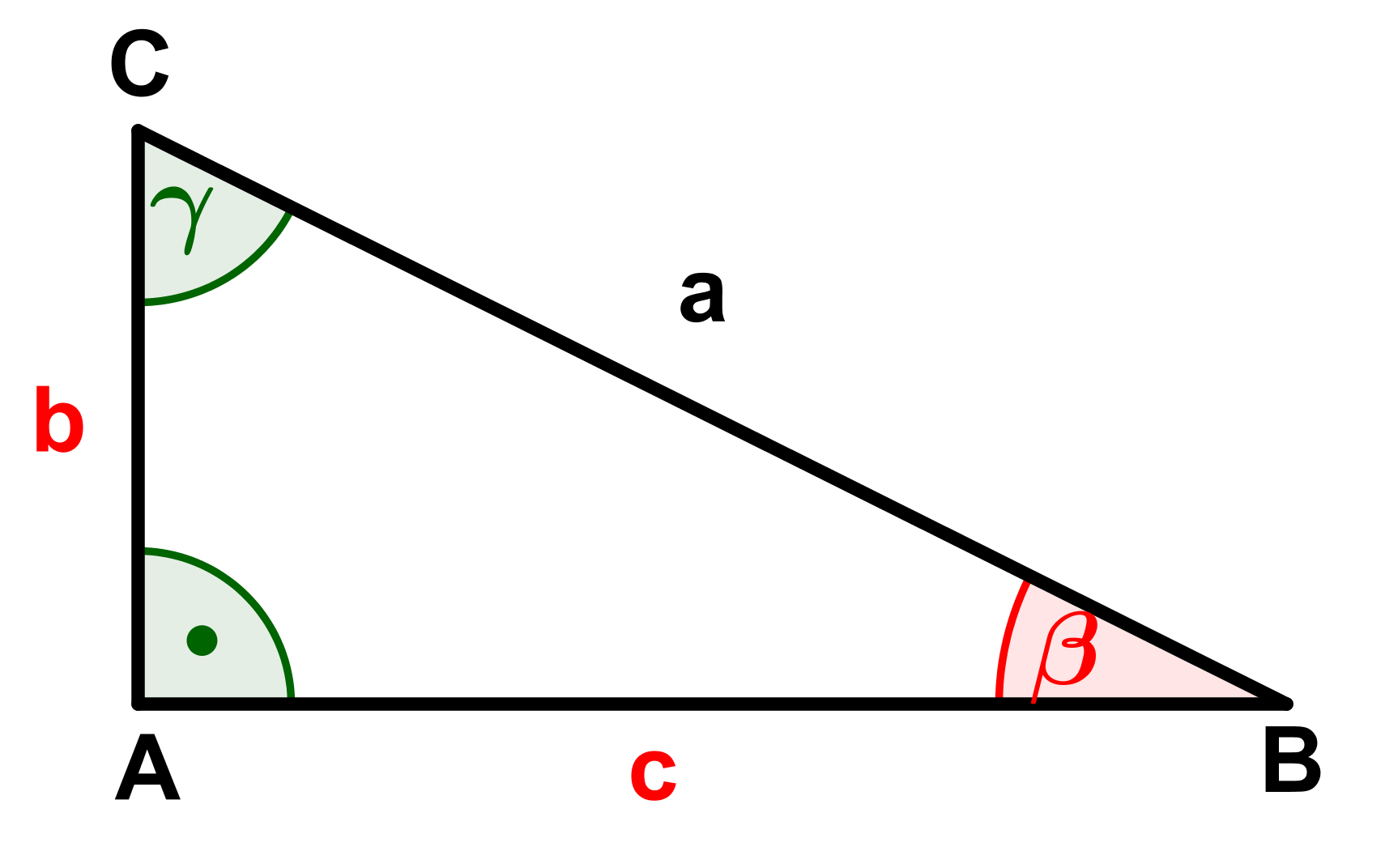
Berechne die fehlenden Seiten und Winkel (rot markiert) der Dreiecke.
1. $\gamma = 90^\circ$
  $a=12{,}7\,\mathrm{cm}$
  $c= 24{,}9\,\mathrm{cm}$
2. $\alpha = 90^\circ$
  $b= 420\,\mathrm m$
  $a= 645\,\mathrm m$
3. $\beta=90^\circ$
  $c=15{,}8\,\mathrm{cm}$
  $a=30{,}7\,\mathrm{cm}$
4. $\gamma=90^\circ$
  $\alpha=35^\circ$
  $c=12{,}5\,\mathrm{cm}$
5. $\alpha=90^\circ$
  $\gamma=40{,}3^\circ$
  $a=10{,}5\,\mathrm{cm}$
3
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
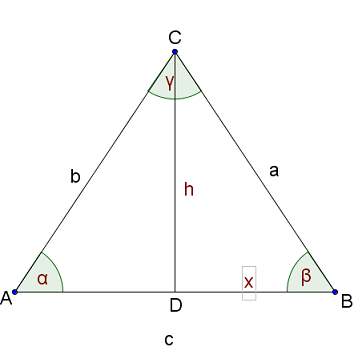
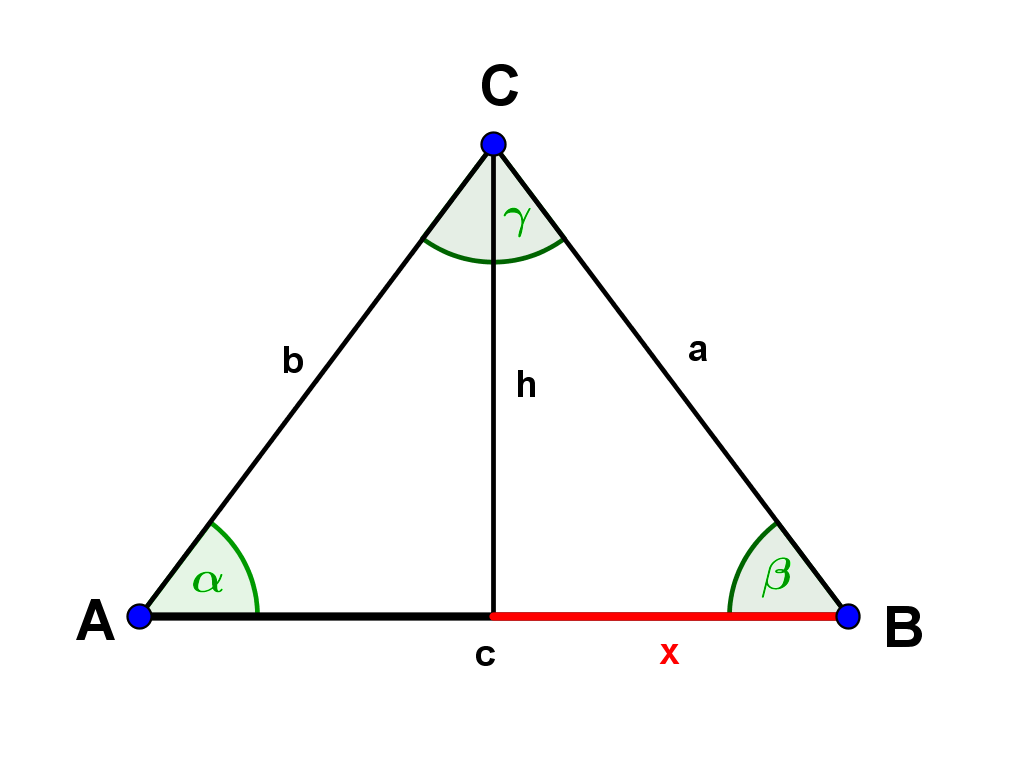
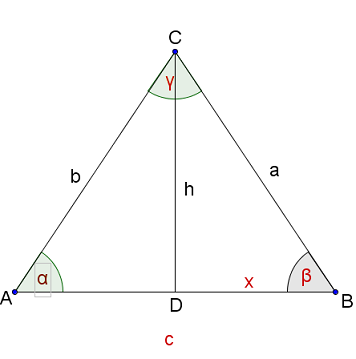
Berechne die fehlenden Seiten und Winkel des gleichschenkligen Dreiecks ABC mit $a=b$ . Beachte, dass wir allgemeine gleichschenklige Dreiecke betrachten, die nicht unbedingt rechtwinklig sind..
1. a=44,2cm
  c=63,4cm
2. a=114,5m
  $\alpha$ =32,3°
3. c=35,4cm
  $\beta$ =43,9°
4. h=14,8cm
  $\alpha=\beta=$ 28,3°
5. a=146,4m
  h=58,4m
4
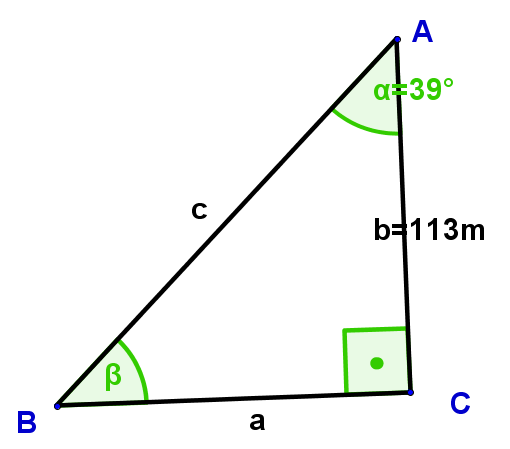
Ein Dreieck mit rechtem Winkel bei C, mit der Seite $b=113m$ hat den Winkel $\alpha=39^\circ$ . Fertige zunächst eine Skizze an und berechne dann alle fehlenden Seiten sowie den Winkel $\beta$ .
5
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
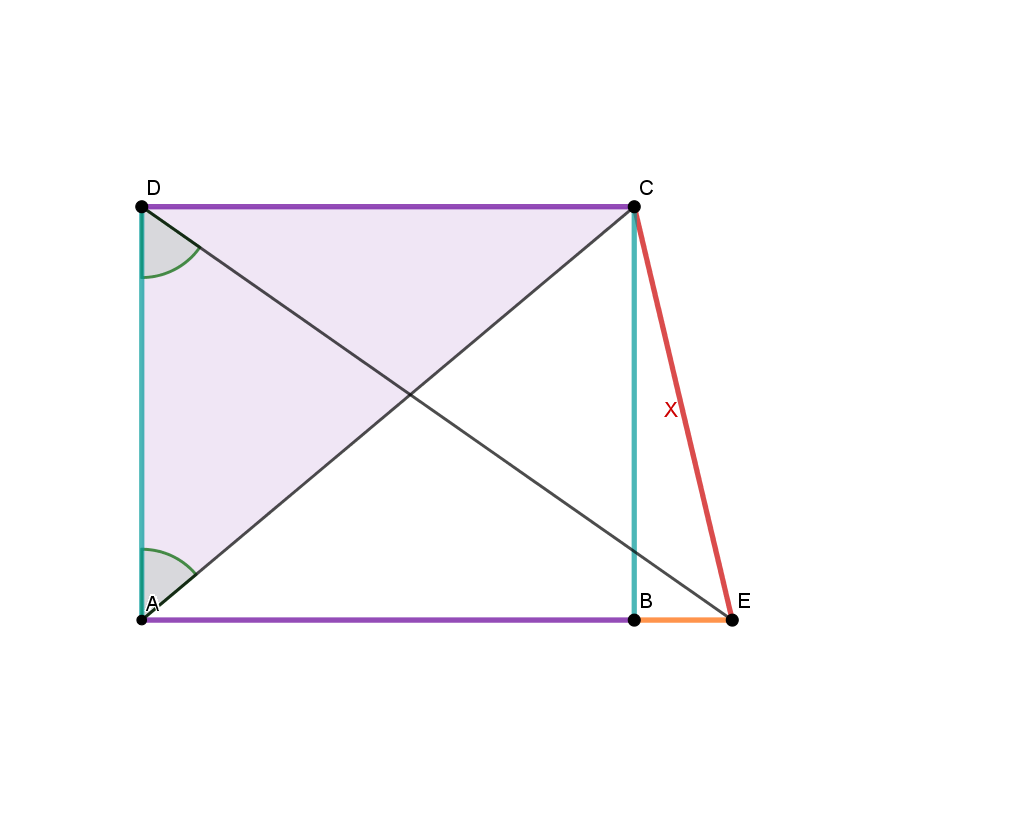
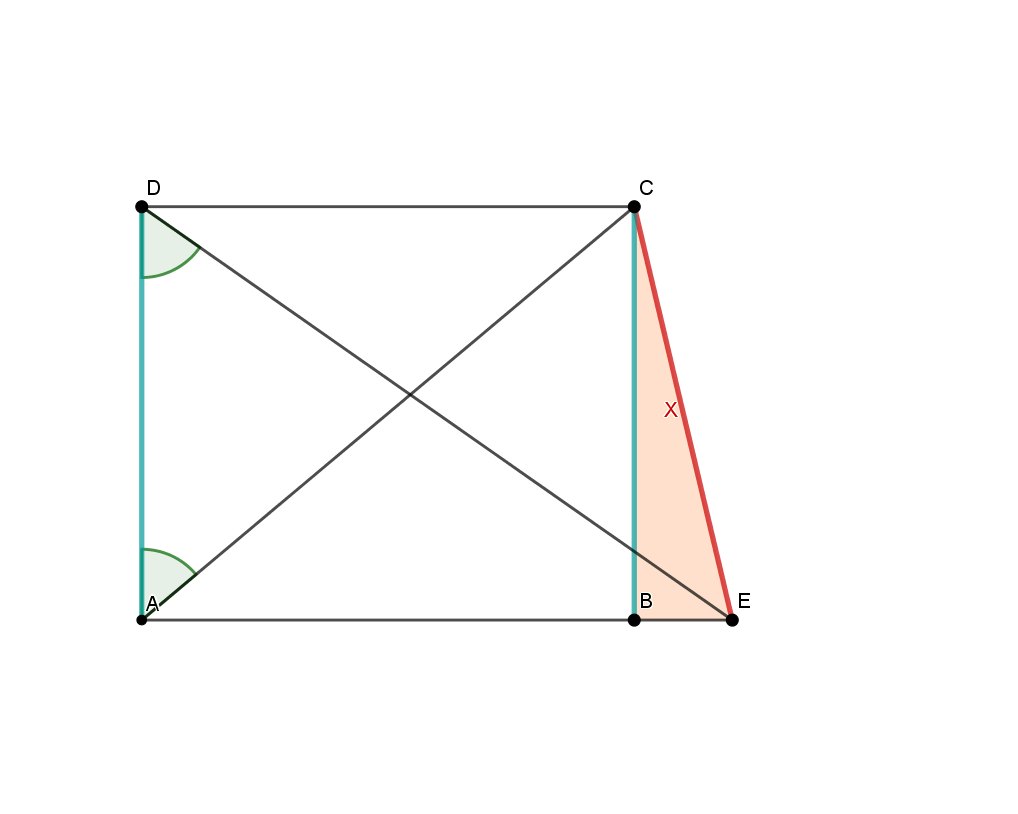
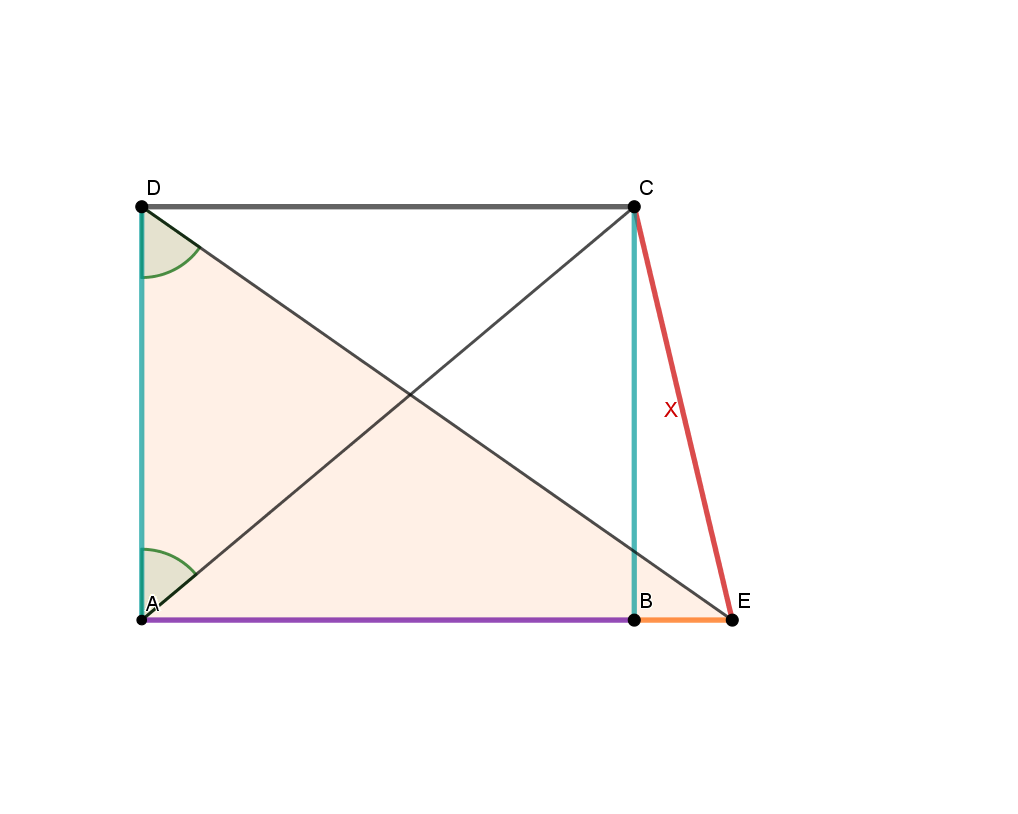
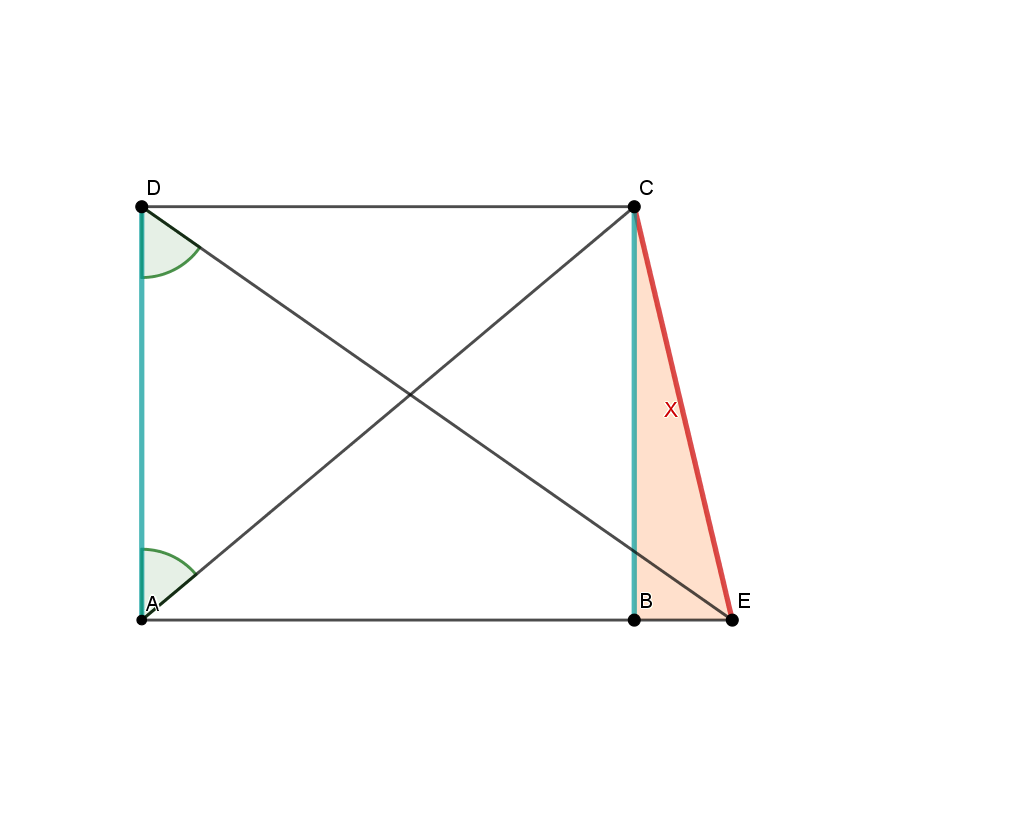
Skizziere ein Rechteck mit den Seiten a=7cm und b=18cm und berechne die Winkel
1. zwischen einer Diagonalen und den Seiten
2. zwischen beiden Diagonalen
6
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
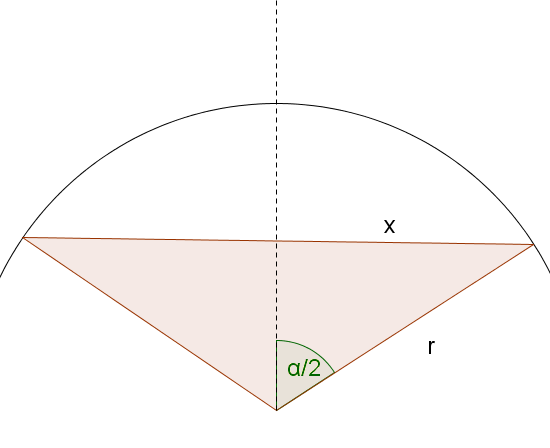
Im Kreis mit dem Radius $r=10~\text{cm}$ gehört zur Sehne $s$ der Mittelpunktswinkel $\alpha=84^\circ$
Wie lang ist die Sehne?
cm
7
123mathe.de (Gilt für: Aufgabenstellung)Dieses Werk steht unter der freien Lizenz CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann
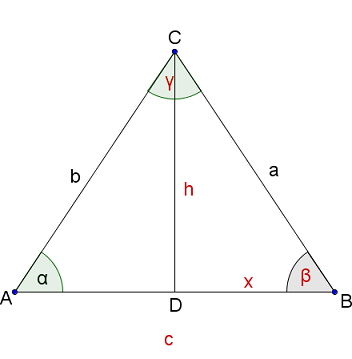
Berechne die fehlenden Seiten und Winkel des gleichschenkligen Dreiecks ABC mit a=b.
1. a = 44,2cm
  c = 63,4cm
2. a = 114,5m
  $\alpha$ = 32,3°
3. c = 35,4cm
  $\beta$ = 43,9°
4. $h_c$ = 14,8cm
  $\alpha$ = 28,3°
5. a = 146,4m
  $h_c$ = 58,4m
8
Diese nicht maßstabsgetreue Skizze zeigt ein Trapez mit den Längen:
$\overline{\mathrm{AD}}=7\mathrm m,\;\measuredangle\mathrm{DAB}=\measuredangle\mathrm{DCB}=\measuredangle\mathrm{CDA}=90^\circ,\;\measuredangle\mathrm{CAD}=50^\circ,\;\measuredangle\mathrm{ADE}=55^\circ$
Berechne die rot markierte Strecke $x$
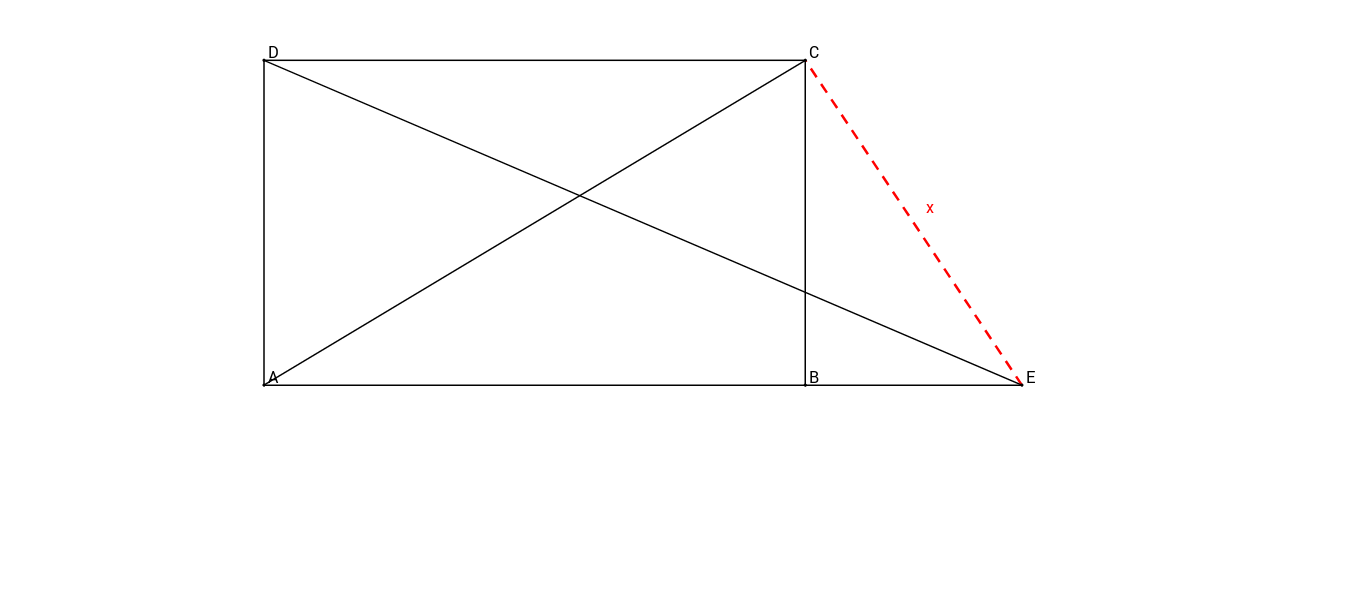m
9
Diese nicht maßstabsgetreue Skizze zeigt ein Drachenviereck $ABCD$ mit Symmetrieachse $AC$ und den Maßen: $\mathrm a=7\;\mathrm{cm}$ , $\mathrm c=6\;\mathrm{cm}$ , $\overline{\mathrm{DB}}=10\;\mathrm{cm}$
Berechne die Winkel $\alpha,\beta$ und $\gamma$ .
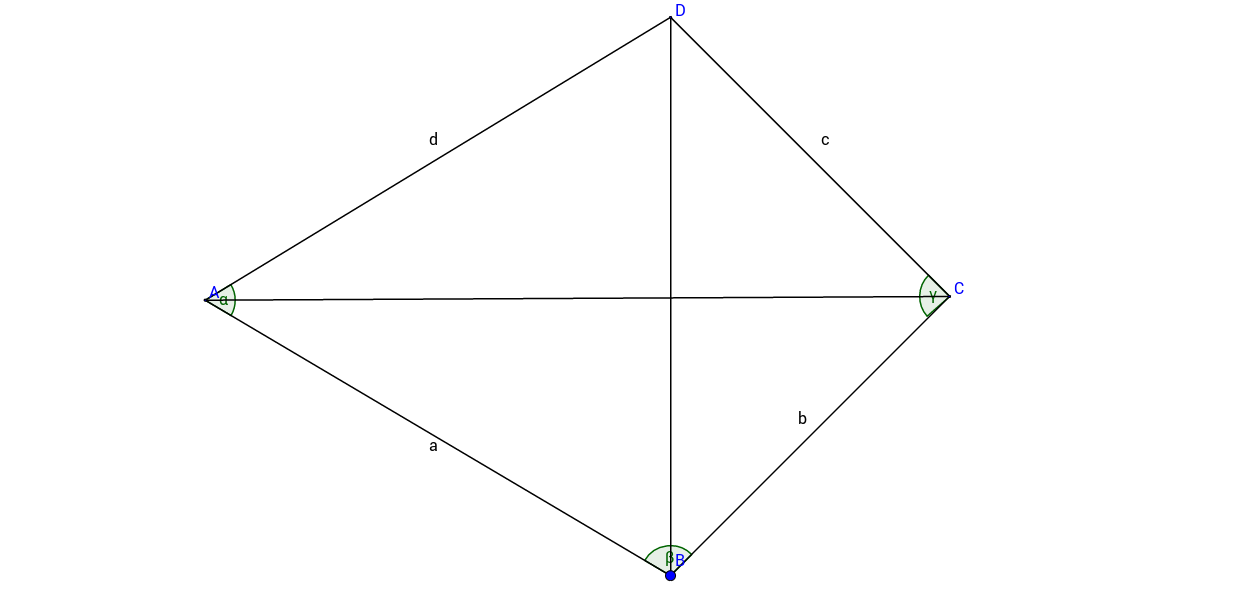
10
Diese Skizze zeigt ein nicht maßgetreues, rechtwinkliges Dreieck mit der Höhe $h=8\,\mathrm{cm}$ und den Winkeln $\mathrm\alpha=65^\circ$ und $\beta=80^\circ$ .
Berechne die Seitenlängen $a$ und $b$ .

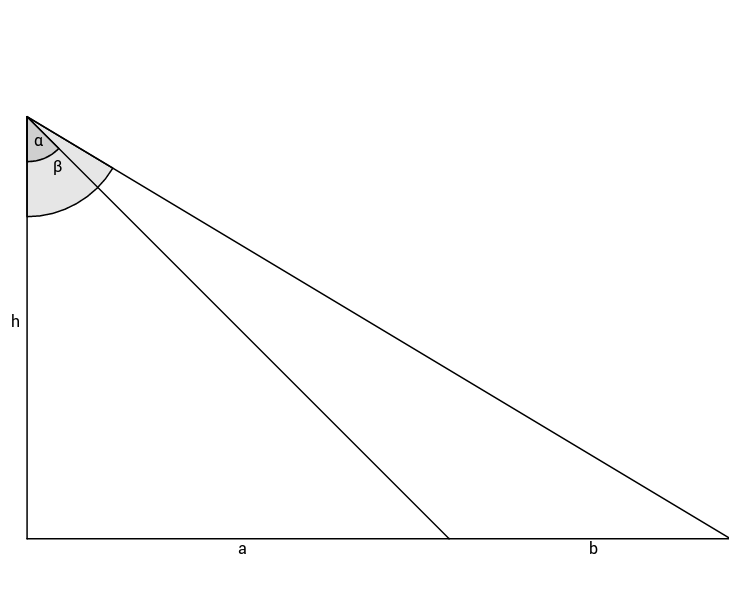
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?