Diese nicht maßstabsgetreue Skizze zeigt ein Trapez mit den Längen:
Berechne die rot markierte Strecke
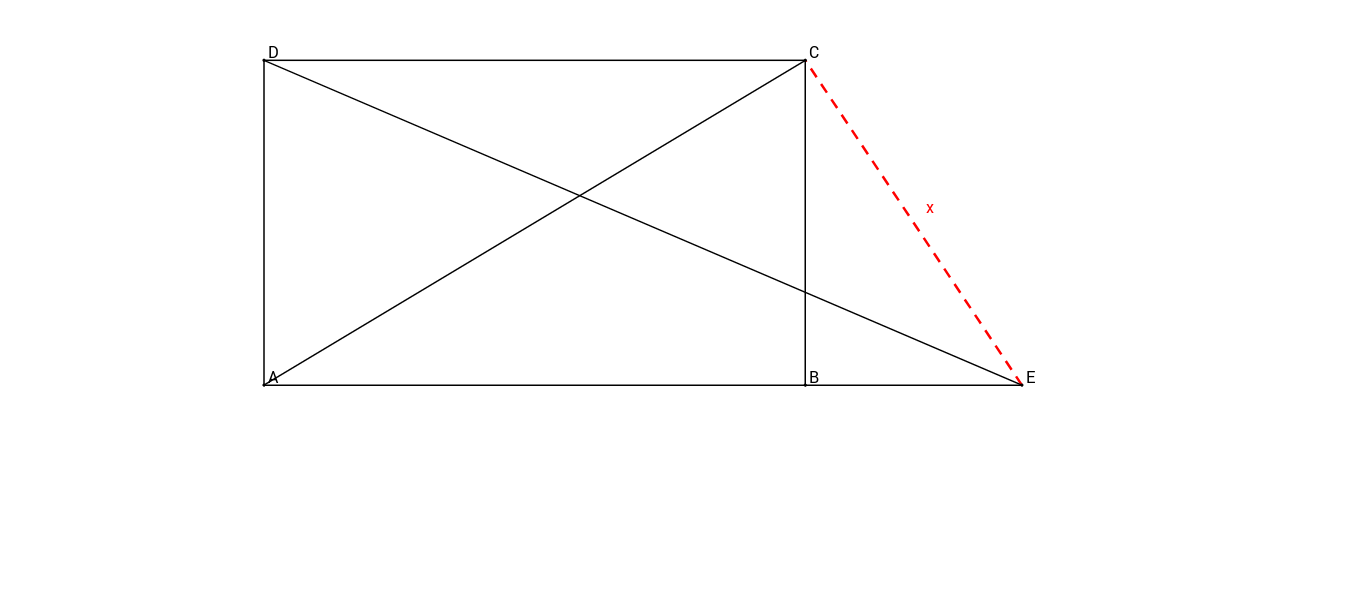
Für diese Aufgabe benötigst Du folgendes Grundwissen: Sinus, Kosinus und Tangens
Tipp: Vorgehen rückwärts in Bildern:
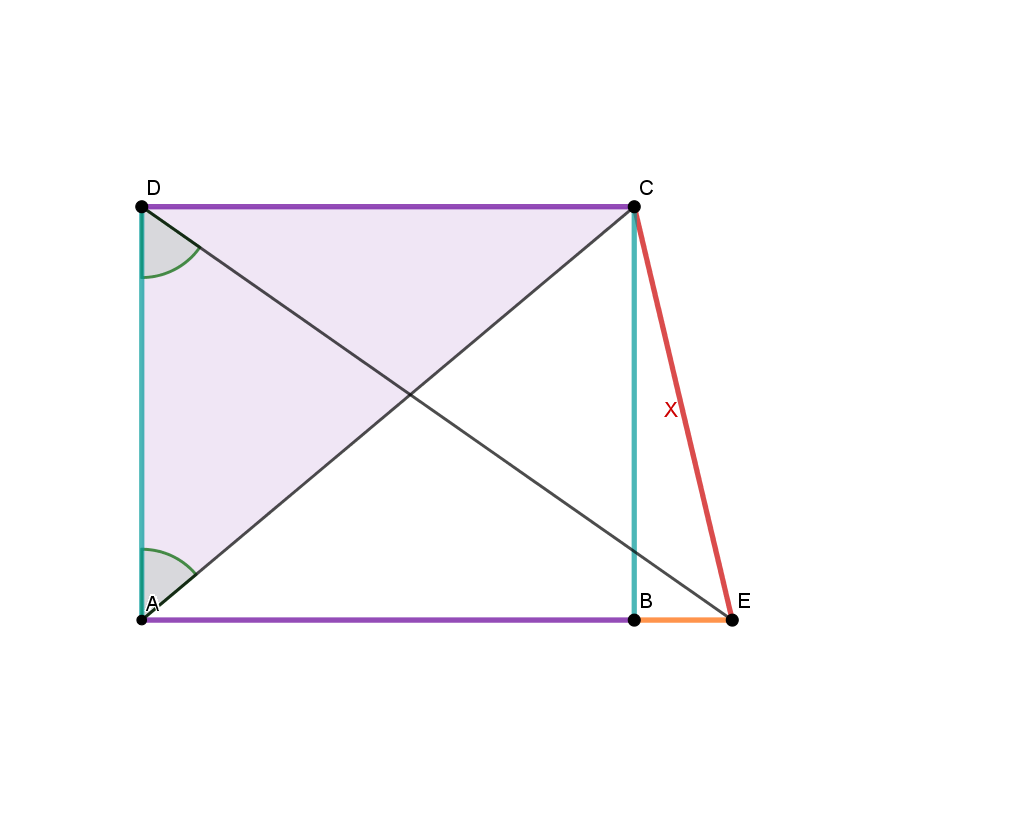
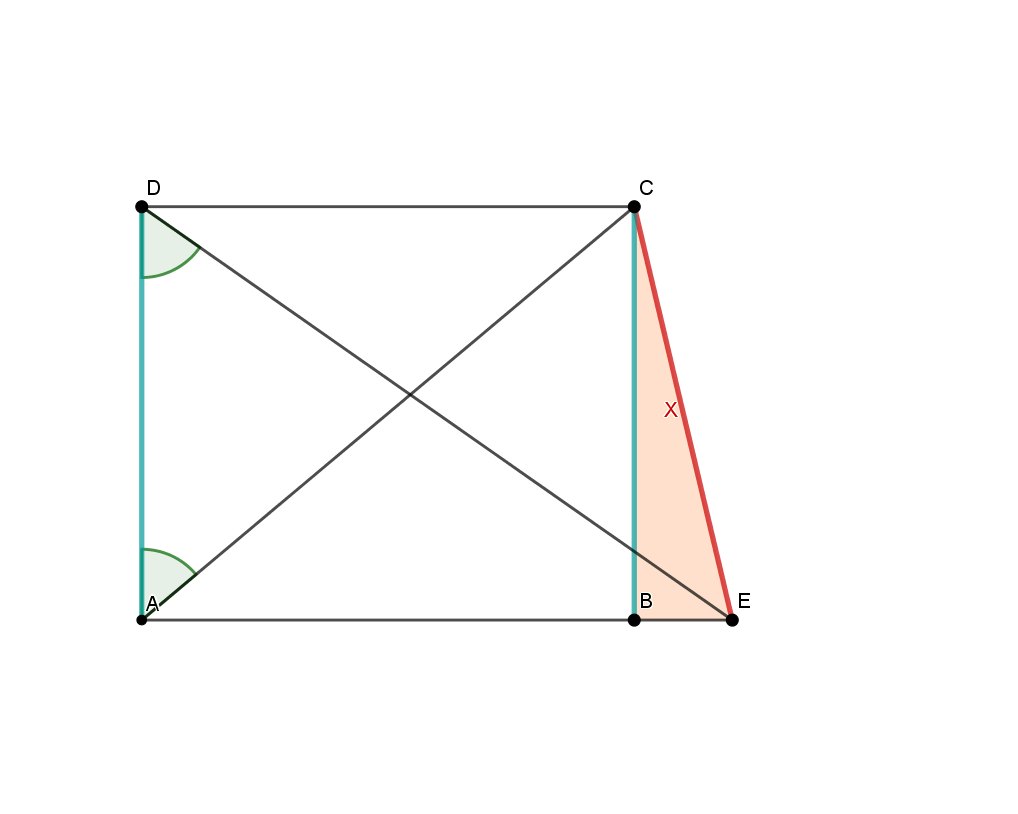
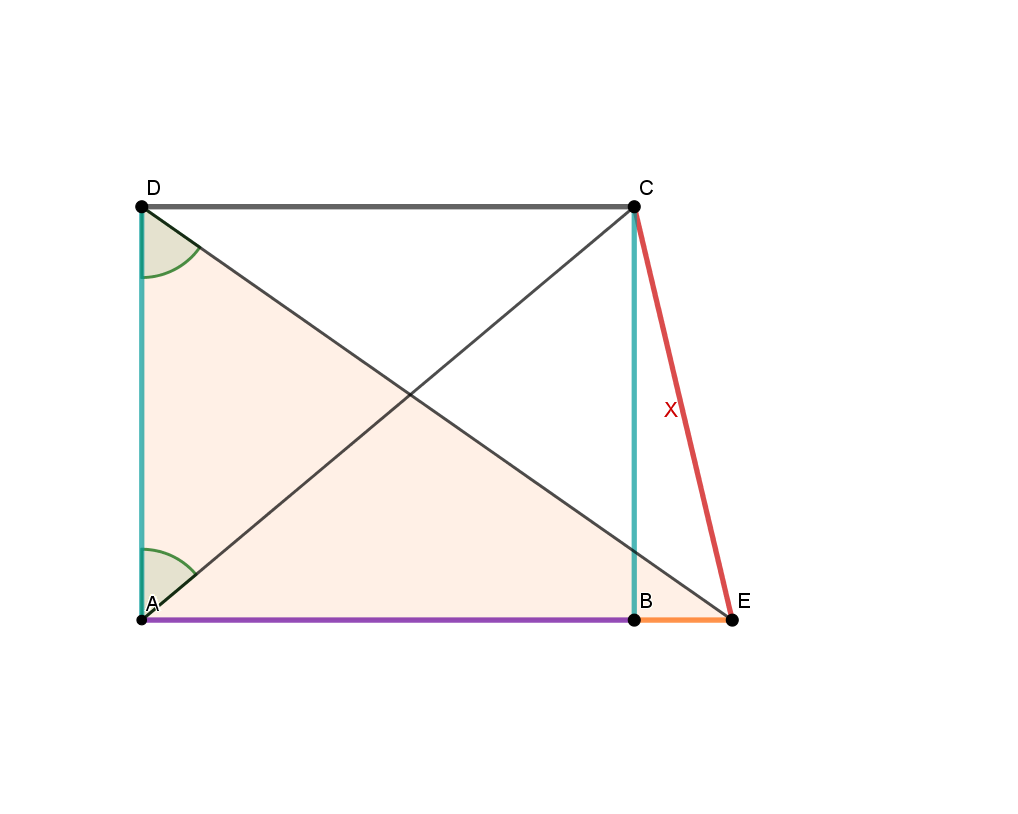
Für diese Aufgabe musst du den Sinus und Kosinus im rechtwinkligen Dreieck sowie den Satz des Pythagoras verwenden können.
Strategie
Wenn du dir zuerst eine Strategie für die Lösung überlegen willst, gehst du am besten rückwärts vor:
Für die Berechnung der Strecke brauchst du z. B. alle anderen Streckenlängen in diesem Dreieck. Die Länge der Strecke kennst du. Sie ist genauso lang wie die Strecke , da sie gegenüberliegende Seiten in einem Rechteck sind. Das heißt, du musst noch bestimmen.
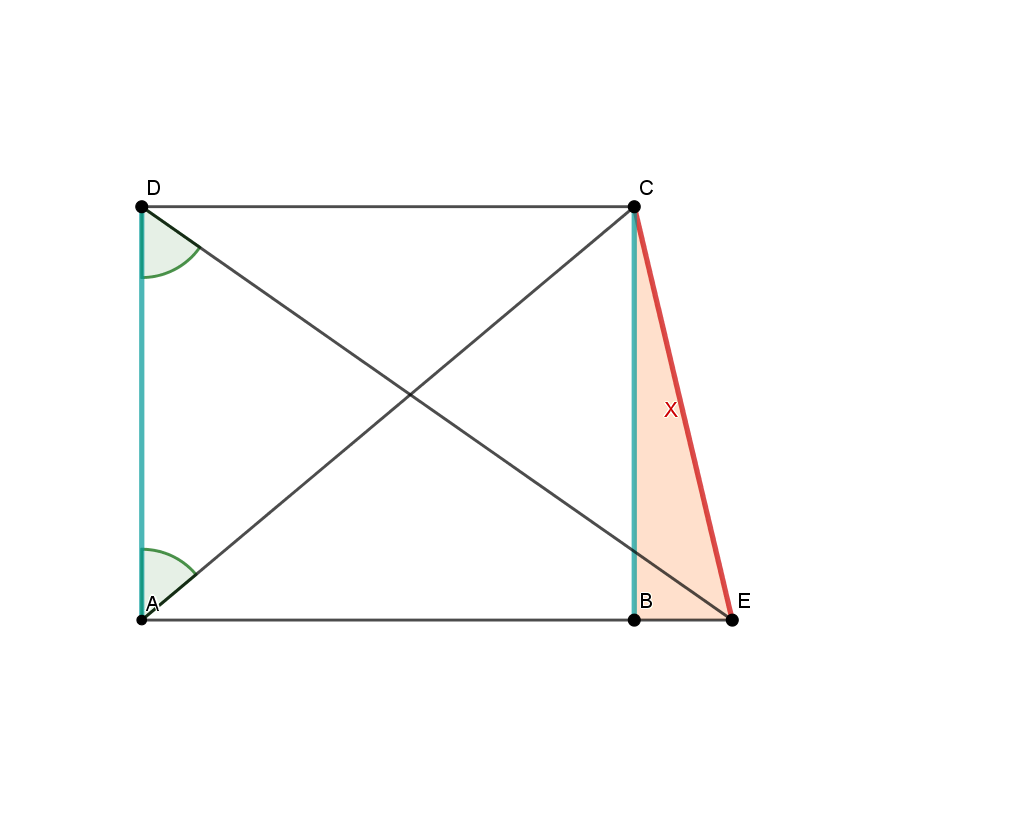
kannst du berechnen, indem du die Strecke von der langen Seite abziehst. kannst du mit Hilfe des Tangens im Dreieck berechnen. Für die Berechnung von kannst du zum Beispiel den Tangens im Dreieck verwenden, da du weißt, dass und als gegenüberliegende Seiten im Rechteck gleich lang sind.
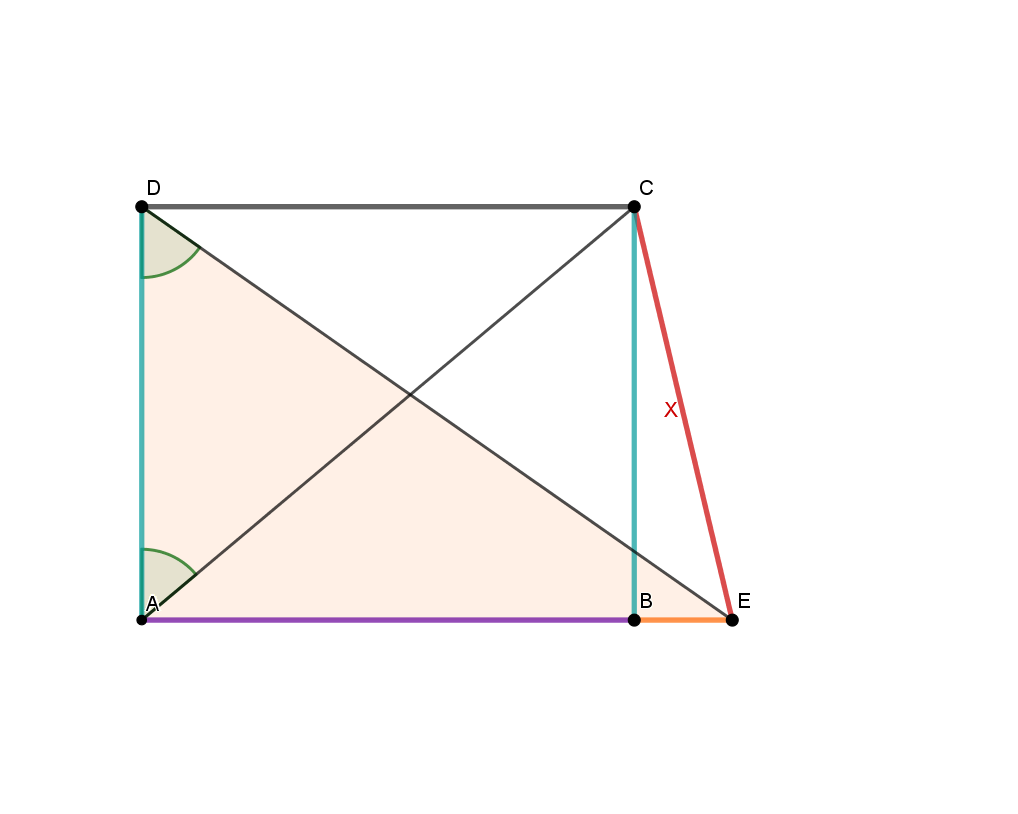
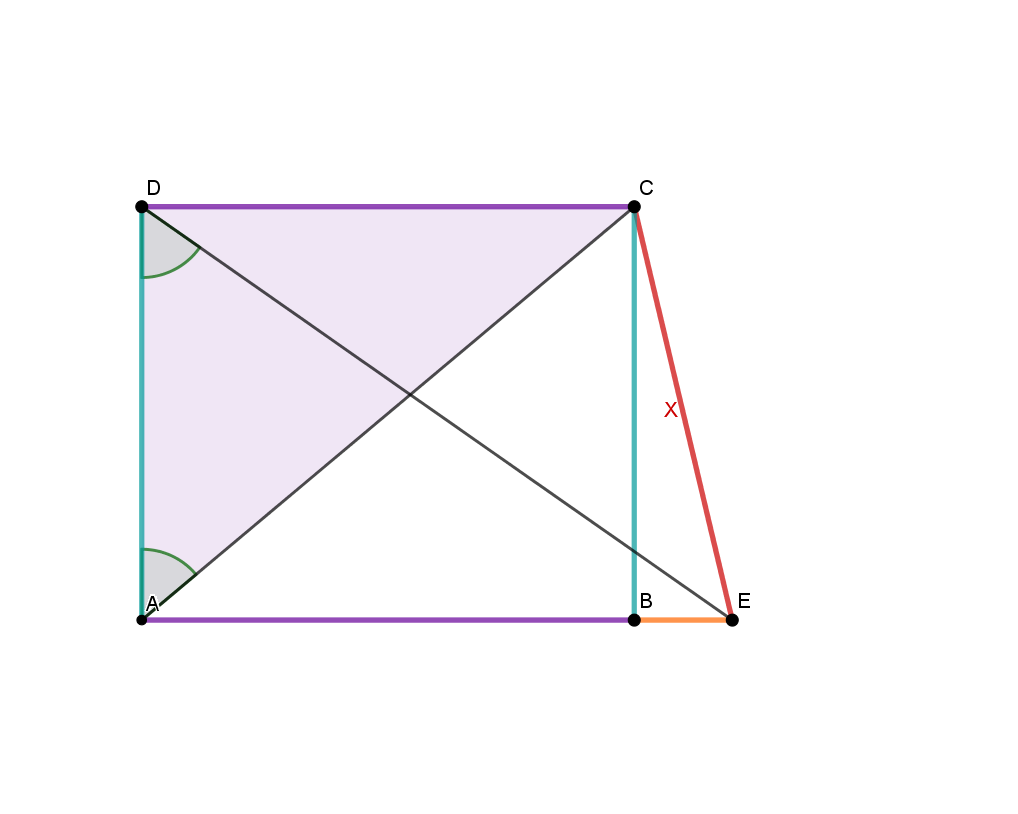
Lösung
Nun kennst du das Vorgehen "von hinten" und kannst es in genau umgekehrter Reihenfolge verwenden, um auf die Länge der Strecke zu kommen:
Berechnung von
Verwende den Tangens im Dreieck mit dem dir bekannten Winkel für die Berechnung von :
Stelle nach der gesuchten Seite um, indem du mit multiplizierst.
Setze die Werte und ein.
Berechnung von
Verwende den Tangens im Dreieck für die Berechnung von , da du und kennst.
Stelle nach der gesuchten Seite um, indem du beide Seiten der Gleichung mit multiplizierst
Setze die Werte ein.
Nun kannst du berechnen:
Berechnung von
Jetzt kannst du die Länge von mit Hilfe des Satzes von Pythagoras ausrechnen. Dabei ist die Hypotenuse.
Stelle nach um, indem du die Wurzel ziehst.
Setze die Werte ein. Denke dabei daran, dass du verwenden kannst, da es sich um gegenüberliegende Seiten im Rechteck handelt.
Die Strecke ist lang.
Hier gibt es, wie sehr oft, nicht nur einen möglichen Lösungsweg. Zum Beispiel kannst du mit einem weiteren Zwischenschritt statt dem Tangens auch den Sinus oder Kosinus verwenden.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
