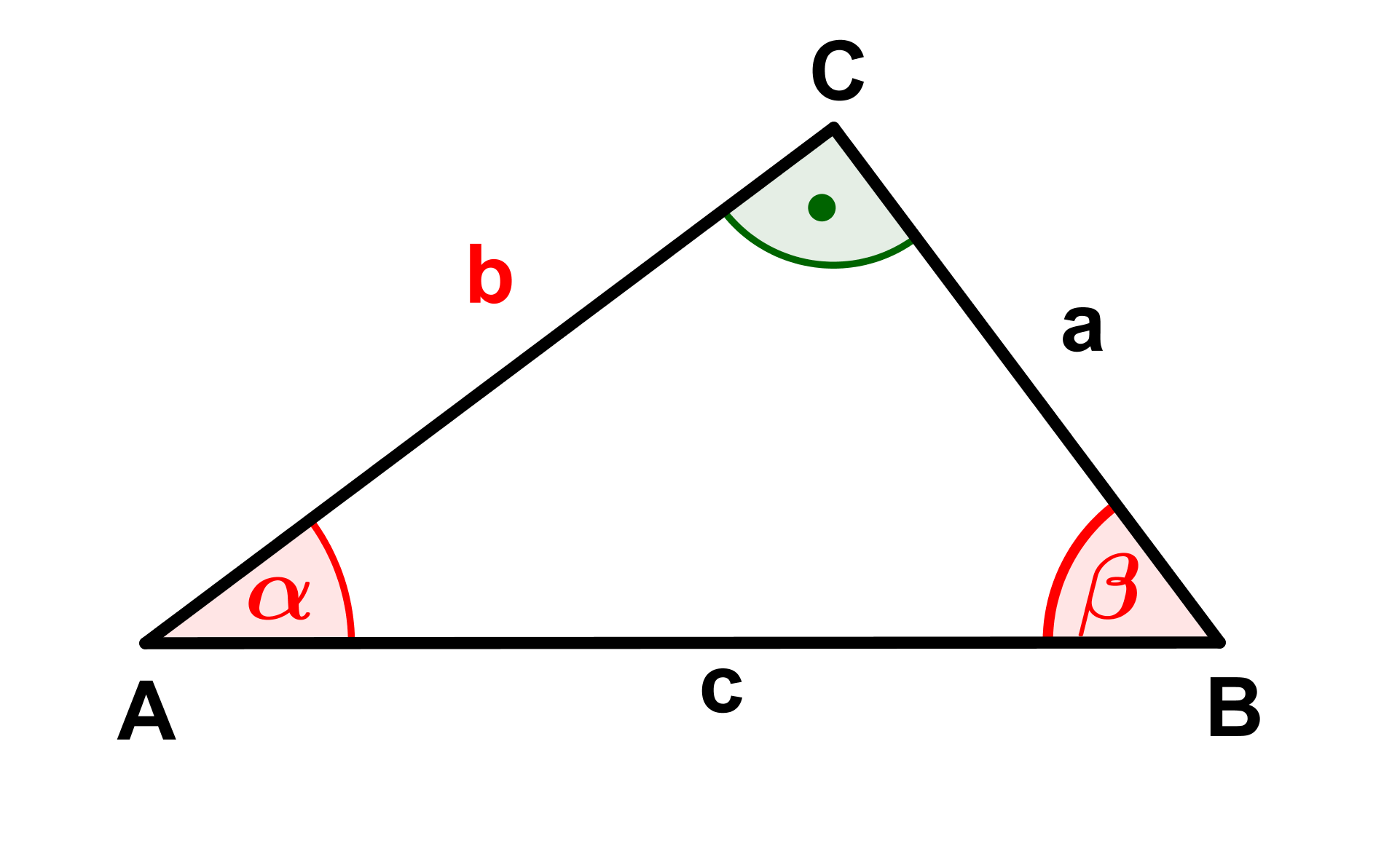
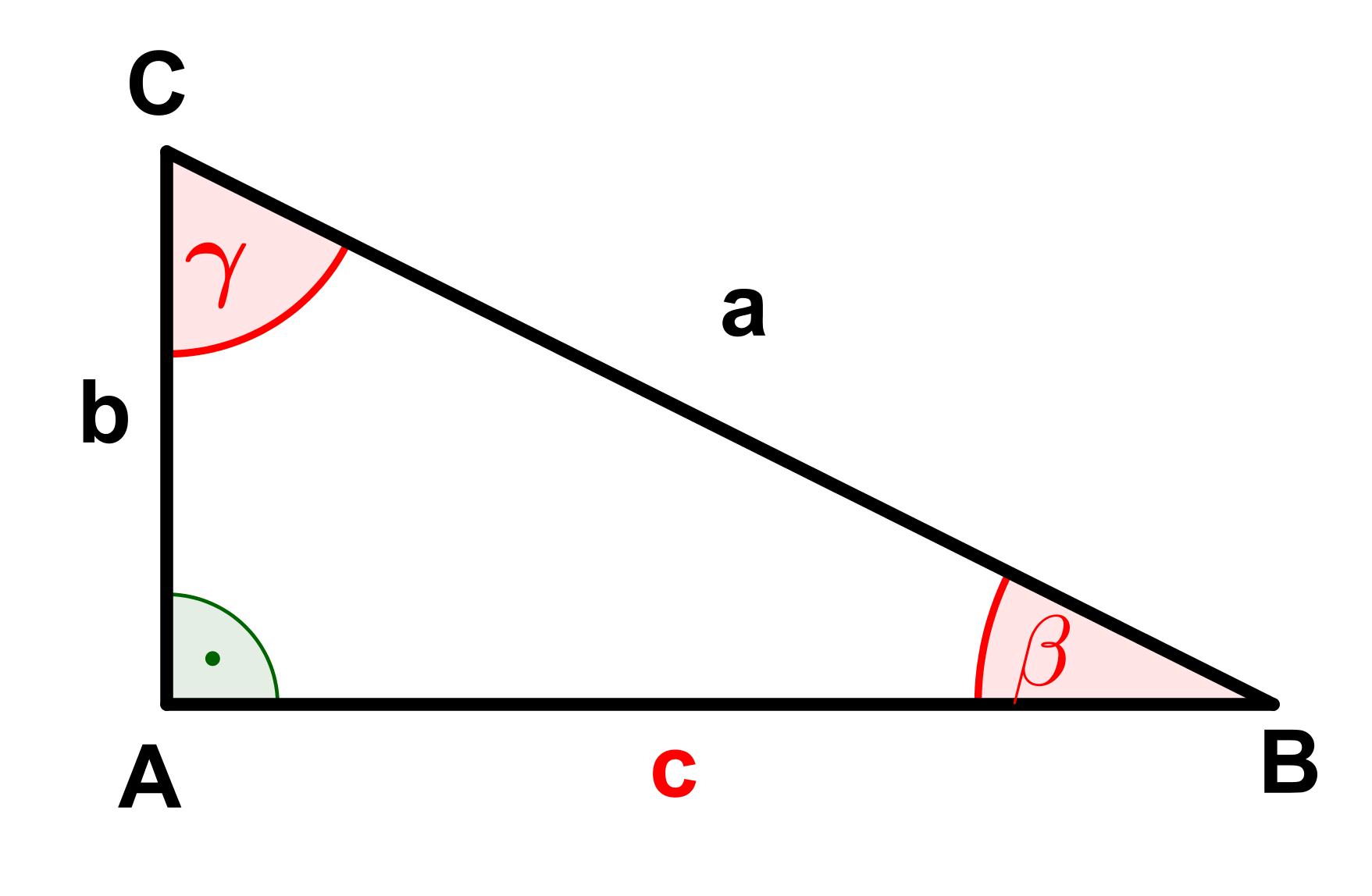
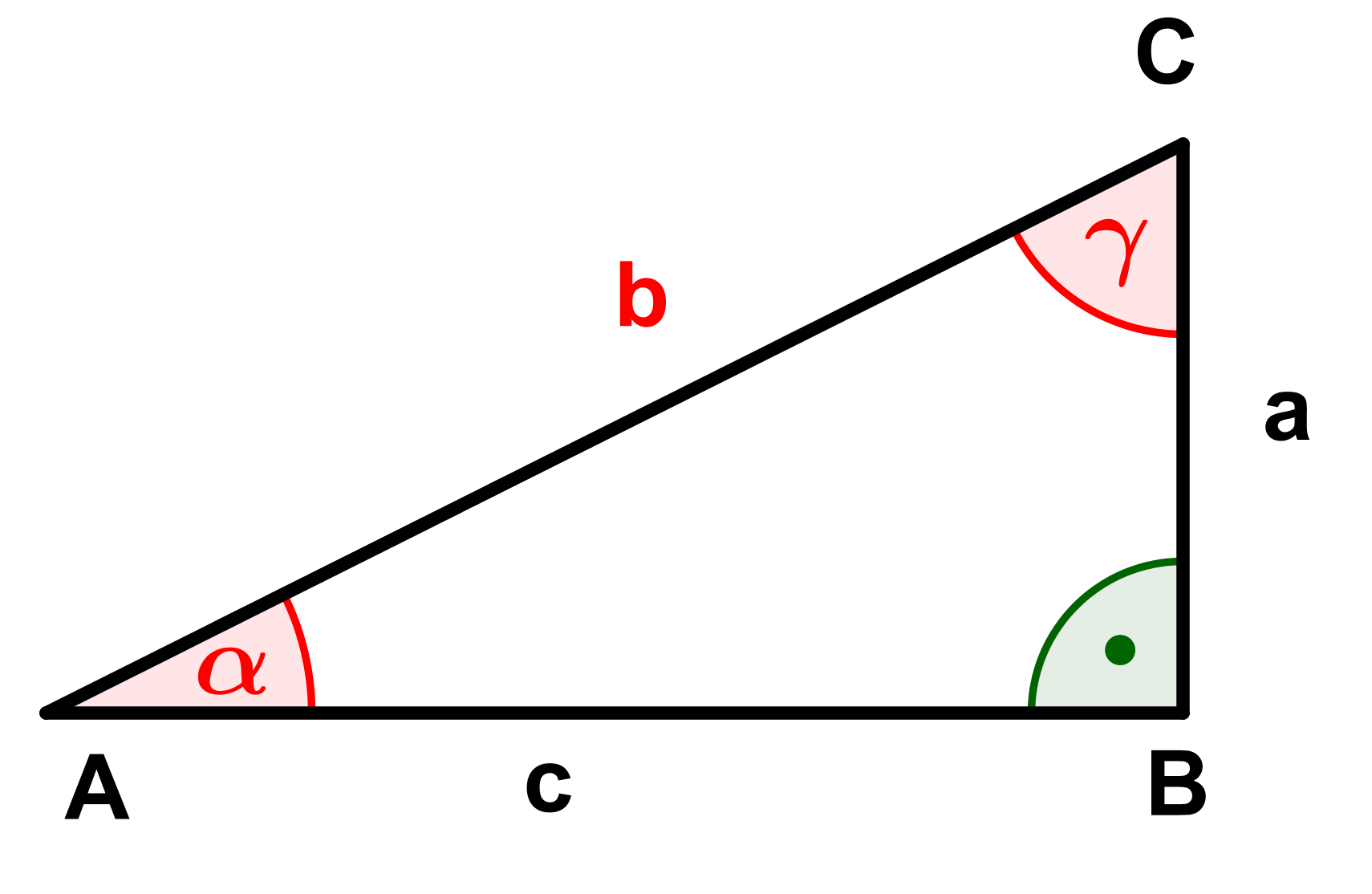
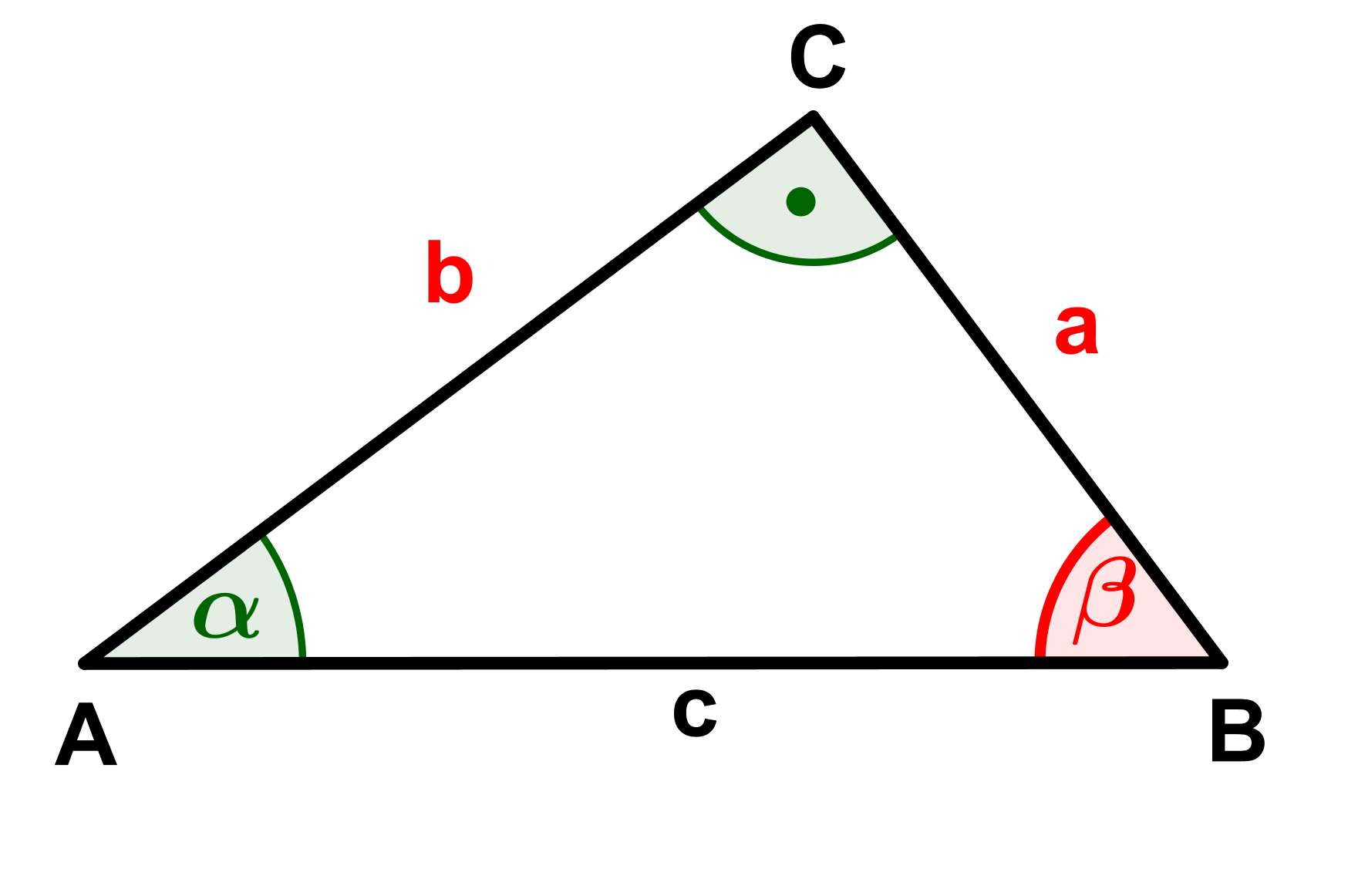
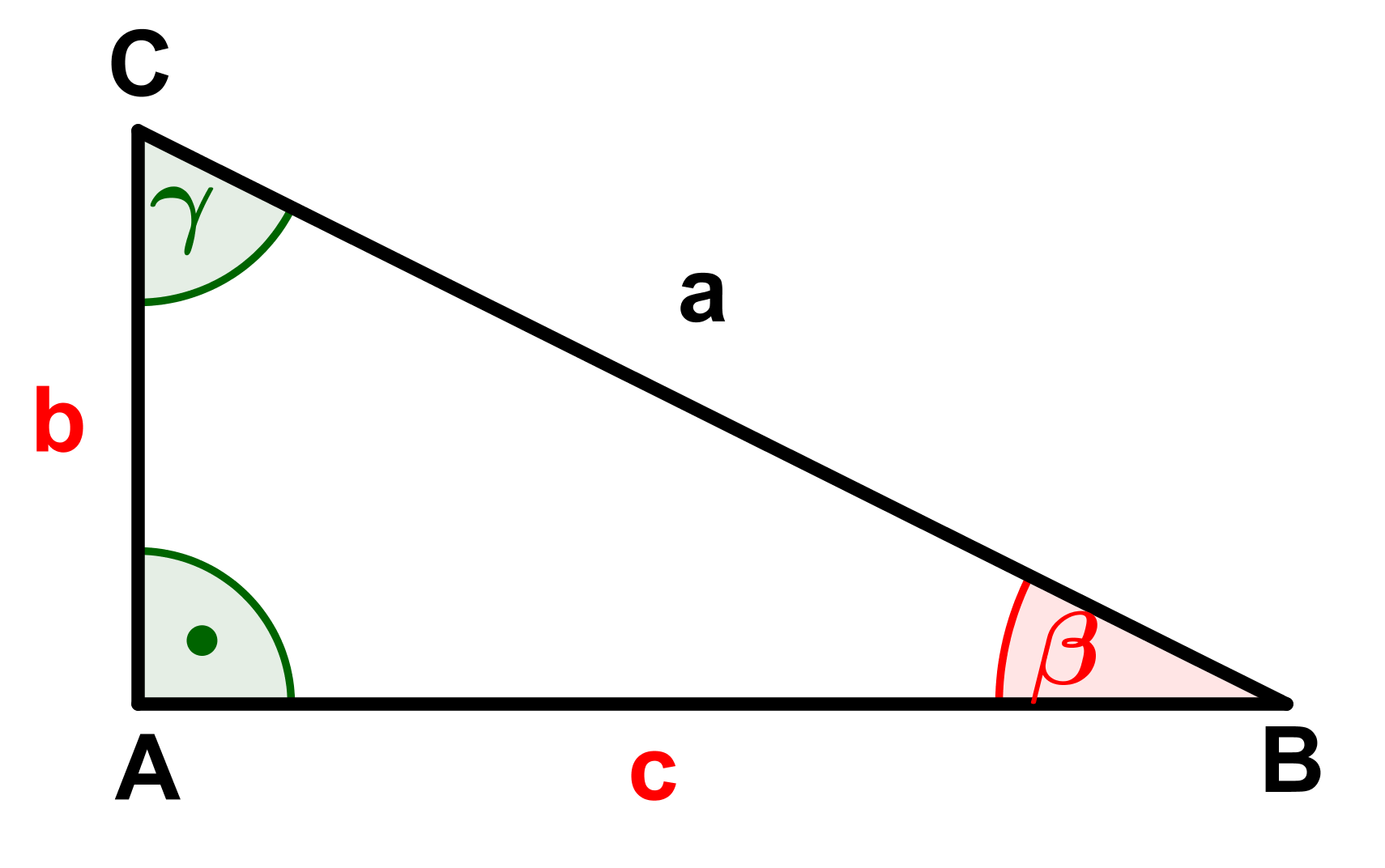
Berechne die fehlenden Seiten und Winkel (rot markiert) der Dreiecke.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 mit Namensnennung von Herrn Rudolf Brinkmann → Was bedeutet das?
Berechne die fehlenden Seiten und Winkel (rot markiert) der Dreiecke.