Dieser Artikel beschäftigt sich mit der Winkelsumme in Dreiecken.
In diesem Artikel geht es um Dreiecke, die man in der Ebene zeichnen kann. Für diese Dreiecke gilt:
Die Summe aller Innenwinkel beträgt immer 180°.
Ein Beispiel für Dreiecke mit einer anderen Winkelsumme findest du am Ende des Artikels.
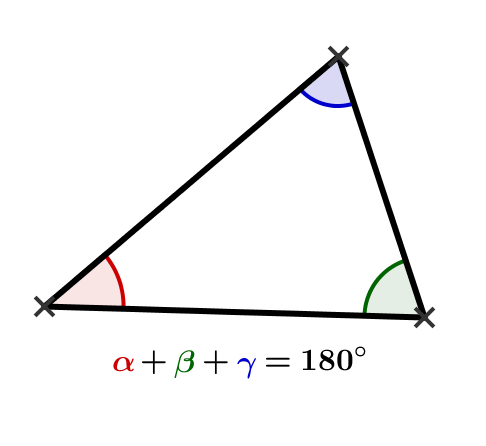
Begründung
Man kann sich diesen Satz zu Hause ganz einfach begreiflich machen:
Man schneidet irgendein Dreieck aus einem Stück Papier oder Pappe.

Anschließend reißt (oder schneidet) man zwei Ecken des Dreiecks ab.

Nun legt man die Ecken an die dritte und stellt fest, dass die drei Ecken zusammen eine gerade Linie bzw. einen gestreckten Winkel (das heißt ) ergeben.

Das funktioniert bei jedem Dreieck mit geraden Seiten!
Begründung mit Winkelsätzen
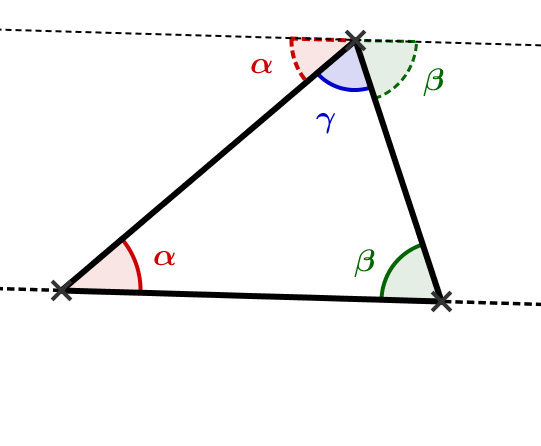
Man kann die Aussage nachvollziehen, indem man sich eine Gerade parallel zu einer der Seiten vorstellt. In der Zeichnung rechts ist das die gestrichelte Linie.
Da diese beiden Geraden parallel sind, kann man die Wechselwinkel zu und neben zeichnen. Man erkennt so, dass gilt.
Du hast noch nicht genug vom Thema?
Hier findest du noch weitere passende Inhalte zum Thema:
