1 Übersicht
Inhalt des Kurses
In diesem Kurs lernst du, wann Dreiecke eindeutig konstruierbar sind. Am Ende kannst du anhand der gegebenen Angaben erkennen, ob das Dreieck eindeutig ist oder nicht.
Vorkenntnisse
Du weißt, was ein Dreieck, eine Strecke und ein Winkel ist.
Du weißt, was Kongruenz bedeutet und hast schonmal etwas von den Kongruenzsätzen von Dreiecken gehört.
Kursdauer
Der Kurs dauert ca. 45min.
2 Motivation 01
Problemstellung:
Die zwei Freundinnen Julia und Lena fahren sehr gerne Skateboard. Julias Papa hat Julia eine Rampe gebaut und jetzt will Lena auch so eine!
Die beiden telefonieren miteinander und Julia erklärt Lena, wie die Rampe aussieht:
"Die Rampe besteht aus einem Brett, das 2m lang ist und das andere ist 1,50m lang. Das 2m-Brett ist vorne, so dass du dann über das 1,5m Brett runter fährst."
Lena zeichnet sich gleich eine Skizze und baut die Rampe:
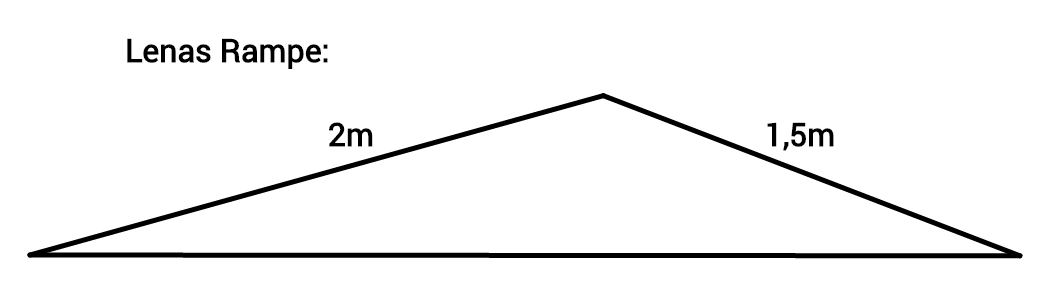
Zwei Wochen später telefonieren die beiden nochmal:
Lena sagt: "Die Rampe ist langweilig! Sie ist überhaupt nicht steil genug!"
Julia: "Meine nicht, sie ist sogar so steil, dass man nur mit viel Anlauf drüber kommt!"
Sie mailen sich die Bilder der Rampen zu, um sie zu vergleichen:
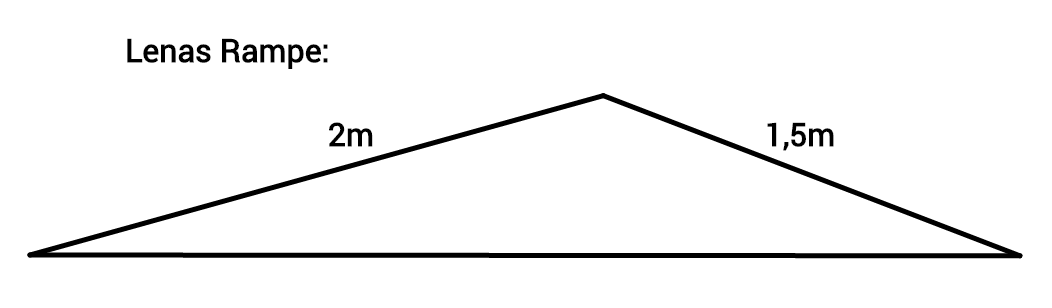
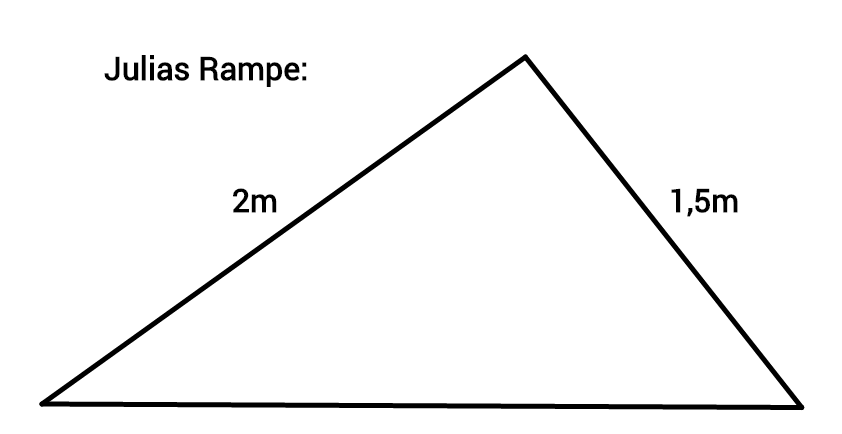
Was ist schiefgelaufen?
Warum haben die beiden unterschiedliche Rampen gebaut, obwohl sie die gleichen Bretter verwendet haben?
3 Motivation 02
Die beiden Rampen sind völlig unterschiedlich, da nur durch die zwei Angaben der Dreiecksschenkel das Dreieck nicht eindeutig ist.
Die Überlegung ist nun: Welche Angaben wären ausreichend gewesen, um das Dreieck eindeutig über das Telefongespräch zu beschreiben?
Diese Fragestellung ist zentral, wenn du aus gegebenen Werten ein Dreieck konstruieren willst.
4 Was ist Konstruieren eigentlich?
Konstruieren bedeutet eine exakte Zeichnung einer Figur anzufertigen und dabei nur die “euklidischen Werkzeuge” Zirkel und Lineal zu verwenden.
Man nutzt dazu immer Schnittpunkte, der gezeichneten Formen. Also Schnittpunkt von Kreis-Kreis, von Gerade-Gerade oder von Kreis-Gerade, um auf die zu bestimmenden Formen zu kommen.
Das Lineal dient dabei nur dazu, um eine gerade Linie zu ziehen. Der Zirkel dient dazu, genaue Strecken abzumessen.
Das besondere am Konstruieren ist, dass die Zeichnungen genauer werden, als wenn man sie mit einem Geodreieck anfertigen würde!
Für die Konstruktion sind einige Größen der Figur angegeben, mit denen man dann die Figur eindeutig konstruieren kann.
Bei einem Dreieck sind die möglichen angegebenen Größen die drei Winkel und die drei Seiten .
Beachte, dass bei Dreiecken die Seite immer gegenüber dem Punkt und dem Winkel liegt.
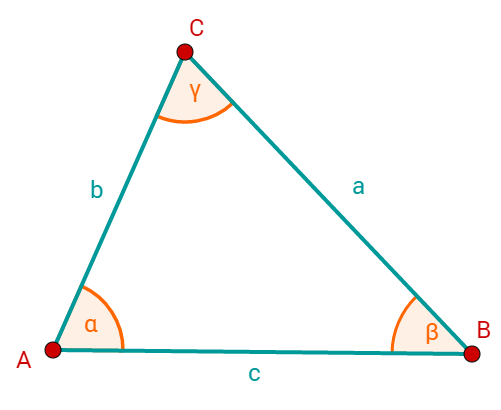
5 Welche Dreiecke kann man konstruieren?
Jetzt kommt die eigentliche Frage. Die Problemstellung ist gleich mit der Frage nach der Eindeutigkeit eines Dreiecks mit angegebenen Größen.
Prinzipiell kannst du jedes beliebige, existierende Dreieck konstruieren.
Die Frage ist also nur: Welche Angaben brauchst du, um ein Dreieck eindeutig konstruieren zu können?
Achtung: Nicht mit allen Angaben ist es möglich, ein Dreieck zu zeichnen!
6 Wie viele Angaben braucht man um ein Dreieck eindeutig konstruieren zu können? 01
Reicht eine Angabe (zum Beispiel eine Seite oder ein Winkel)
Überprüfen dazu, ob immer dasselbe Dreieck herauskommt, wenn du eine Seite/ einen Winkel fest vorgegeben hast:
gegeben: eine Seite, b
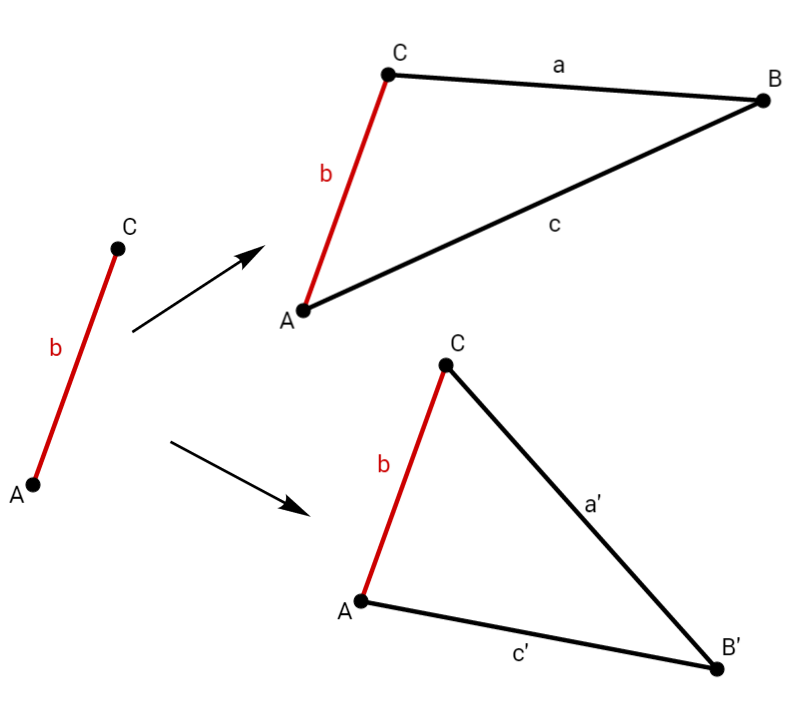
gegeben: ein Winkel,
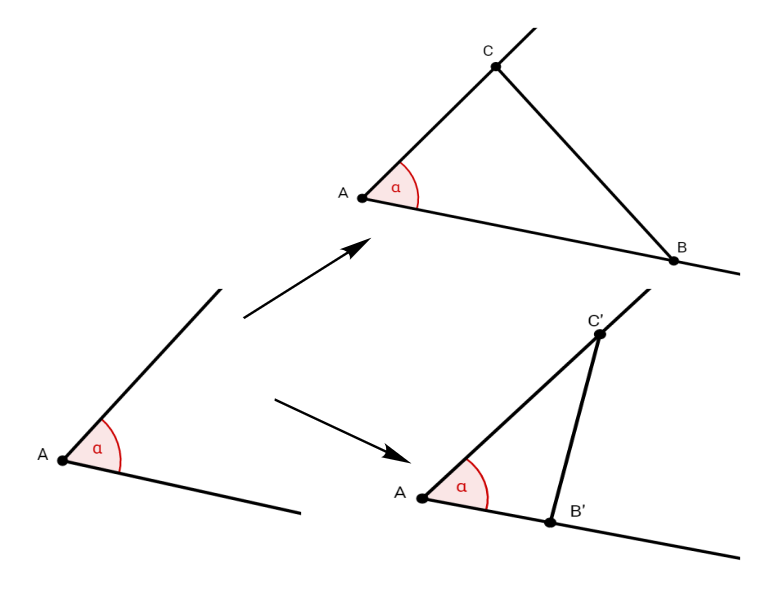
Aus diesen Zeichnungen kannst du eindeutig erkennen, dass aus dieser einen Angabe jeweils beliebig viele unterschiedliche Dreiecke gebildet werden können.
Es reicht also nicht nur eine Angabe, um ein Dreieck eindeutig zu konstruieren!
7 Wie viele Angaben braucht man, um ein Dreieck eindeutig konstruieren zu können? 02
Reichen zwei Angaben aus, um ein Dreieck eindeutig konstruieren zu können?
Überprüfe dazu, ob immer dasselbe Dreieck herauskommt, wenn zwei Angaben fest vorgeben sind.
geg: zwei Seiten (wie bei den Skateboard-Rampen von Lena und Julia)
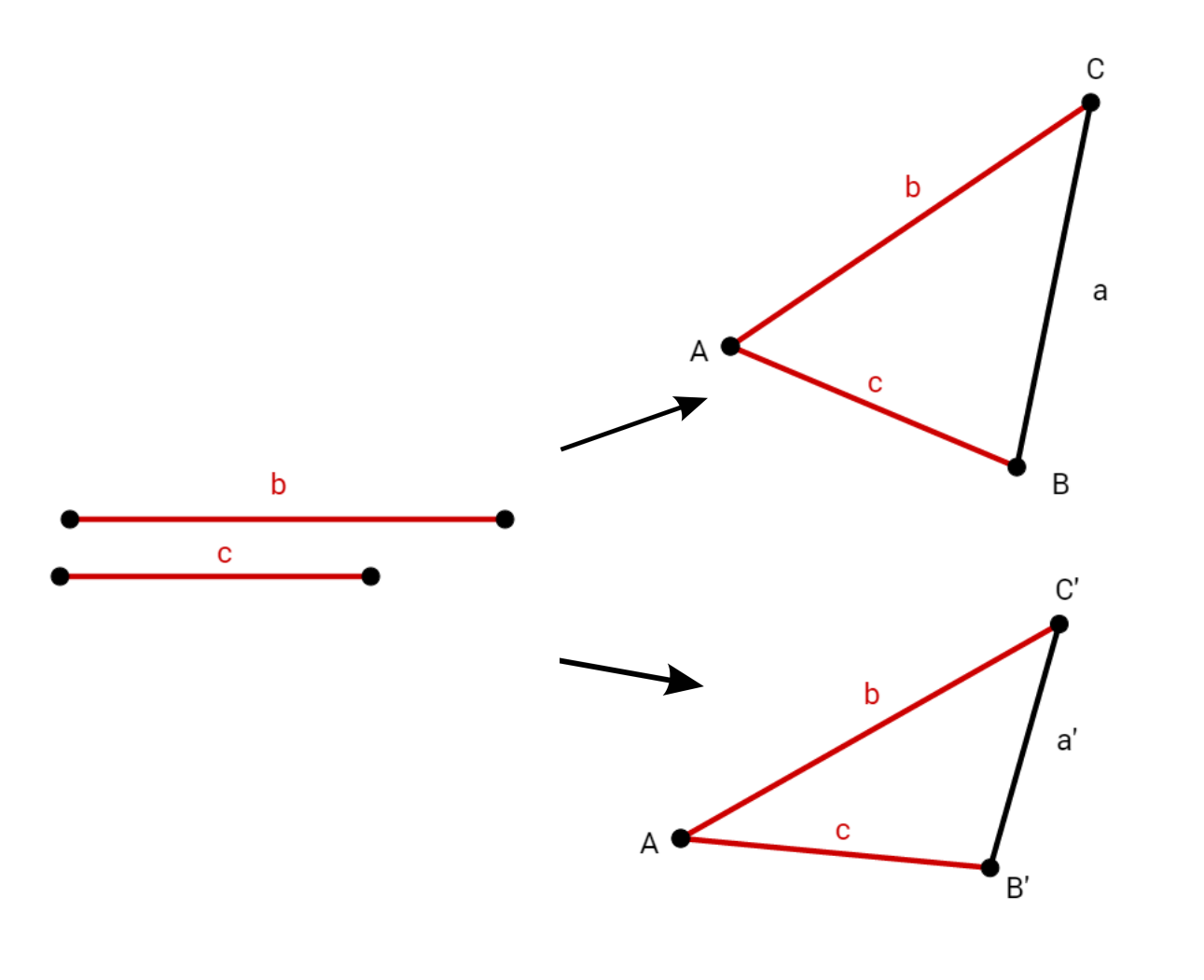
geg: zwei Winkel
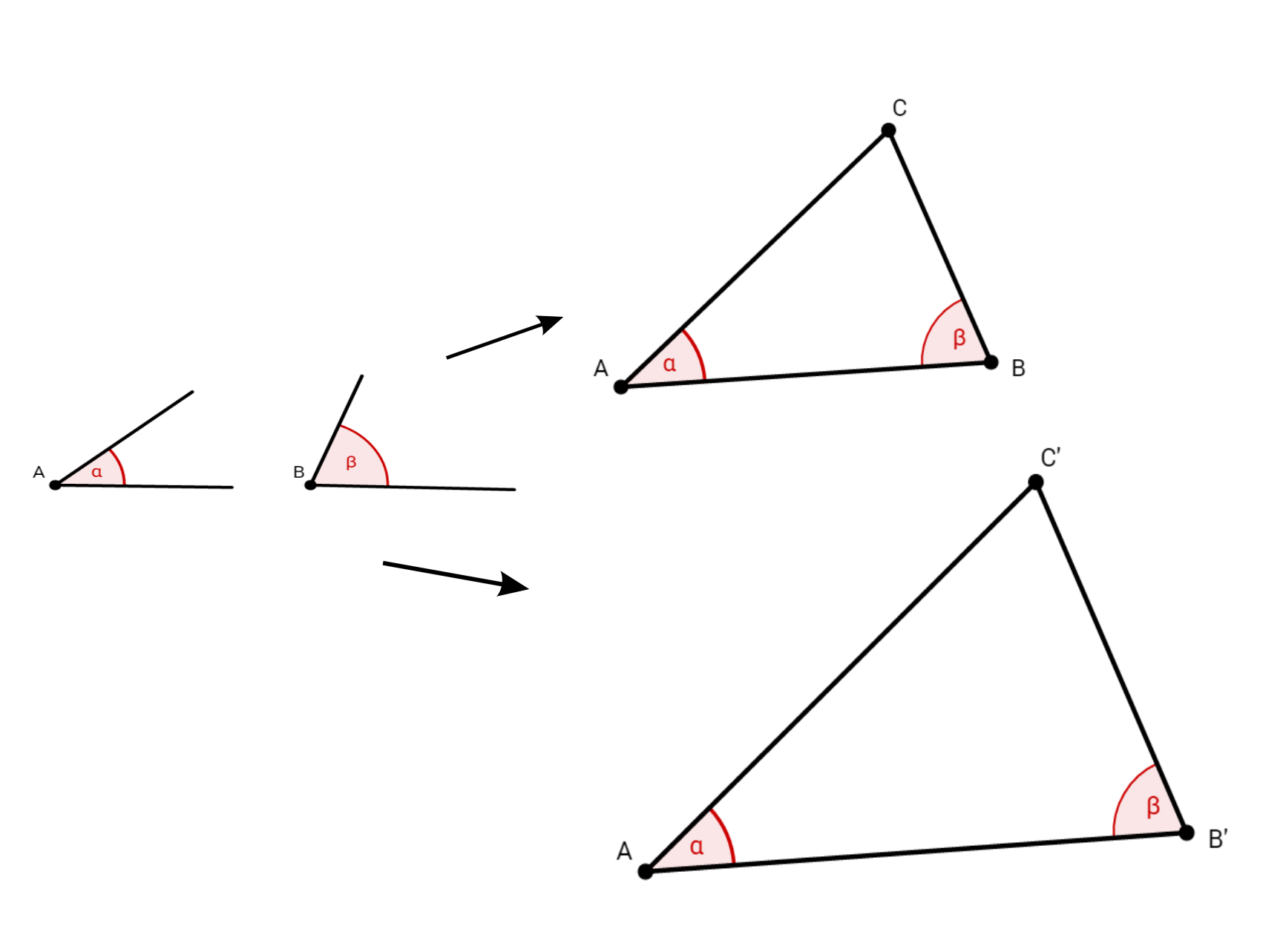
geg: eine Seite, ein Winkel
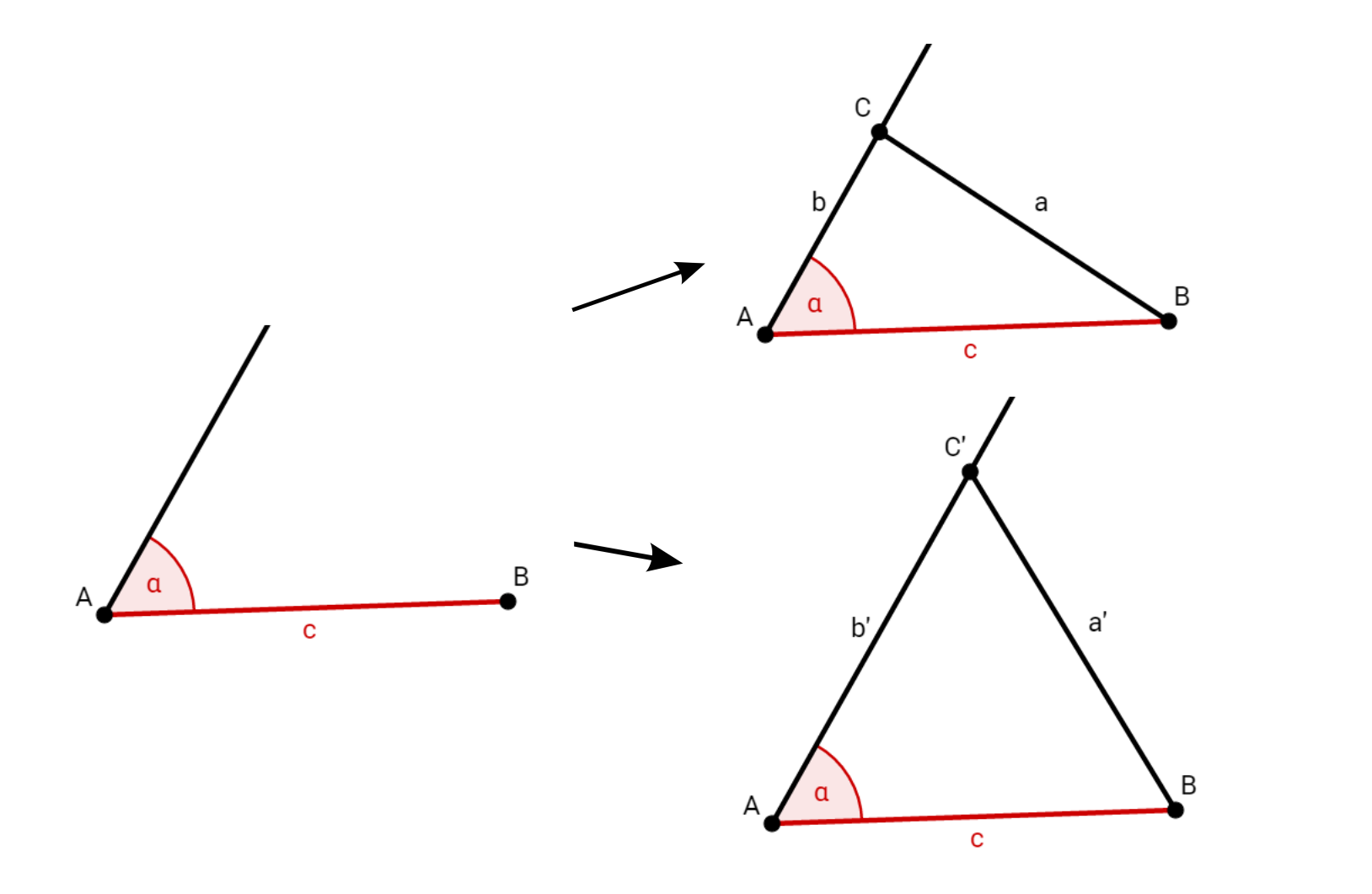
Du kannst eindeutig erkennen, dass du auch aus diesen zwei Angaben jeweils viele unterschiedliche Dreiecke konstruieren kannst.
Es reichen also nicht nur zwei Angaben, um ein Dreieck eindeutig zu konstruieren!
8 Wie viele Angaben braucht man um ein Dreieck eindeutig konstruieren zu können? 03
Mit drei Angaben kannst du einige Dreiecke konstruieren. Allerdings kommt es darauf an, welche Angaben du gegeben hast.
Achtung: Nicht alle Dreiecke, bei denen man drei Angaben hat, existieren überhaupt oder können eindeutig konstruiert werden!
Die Kongruenzsätze für Dreiecke beschreiben, mit welchen Angaben ein Dreieck eindeutig ist. Sobald ein Dreieck eindeutig definiert ist durch die Angaben, kannst du es auch konstruieren.
Auf den folgenden Kursseiten kannst du dir eine Zusammenfassung der Kongruenzsätze ansehen.
9 Zusammenfassung der Kongruenzsätze
Alle Dreiecke die, nach den Kongruenzsätzen, eindeutig sind, können auch konstruiert werden.
Du musst also erst mit einer Skizze überprüfen, welcher Kongruenzsatz gegeben ist.
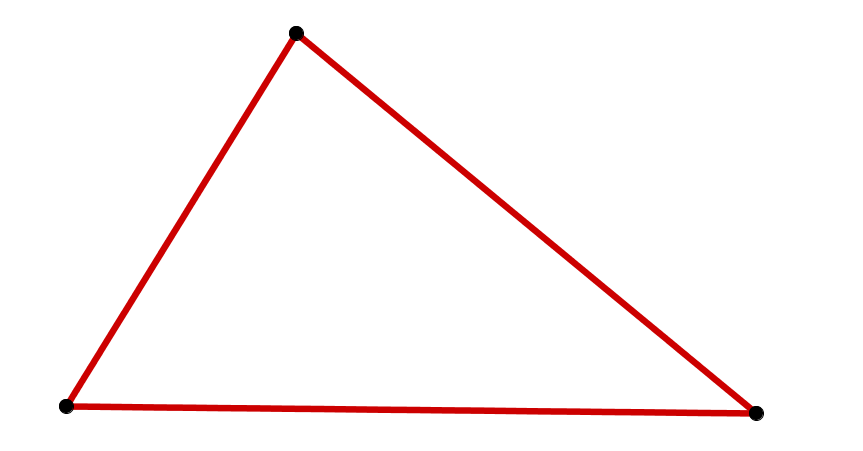
SSS-Satz:
eindeutig konstruierbares Dreieck
Wenn die drei Seiten des Dreiecks gegeben sind, ist das Dreieck eindeutig konstruierbar.
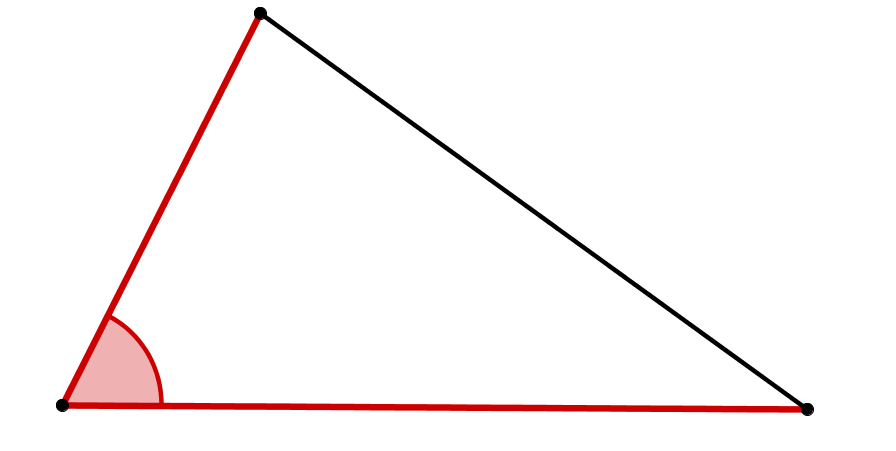
SWS-Satz:
eindeutig konstruierbares Dreieck
Wenn zwei Seiten und der eingeschlossene Winkel gegeben sind, ist das Dreieck eindeutig konstruierbar.
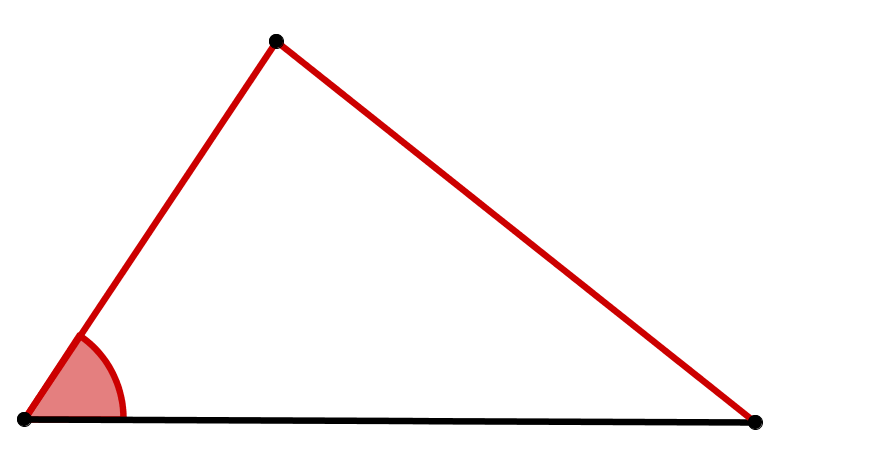
SsW-Satz:
eindeutig konstruierbares Dreieck
Wenn zwei Seiten und der,der längeren Seite gegenüberliegende Winkel gegeben ist, ist das Dreieck eindeutig konstruierbar.
WSW-Satz:
eindeutig konstruierbares Dreieck
Wenn zwei Winkel und die Seite zwischen den Winkeln gegeben ist, ist das Dreieck eindeutig konstruierbar.
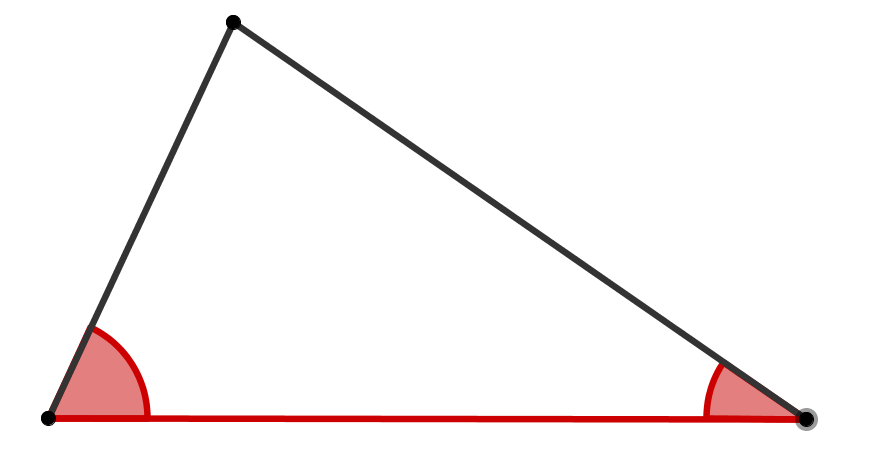
WWW-Satz:
nicht eindeutig konstruierbares Dreieck
Wenn die drei Winkel gegeben sind, ist das Dreieck nicht eindeutig konstruierbar.
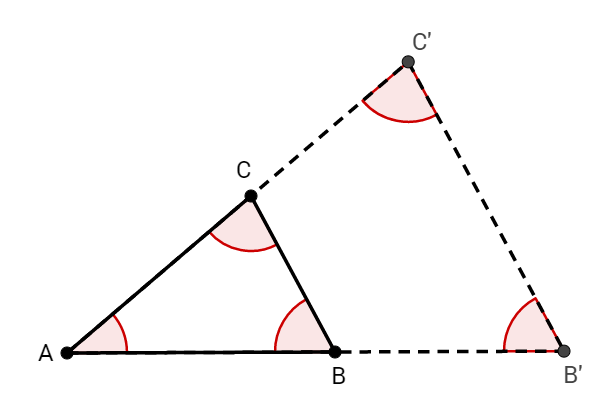
Das Dreieck hat dieselben drei Winkel wie das Dreieck , sie sind aber nicht deckungsgleich und damit nicht kongruent.
sSW-Satz:
nicht eindeutig konstruierbares Dreieck
Wenn zwei Seiten und der,der kleineren Seite gegenüberliegende Winkel gegeben ist, ist das Dreieck .konstruierbar, aber nicht eindeutig konstruierbar
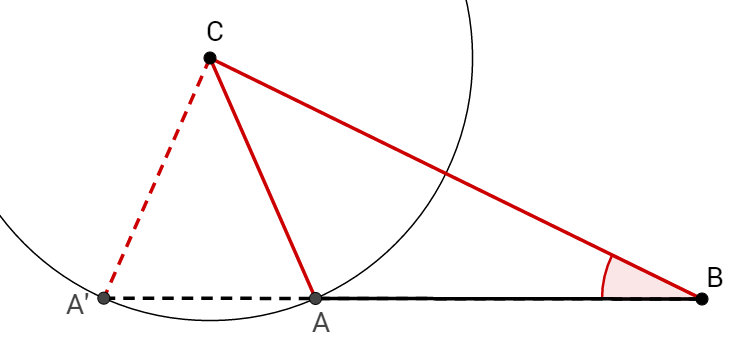
Das Dreieck ABC hat, genau wie A’BC zwei Längen und den Winkel gegenüber der kleineren Seite gegeben. Sie sind aber trotzdem nicht kongruent, da A’B länger als AB ist.
10 Beschränkungen der Kongruenzsätze
Es gibt noch eine Beschränkung des SSS-Satzes.
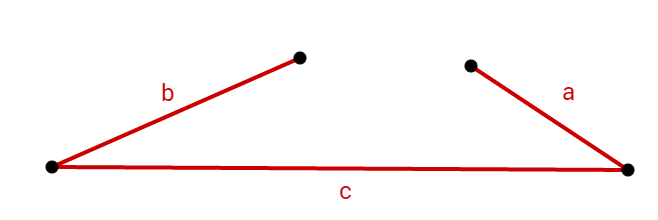
Nicht jedes Dreieck, von dem wir drei Seiten gegeben haben existiert überhaupt. Wenn die zwei kleinen Seiten zusammen kleiner sind als die dritte, große Seite, kann man aus diesen Seiten kein Dreieck bilden.
Ist
existiert das Dreieck nicht!
Prüfe das, bevor du anfängst zu konstruieren!
11 Übung - Ist das Dreieck konstruierbar?
Laden
12 Übung: Rampen-Bau
Laden
13 Dreiecke konstruieren
Lehrgang Klasse 7
