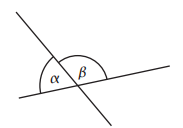
Die zwei Geraden schneiden sich in einem Punkt, wobei um 80°größer als ist.
Gib das Winkelmaß an.
Dieses Werk steht unter der freien Lizenz
CC BY-SA 4.0 → Was bedeutet das?
Die zwei Geraden schneiden sich in einem Punkt, wobei um 80°größer als ist.
Gib das Winkelmaß an.
